Дифференциальные зависимости при прямом поперечном изгибе

Построение эпюр поперечных сил и изгибающих моментов су­щественно упрощается при использовании дифференциальных зави­симостей между изгибающим моментом, поперечной силой и интен­сивностью равномерно распределенной нагрузки (теорема Журавского):

Поперечная сила равна производной от изгибающего момента по длине балки:

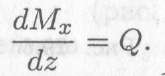
Интенсивность равномерно распределенной нагрузки равна про­изводной от поперечной силы по длине балки:

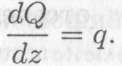
Из выше указанного следует:

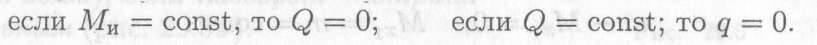
Контрольные вопросы

1. Какую плоскость называют силовой?

2. Какой изгиб называют прямым? Что такое косой изгиб?

3. Какие силовые факторы возникают в сечении балки при чистом изгибе?

4. Какие силовые факторы возникают в сечении при поперечном изгибе?

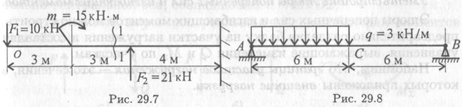
5. Определите поперечную силу и изгибающий момент в сечении 1-1 (рис. 29.7). Расстояние сечения от свободного конца балки 5 м.

6. Определите реакцию в опоре В.

7. Определите величину поперечной силы и изгибающего момента в сечении С, использовав схему балки (рис. 29.8).

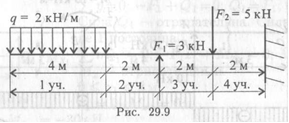
8. Определите участок чистого изгиба (рис. 29.9).

ЛЕКЦИЯ 30

Тема 2.6. Изгиб. Построение эпюр поперечных сил и изгибающих моментов. Основные правила построения эпюр

Знать порядок построения и контроля эпюр поперечных сил и изгибающих моментов.

Уметь строить эпюры поперечных сил и изгибающих моментов.

Эпюры поперечных сил и изгибающих моментов можно строить, предварительно разделив балку на участки нагружения и составляя уравнения, выражающие изменения Q и М_х по участкам.

Напомним, что границы участков нагружения — это сечения, в которых приложены внешние нагрузки.

Примеры решения задач

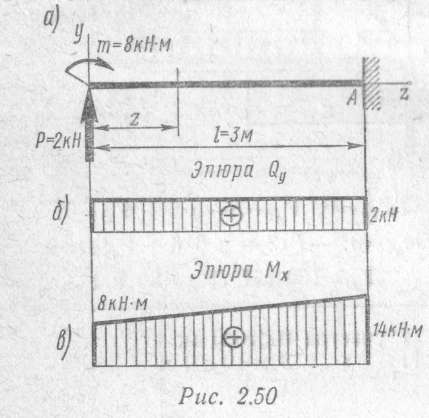Пример 1. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 2.50, а.

Решение

При построении эпюр для балок с одним защемленным концом можно не определять опорные реак­ции. Проводя сечение, будем рассматривать равновесие той части, к которой приложены только внешние (актив­ные) силы. Для балки по рис. 2.50, а такой частью будет левая.

Рассматривая равнове­сие левой отсеченной час­ти балки, выразим попе­речную силу и изгиба­ющий момент в произволь­ном сечении

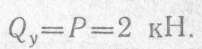
Поперечная сила положи­тельна, так как внешняя нагрузка направлена сле­ва от сечения вверх, Q_y постоянна на всем протяжении балки. Эпюра поперечных сил построена на рис. 2.50, б.

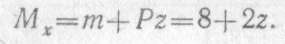
Оба слагаемых, входящих в выражение изгибающего момента, положительны, так как соответствующие внеш­ние силы изгибают балку выпуклостью вниз. Изгибающий момент выражается линейной функцией от абсциссы се­чения z. Поэтому для построения этой эпюры достаточно найти значения изгибающего момента только в двух се­чениях балки:

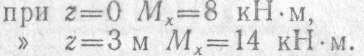
Эпюра моментов показана на рис. 2.50, в.

Пример 2. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 2.52,а.

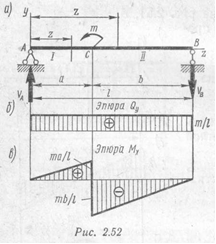Решение

Определяем опорные реакции. Реакция V _А направлена вверх, V_B — вниз, так как эти реакции об­разуют пару сил, уравновешивающую пару с моментом т. Составляя суммы моментов относительно опорных точек Л и В, находим:

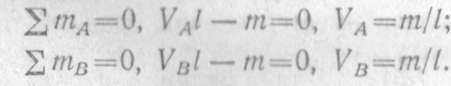
Для проверки опорных реакций составляем сумму проекций на вертикальную ось:

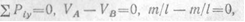
следовательно, реакции вычислены правильно.

Балка имеет два участка I, II. Проводим произволь­ное сечение на участке I на расстоянии z от опоры А и рассматриваем левую отсеченную часть. Поперечная сила на этом участке постоянна, равна реакции V_А и положи­тельна, так как эта реакция направлена вверх и прило­жена слева от сечения.

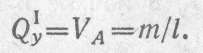
Изгибающий момент в произвольном сече­нии участка I

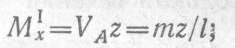
Момент положите­лен, так как сила V_A изгибает балку выпук­лостью вниз.

В произвольном се­чении участка II попе­речная сила будет та­кой же, как на участ­ке I:

Изгибающий момент в произвольном сечении участ­ка II

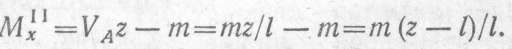
Вычислим изгибающий момент в начале и в конце участка II:

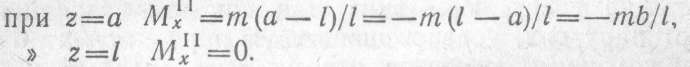
Эпюры Q_y и М_х показаны на рис. 2.52, б, в. В сече­нии, где приложен сосредоточенный момент,в эпюре из­гибающих моментов имеется скачок, равный по величине внешнему моменту.

Пример 3. Для балки, изображенной на рис. 2.53, а, построить эпюры Q_y и М_г.

Решение

Определяем опорные реакции V_A и V_B:

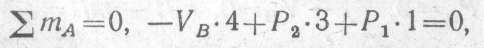
откуда

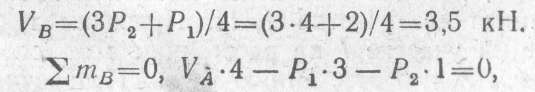
Откуда

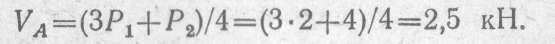
Составляем проверочное уравнение:

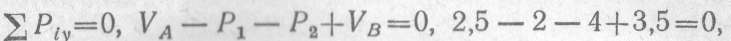
следовательно, опорные реакции определены верно.

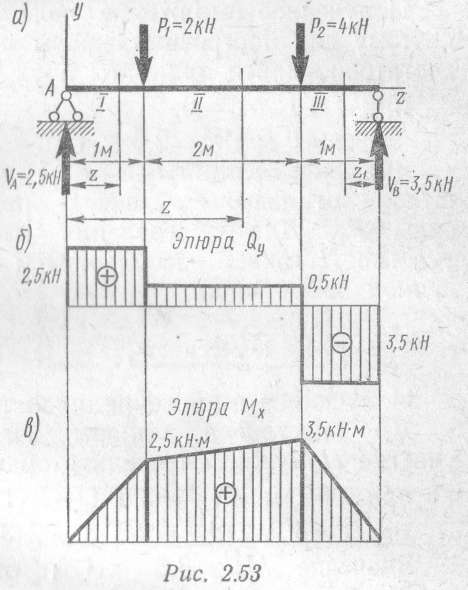Валка имеет три участка I, II, III (см. рис. 2.53, а): участок I — от опоры А до силы Р₁ (0 < z < l м), уча­сток II — от силы Р₁ до силы Р₂ (1 м << z < 3 м), участок III — от силы Р₂ до опоры В. На этом участке абсциссу удобнее отсчитывать не слева, а справа, т. е. от опоры В ( 0 < z₁ < 1 м).

Поперечная сила в произвольном сече­нии участка I

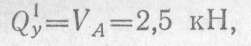
в произвольном сече­нии участка II

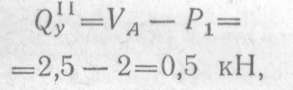
в произвольном сечении участка III

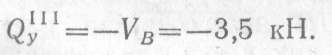
Если рассматривать левую отсеченную часть балки, то получим то же самое значение поперечной силы:

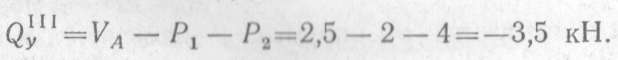
В последнем случае вычисления оказались более гро­моздкими, так как к левой части балки приложено три силы, а к правой — только одна. В пределах каждого участка поперечная сила постоян­на. По вычисленным значениям с соблюдением правила знаков эпюра Q_y построена на рис. 2.53, б. Эпюра имеет скачки под сосредоточенными силами V_A, P₁, Р₂, V_B, величина и направление скачка соответствуют величине и направлению внешней силы.

Переходим к построению эпюры изгибающих момен­тов. Берем сечение в пределах участка /; слева от него расположена одна сила — опорная реакция V_A. Изгибаю­щий момент в произвольном сечении участка I

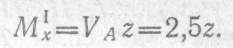
Полученное выражение является уравнением прямой, поэтому для построения эпюры моментов на этом участке достаточно найти ординаты двух точек:

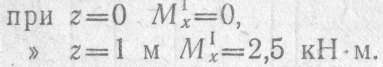
Значение ординаты М_х = 2,5 кН-м в выбранном мас­штабе откладываем вверх под точкой приложения силы P_v. Для определения изгибающего момента на участке II также рассматриваем равновесие левой отсе­ченной части балки:

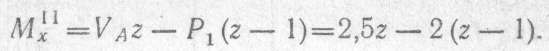
Полученное выражение является уравнением прямой.

Для построения эпюры изгибающих моментов на участке II нужно определить ординаты в двух точках:

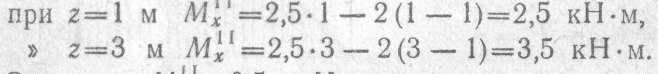
Значение M_x^II = 3,5 кН-м откладываем вверх под силой Р₂ и соединяем с уже построенной ординатой в сечении под силой P₁.

На участке III целесообразно рассмотреть правую часть балки, так как к ней приложено меньше сил, чем к левой:

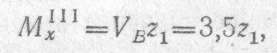
где z₁ отчитывается от опоры В и изменяется в преде­лах от 0 до 1 м;

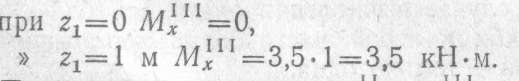
Под силой Р₂ значение M_x^II = M_x^11I, что подтверждает правильность решения.

Эпюра изгибающих моментов изображена на рис. 2.53, в.

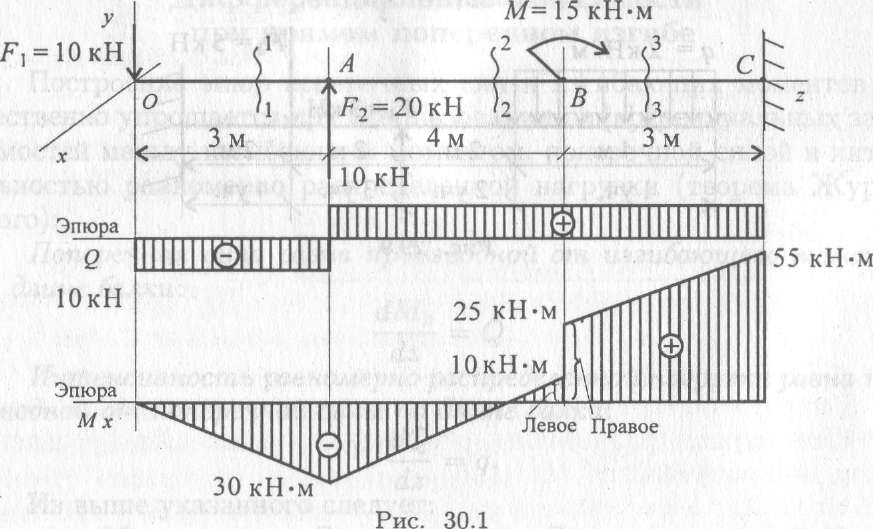Пример 4. На балку действуют сосредоточенные силы и мо­мент (рис. 30.1). Построить эпюры поперечных сил и изгибающих моментов.

Решение

Последовательно по участкам нагружения рассматриваем внут­ренние силовые факторы в сечениях. Силовые факторы определяем из условий равновесия отсеченной части. Для каждого участка за­писываем уравнения внутренних силовых факторов.

Используем известные правила:

— поперечная сила численно равна алгебраической сумме про­екций внешних сил на ось Оу,

— изгибающий момент численно равен алгебраической сумме моментов внешних сил, действующих на отсеченную часть, относи­тельно нейтральной оси, совпадающей с осью Ох;

— принятые знаки поперечных сил и изгибающих моментов (рис. 30.2):

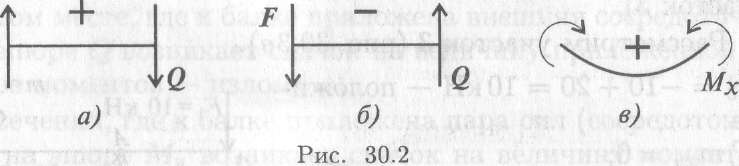
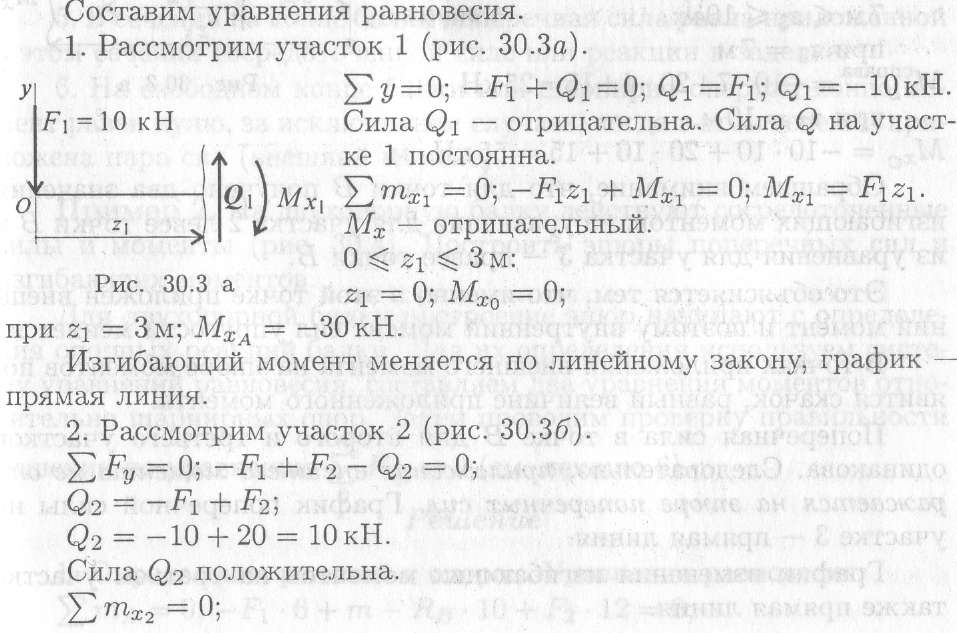
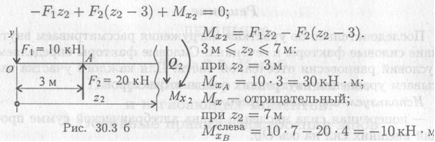
Знак сменился; М_Хв слева от сечения В — положительный.

Поперечнуюсилу и изгибающий момент можно определять сра­зу из зависимостей

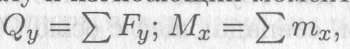
не составляя уравнения равновесия участка.

Знак каждого из слагаемых этих уравнений определяем отдель­но (участок 3).

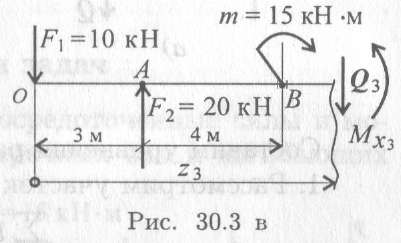3. Рассмотрим участок 3 (рис. 30.Зе).

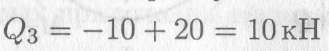— положи­тельна.

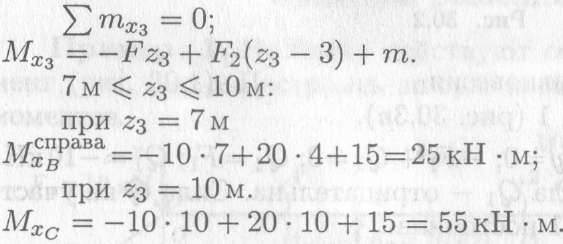
Обращаем внимание, что для точки В получено два значения изгибающих моментов: из уравнения для участка 2 левее точки В и из уравнения для участка 3 — правее точки В.

Это объясняется тем, что именно в этой точке приложен внеш­ний момент и поэтому внутренний момент сил упругости меняется.

В точках приложения внешнего момента на эпюре моментов по­явится скачок, равный величине приложенного момента.

Поперечная сила в точке В для второго и третьего участков одинакова. Следовательно, приложение внешнего момента не от­ражается на эпюре поперечных сил. График поперечной силы на участке 3 — прямая линия.

График изменения изгибающих моментов на третьем участке также прямая линия.

4. Построение эпюр. Порядок построения эпюр остается преж­ним: масштабы эпюр выбираются отдельно, исходя из значений мак­симальных сил и моментов.

Графики обводятся толстой основной линией и заштриховыва­ются поперек. На графиках указываются значения поперечных сил, изгибающих моментов и единицы измерения.

Правила построения эпюр (рис. 30.1 и 30.4):

— Для участка, где отсутствует распределенная нагрузка, попе­речная сила постоянна, а изгибающий момент меняется по линейно­му закону.

— В частном случае, когда поперечная сила на участке равна ну­лю, изгибающий момент постоянен (чистый изгиб), график — прямая линия, параллельная продольной оси (на рис. 30.1 отсутствует).

— В том месте, где к балке приложена внешняя сосредоточенная сила, на эпюре Q возникает скачок на величину приложенной силы, а на эпюре моментов — излом.

— В сечении, где к балке приложена пара сил (сосредоточенный момент), на эпюре М_и возникает скачок на величину момента этой пары. Поперечная сила при этом не изменяется.

— В сечении на конце балки поперечная сила равна приложенной в этом сечении сосредоточенной силе или реакции в заделке.

— На свободном конце балки или шарнирно опертом конце мо­мент равен нулю, за исключением случаев, когда в этом сечении при­ложена пара сил (внешний момент).

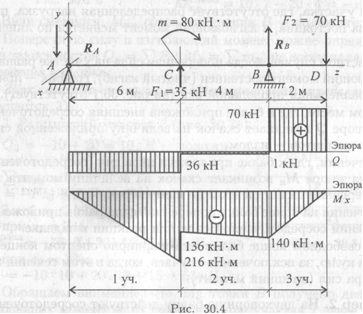
Пример 5. На двухопорную балку действуют сосредоточенные силы и моменты (рис. 30.4). Построить эпюры поперечных сил и изгибающих моментов.

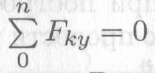Для двухопорной балки построение эпюр начинают с определе­ния опорных реакций балки. Для их определения используем систе­му уравнений равновесия, составляем два уравнения моментов отно­сительно шарнирных опор. Затем проводим проверку правильности решения по уравнению (см. лекцию 6).

Решение

5. Определение реакций в опорах.

Уравнения равновесия:

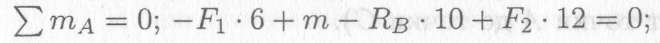
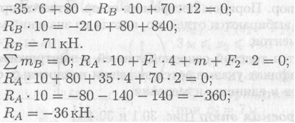
Реакция в опоре направлена в обратную сторону.

Проверка: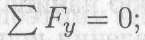

Реакции определены верно.

2. Для упрощения расчетов при построении эпюр поперечных сил и изгибающих моментов можно провести расчет по характерным точкам без составления уравнений.

Для этого используют известные связи между поперечной силой и изгибающим моментом и правила построения эпюр.

Участок 1 (от точки А до точки С).

В точке А приложена реакция Ra, направленная вниз. Попереч­ная сила на участке постоянна:

Момент в точке А равен нулю.

Точка С (слева). Приложена внешняя сила F₁ = 35кН, направ­ленная вверх, — здесь возникнет скачок вверх на величину 35 кН. Момент в точке С (слева) может быть рассчитан по известной зави­симости

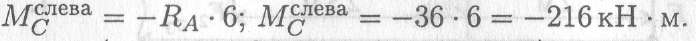
Участок 2 (от точки С справа до точки В).

Поперечная сила в точке С (справа) равна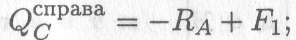

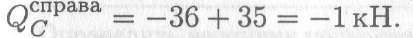
В точке С приложена внешняя пара сил с моментом 80кН-м, следовательно, здесь проявляется скачок на величину приложенного момента:

.

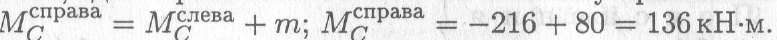
Поперечная сила на втором участке постоянна: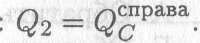

Момент в точке В определяется по зависимости М_в = -Ra * 10 + F₁ * 4 + m; М_в = -36 • 10 + 35 • 4 + 80 = -140кН-м.

Справа и слева от точки В момент имеет одинаковые значения.

Участок 3 (от точки В (справа) до точки D).

В точке В приложена внешняя сила R_B. Здесь появляется ска­чок на величину 71 кН,

Q_B = — 1 + 71 = 70 кН.

Дальше по участку поперечная сила не изменяется. Момент в точке D равен нулю, т. к. здесь не приложена внешняя пара сил: M_D = 0.

Рассмотрение поперечных сил и изгибающих моментов можно было провести слева направо или справа налево.

По полученным значениям сил и моментов строим эпюры (эпю­ры под схемой вала, рис. 30.4).

Контрольные вопросы и задания

1. Определите величины поперечных сил в сечении 1 и в сече­нии 2 (рис. 30.5).

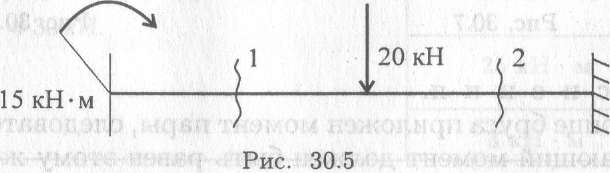
1. Напишите формулу для расчета изгибающего момента в се­чении 3 (рис. 30.6).

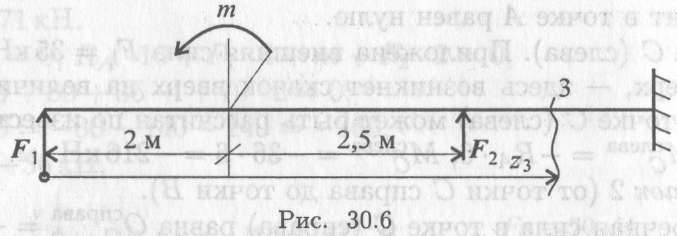
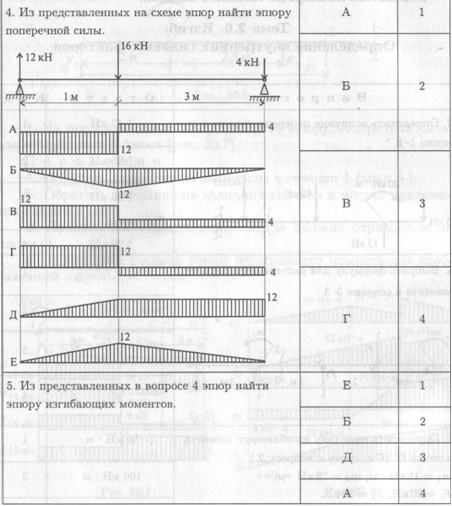
1. Из представленных эпюр выберете эпюру поперечной силы для изображенной балки (рис. 30.7).

Пояснения.

А. Обратить внимание на знак силы в сечении 1 (знак +).

Б. Обратить внимание на величину скачков в местах приложе­ния внешних сил.

В. Приложение момента пары сил не должно отражаться на эпюре Q.

1. По рис. 30.8 выбрать эпюру изгибающего момента для изоб­раженной на рис. 30.7 балки.

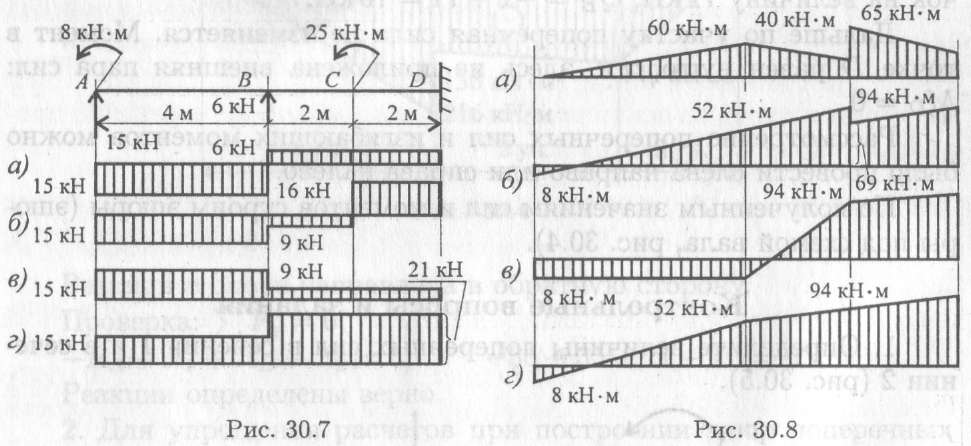
Пояснения.

А. На конце бруса приложен момент пары, следовательно, в этом месте изгибающий момент должен быть равен этому же значению.

Б. Обратить внимание на знак момента в сечении 1.

В. В точке А приложена также и сила, поэтому линия, очертив­шая эпюру, должна быть наклонной.

5. Ответьте на вопросы тестового задания.

Тема 2.6. Изгиб. Определение внутренних силовых факторов

ЛЕКЦИЯ 31