Алгоритм равномерного поиска точки минимума

Алгоритм поиска минимума функции сводится к выполнению следующих этапов.

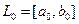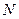1 этап. Задается начальный интервал неопределенности и - количество вычислений функции.

2 этап. Вычислить точки , равноотстоящие друг от друга.

3 этап. Вычислить значения функции в 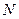найденных точках .

4 этап. Среди точек , найти такую, в которой функция принимает наименьшее значение .

5 этап. Точка минимума принадлежит интервалу , на котором в качестве приближенного решения может быть выбрана точка .

Для оценки сходимости используется характеристика относительного уменьшения начального интервала неопределенности .

Примечание. Если разбиение интервала 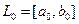производится на 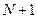равные части (метод перебора), то этапы 2-4 выглядят следующим образом

2 этап. Вычислить точки , равноотстоящие друг от друга.

3 этап. Вычислить значения функции в 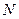найденных точках .

4 этап. Среди точек , найти такую, в которой функция принимает наименьшее значение .

Погрешность нахождения точки минимума методом перебора не превосходит .

Метод деления интервала пополам

Метод относится к последовательным стратегиям и позволяет исключать из дальнейшего рассмотрения на каждой итерации в точности половину текущего интервала неопределенности. Алгоритм уменьшения интервала основан на анализе величин функции в трех точках, равномерно распределенных на текущем интервале (делящих его на четыре равные части). Поиск заканчивается, если длина текущего интервала неопределенности меньше заданной величины.

Алгоритм поиска точки минимума методом деления интервала пополам

Алгоритм поиска минимума функции сводится к выполнению следующих этапов.

1 этап. Задается начальный интервал неопределенност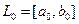и и 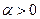- требуемая точность.

2 этап. Задать .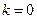

3 этап. Вычислить среднюю точку .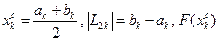

4 этап. Вычислить точки 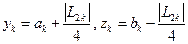, которые с 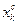делят интервал 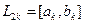на четыре равные части, и функции .

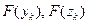5 этап. Если 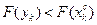, исключить интервал 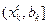, приняв 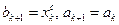. Средней точкой нового интервала становится точка .

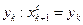Перейти на этап 7.

Если 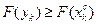, перейти на этап 6.

6 этап. Если 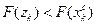, исключить интервал 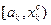, приняв 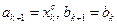. Средней точкой нового интервала становится точка .

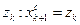Перейти на этап 7.

Если 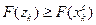, исключить интервалы 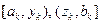, приняв 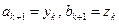. Средней точкой нового интервала останется точка .

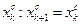7 этап. Вычислить 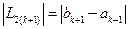и проверить условие окончания:

Если 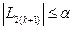, то процесс поиска завершается и 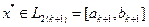. В качестве приближенного решения принимают середину последнего интервала .

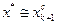Если 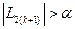, то принять 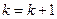и перейти к этапу 4.

Для оценки сходимости метода используется характеристика относительного уменьшения начального интервала неопределенности 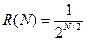, где 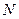количество вычислений функции.

Метод дихотомии

Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и требуемая точность. Алгоритм опирается на анализ значений функции в двух точках. Для их нахождения текущий интервал неопределенности делится пополам и в обе стороны от середины откладывается по , где малое положительное число. Поиск заканчивается, если длина текущего интервала неопределенности меньше заданной величины.