Численные методы одномерной минимизации

Лабораторная работа № 1

Тема: Численные методы одномерной минимизации.

Цель работы: Приобретение практических навыков для решения задач одномерной минимизации численными методами.

Постановка задачи

Требуется найти безусловный минимум функции одной переменной , то есть, такую точку , что .

Поставленная задача может быть решена с помощью необходимых и достаточных условий безусловного экстремума. Однако, во многих практических случаях найти производные от заданной функции не представляется возможным. Поэтому решение задач одномерной оптимизации численными методами является актуальным при изучении методов оптимизации.

Численные методы одномерной минимизации

К основным численным методам одномерной минимизации относят:

- метод равномерного поиска;

- метод деления отрезка пополам;

- метод дихотомии;

- метод золотого сечения;

- метод Фибоначчи;

- метод квадратичной интерполяции и др.

Метод равномерного поиска

Метод относится к пассивным стратегиям поиска точки экстремума. Задается начальный интервал неопределенности 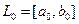и количество вычислений 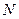. Вычисления производятся в 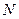равноотстоящих друг от друга точках. При этом интервал делится на 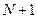равных интервалов. Путем сравнения величин находится точка , в которой значение функции наименьшее. Искомая точка считается заключенной в интервале .

Алгоритм равномерного поиска точки минимума

Алгоритм поиска минимума функции сводится к выполнению следующих этапов.

1 этап. Задается начальный интервал неопределенност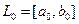и и 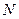- количество вычислений функции.

2 этап. Вычислить точки , равноотстоящие друг от друга.

3 этап. Вычислить значения функции в 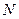найденных точках .

4 этап. Среди точек , найти такую, в которой функция принимает наименьшее значение .

5 этап. Точка минимума принадлежит интервалу , на котором в качестве приближенного решения может быть выбрана точка .

Для оценки сходимости используется характеристика относительного уменьшения начального интервала неопределенности .

Примечание. Если разбиение интервала 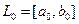производится на 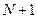равные части (метод перебора), то этапы 2-4 выглядят следующим образом

2 этап. Вычислить точки , равноотстоящие друг от друга.

3 этап. Вычислить значения функции в 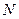найденных точках .

4 этап. Среди точек , найти такую, в которой функция принимает наименьшее значение .

Погрешность нахождения точки минимума методом перебора не превосходит .

Метод дихотомии

Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и требуемая точность. Алгоритм опирается на анализ значений функции в двух точках. Для их нахождения текущий интервал неопределенности делится пополам и в обе стороны от середины откладывается по , где малое положительное число. Поиск заканчивается, если длина текущего интервала неопределенности меньше заданной величины.

Метод золотого сечения

В методе золотого сечения в качестве двух внутренних точек выбираются точки золотого сечения.

Точка производит золотое сечение, если отношение длины всего отрезка к большей части равно отношению большей части к меньшей части. На отрезке 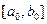имеются две симметричные относительно его концов точк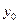и и :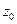

.

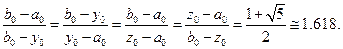Точка 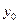производит золотое сечение отрезка 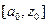, а точка 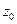- отрезка .

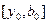Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и требуемая точность. Алгоритм опирается на анализ значений функции в двух точках. В качестве точек вычисления функции выбираются точки золотого сечения. На каждой итерации, кроме первой, требуется только одно новое вычисление функции. Поиск заканчивается, если длина текущего интервала неопределенности меньше заданной величины.

Метод Фибоначчи

В методе Фибоначчи реализована последовательная стратегия, обеспечивающая максимальное гарантированное сокращение интервала неопределенности при заданном количестве вычисления функции. Эта стратегия опирается на числа Фибоначчи, определяемые по формуле

.

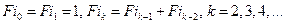Последовательность чисел Фибоначчи имеет вид 1,1,2,3,5,8,13,23,34,55,89,144,233,.. .

Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и количество вычислений функции. Алгоритм опирается на анализ значений функции в двух точках. Точки вычисления функции находятся с использованием последовательности из 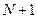чисел Фибоначчи. На каждой итерации, кроме первой, требуется только одно новое вычисление функции. Поиск заканчивается, если длина текущего интервала неопределенности меньше заданной величины.

Варианты заданий

Варианты заданий приведены в таблице.

Таблица. Варианты заданий

№	F(X) =	Тип экстремума	Исходный интервал	Погрешность
		max	[4; 9]	0.02
		min	[-1; 0]	0.005
		max	[4; 9]	0.02
		min	[-1; 0]	0.005
		min	[0.5; 1]	0.001
		min	[-2; 0]	0.01
		min	[-1.5; 3]	0.01
		min	[1.3; 3.0]	0.01
		max	[0; 3]	0.02
		min	[0; 2.5]	0.02
		max	[0.8; 2.0]	0.008
		min	[0; 1.5]	0.01
		min	[1; 3]	0.012
		max	[0; 3]	0.02
		max	[-1; 0.5]	0.005
		min	[0; 2]	0.01
		min	[0; 2]	0.01
		min	[-1; 0]	0.002
		min	[0; 1]	0.005
		min	[-1; 1]	0.01
		max	[2; 6]	0.02
		min	[0; 2]	0.01
		min	[0.5; 2]	0.01
		min	[0; 1.5]	0.01
		min	[0.5; 2]	0.005
		min	[0; 2]	0.005

Задание

1. Составить блок-схемы алгоритмов поиска точки экстремума заданной функции.

2. Построить график функции для выбора границ первоначального интервала.

3. По разработанным алгоритмам составить программы поиска минимума функции.

4. Найти координаты и значение функции в точке минимума всеми методами.

5. Найти точное значение координаты точки минимума, используя необходимые и достаточные условия экстремума.

6. Проанализировать полученные результаты и сделать выводы по достигнутой точности и количеству вычислений функции.

7. Дать письменные ответы на контрольные вопросы.

Контрольные вопросы

1. В чем состоит необходимое и достаточное условие экстремума одномерной функции?

2. В чем заключается условие унимодальности функции и как это условие используется?

3. Понятие выпуклой функции.

4. Как найти экстремум функции?

5. Как ведет себя производная в области точки экстремума?

6. Верно ли утверждение, что всякая выпуклая непрерывная на отрезке функция является на этом отрезке унимодальной?

7. Как ведет себя касательная к выпуклой функции? Поведение ее в области экстремума?

8. Можно считать, что глобальный минимум является локальным? А наоборот?

9. В чем различие между пассивным и последовательным поиском?

10. Что называют интервалом неопределенности в задачах одномерной оптимизации?

11. В чем состоит метод дихотомии?

12. Какие трудности возникают в методе квадратичной аппроксимации?

13. Каким образом сравнивают эффективность методов прямого поиска?

Содержание отчета

1. Цель работы.

2. Формулировка задачи.

3. Блок-схемы алгоритмов поиска минимума.

4. Графическое представление функции.

5. Листинги программ.

6. Результаты вычислений.

7. Сравнительная характеристика методов.

8. Выводы.

ЛИТЕРАТУРА

1. Лесин В.В., Лисовец Ю.П. Основы методов оптимизации: Учебное пособие. – СПб.: Издательство «Лань», 2011. – 352 с.

2. Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах: Учебное пособие. – М.: Высшая школа, 2002.- 544 с.

Временной ресурс:

- аудиторные занятия – 4 часа;

- самостоятельная работа – 16 часов.

Лабораторная работа № 1

Тема: Численные методы одномерной минимизации.

Цель работы: Приобретение практических навыков для решения задач одномерной минимизации численными методами.

Постановка задачи

Требуется найти безусловный минимум функции одной переменной , то есть, такую точку , что .

Поставленная задача может быть решена с помощью необходимых и достаточных условий безусловного экстремума. Однако, во многих практических случаях найти производные от заданной функции не представляется возможным. Поэтому решение задач одномерной оптимизации численными методами является актуальным при изучении методов оптимизации.

Численные методы одномерной минимизации

К основным численным методам одномерной минимизации относят:

- метод равномерного поиска;

- метод деления отрезка пополам;

- метод дихотомии;

- метод золотого сечения;

- метод Фибоначчи;

- метод квадратичной интерполяции и др.

Метод равномерного поиска

Метод относится к пассивным стратегиям поиска точки экстремума. Задается начальный интервал неопределенности 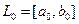и количество вычислений 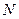. Вычисления производятся в 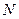равноотстоящих друг от друга точках. При этом интервал делится на 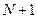равных интервалов. Путем сравнения величин находится точка , в которой значение функции наименьшее. Искомая точка считается заключенной в интервале .