Способы отбора, обеспечивающие репрезентативность выборки

Достоверность рассчитанных по выборочным данным характеристик в значительной степени определяется репрезентативностью выборочной совокупности, которая, в свою очередь, зависит от способа отбора единиц из генеральной совокупности. В каждом конкретном случае в зависимости от целого ряда условий, а именно, сущности исследуемого явления, объема совокупности, вариации и распределения наблюдаемых признаков, материальных и трудовых ресурсов, выбирают наиболее предпочтительную систему организации отбора, которая определяется видом, методом и способом отбора.

По виду различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности, при групповом отборе – группы единиц, а комбинированный отбор предполагает сочетание группового и индивидуального отбора.

Метод отбора определяет возможность продолжения участия отобранной единицы в процедуре отбора.

Бесповторным называется отбор, при котором попавшая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор.

При повторном отборе попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в исходную (генеральную) совокупность для участия в дальнейшей процедуре отбора. Повторный метод отбора применяется в тех случаях, когда характер исследуемого явления предполагает возможность повторной регистрации единиц. Такая возможность, прежде всего, может иметь место в выборочных обследованиях населения в качестве покупателей, пациентов, избирателей, абитуриентов и т.д.

Способ отбора определяет конкретный механизм или процедуру выборки единиц из генеральной совокупности.

Понятие о малой выборке

Малой выборкой называется такое выборочное наблюдение, численность единиц которого не превышает 30. Разработка теории малой выборки была начата английским статистиком В.С.Госсетом ( псевдоним Стьюдент). Он доказал, что оценка расхождений между средней малой выборки и генеральной средней имеет особый закон распределения.

При оценке результатов малой выборки величина генеральной совокупности не используется. Для определения возможных пределов ошибки используется критерий Стьюдента, определяемый по формуле:

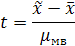
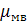- средняя ошибка малой выборки.

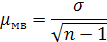
Величина 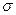вычисляется на основе данных выборочного наблюдения. Она равна:

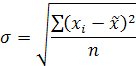Предельная ошибка малой выборки в зависимости от средней ошибки определяется следующим образом: .

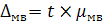Для малой выборки величина коэффициента доверия (критерия t) по-другому связана с вероятностной оценкой, чем при большой выборке, так как закон распределения отличается от нормального.

37.динамические ряды: понятие и их характеристика Выявление закономерностей развития и прогнозирования изменения будущей соц эк действий явл целью изуч любого общест явл. Исслед учитывающие измен факторов можно разбить на сл этапы: 1) анализ фактических данных 2) прогнозирование развития явления 3) сравнение прогнозных значений и фактических данных; корректировка аналитических выводов и закономерностей развития явления.

Включение фактора времени в систему аналитических показателей описывающих систему в статистике называется динамикой. Изменение явл отображается с помощью нескольких хронологически упорядоченных значений признака характеризующих это явление в различные временные промежутки. Такое отображение называется рядом динамики, а отдельные значения признака – уровнями ряда динамики. Ряд динамики имеет два осн характеристики по которым они классиф: 1) тип данных(ряд динамики абсолютных, относительных, средних величин) 2) период времени(моментный, интервальный).