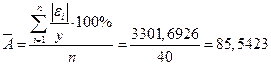Отображение на графике данных модели

Построение графиков осуществляется с помощью Мастера диаграмм. Последовательность действия действий представлена на рисунках 11–14.

Рисунок 11. Диалоговое окно Мастера диаграмм: тип диаграмм	Рисунок 12. Диалоговое окно Мастера диаграмм: исходные данные
Рисунок 13. Диалоговое окно Мастера диаграмм: параметры диаграммы	Рисунок 14. Диалоговое окно Мастера диаграмм: размещение диаграммы

Результатом выполнения Мастера диаграмм является диаграмма (см. рис. 15).

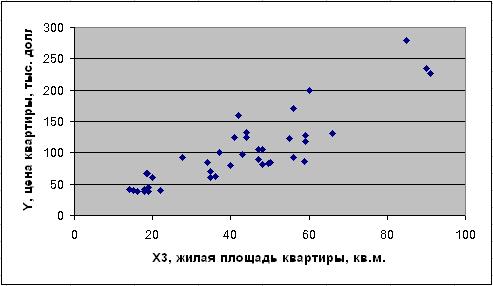
Рисунок 15. Поле корреляции (диаграмма рассеивания)

3 Расчет параметров линейной парной регрессии для всех факторов Х

3.1. Расчет параметров линейной парной регрессии для фактора Х1.

1 СПОСОБ.Расчет параметров линейной парной регрессии по формулам. Уравнение линейной регрессии от фактора Х1 имеет вид: 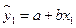. Для расчета всех параметров воспользуемся значениями таблицы 1.

Значения параметров a и b линейной модели определяются по формулам:

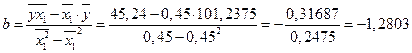
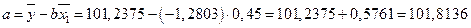
Уравнение регрессии имеет вид: .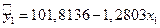

Таблица 1

Исходные и промежуточные значения для расчета адекватности модели

№
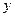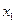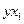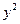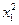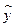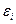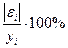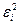						100,5333	-62,5333	164,5613	3910,4136
	62,2		62,2	3868,84		100,5333	-38,3333	61,6291	1469,4419
						-1,2803	126,2803	101,0242	15946,7142
	61,1		61,1	3733,21		100,5333	-39,4333	64,5390	1554,9851
						-1,2803	68,2803	101,9109	4662,1994
						-1,2803	94,2803	101,3767	8888,7750
						100,5333	17,4667	14,8023	305,0856
						-1,2803	133,2803	100,9699	17763,6384
	92,5			8556,25		-1,2803	93,7803	101,3841	8794,7447
						100,5333	4,4667	4,2540	19,9514
						100,5333	-58,5333	139,3650	3426,1472
						100,5333	24,4667	19,5734	598,6194
						-1,2803	171,2803	100,7531	29336,9412
						-1,2803	39,2803	103,3692	1542,9420
	130,5			17030,25		-1,2803	131,7803	100,9811	17366,0475
						-1,2803	86,2803	101,5062	7444,2902
						-1,2803	99,2803	101,3064	9856,5780
						-1,2803	129,2803	101,0002	16713,3960
						-1,2803	86,2803	101,5062	7444,2902
						100,5333	59,4667	37,1667	3536,2884
						-1,2803	61,2803	102,1338	3755,2752
						100,5333	-59,5333	145,2032	3544,2138
						100,5333	-10,5333	11,7037	110,9504
						-1,2803	84,2803	101,5425	7103,1690
						-1,2803	46,2803	102,8451	2141,8662
						-1,2803	40,2803	103,2828	1622,5026
	86,9			7551,61		-1,2803	88,1803	101,4733	7775,7653
						-1,2803	41,2803	103,2008	1704,0632
						-1,2803	81,2803	101,6004	6606,4872
						-1,2803	228,2803	100,5640	52111,8954
						-1,2803	236,2803	100,5448	55828,3802
						100,5333	-60,5333	151,3333	3664,2804
						100,5333	-33,5333	50,0497	1124,4822
						100,5333	22,4667	18,2656	504,7526
						-1,2803	101,2803	101,2803	10257,6992
						100,5333	4,4667	4,2540	19,9514
	70,3		70,3	4942,09		100,5333	-30,2333	43,0061	914,0524
						100,5333	-18,5333	22,6016	343,4832
						100,5333	179,4667	64,0953	32208,2964
						100,5333	99,4667	49,7334	9893,6244
Сумма	4049,5		1809,6	537970,25		1781,4328	2268,0672	3301,6926	361816,6796
Среднее значение	101,2375	0,45	45,24	13449,256	0,45	44,5358	56,7017	82,5423	9045,4170

2 способ. Расчет параметров линейной парной регрессии с помощью MS Excel. Уравнение линейной регрессии от фактора Х1 имеет вид: 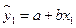. Воспользуемся инструментом анализа данных Регрессия (Сервис → Анализ данных). Вводим необходимые параметры (см. рис. 16).

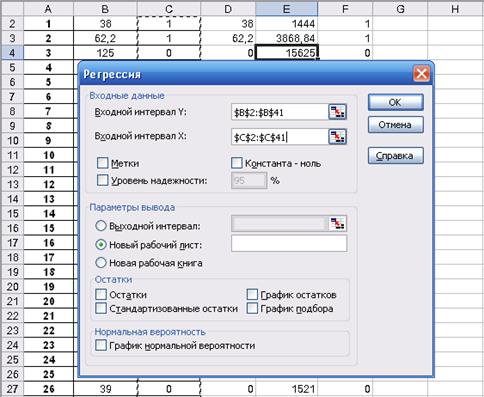
Рисунок 16. Диалоговое окно инструмента Регрессия

Результатом выполнения инструмента Регрессия является совокупность таблиц (см. рис. 17).

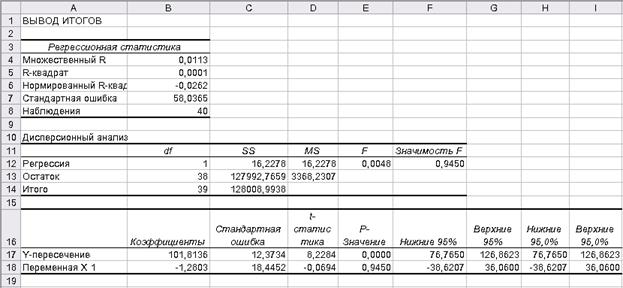
Рисунок 17. Результат выполнения инструмента Регрессия

В ячейках В17 и В18 отражены значения коэффициентов линейной регрессии a и b соответственно. Следовательно, уравнение линейной регрессии имеет вид:

.

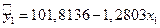3.2. Расчет параметров линейной парной регрессии для фактора Х2.

1 СПОСОБ.Расчет параметров линейной парной регрессии по формулам. Уравнение линейной регрессии от фактора Х2 имеет вид: 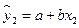. Для расчета всех параметров воспользуемся значениями таблицы 2.

Таблица 2

№
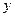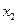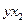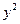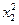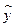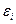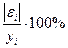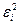						43,5771	-5,5771	14,6766	31,1040
	62,2		124,4	3868,84		79,6149	-17,4149	27,9982	303,2787
						115,6527	9,3473	7,4778	87,3720
	61,1		122,2	3733,21		79,6149	-18,5149	30,3026	342,8015
						43,5771	23,4229	34,9596	548,6322
						79,6149	13,3851	14,3926	179,1609
						115,6527	2,3473	1,9892	5,5098
						115,6527	16,3473	12,3843	267,2342
	92,5		277,5	8556,25		115,6527	-23,1527	25,0299	536,0475
						151,6905	-46,6905	44,4671	2180,0028
						43,5771	-1,5771	3,7550	2,4872
						115,6527	9,3473	7,4778	87,3720
						151,6905	18,3095	10,7703	335,2378
						43,5771	-5,5771	14,6766	31,1040
	130,5			17030,25		151,6905	-21,1905	16,2379	449,0373
						79,6149	5,3851	6,3354	28,9993
						151,6905	-53,6905	54,7862	2882,6698
						151,6905	-23,6905	18,5082	561,2398
						115,6527	-30,6527	36,0620	939,5880
						115,6527	44,3473	27,7171	1966,6830
						43,5771	16,4229	27,3715	269,7116
						43,5771	-2,5771	6,2856	6,6414
						151,6905	-61,6905	68,5450	3805,7178
						151,6905	-68,6905	82,7596	4718,3848
						43,5771	1,4229	3,1620	2,0246
						43,5771	-4,5771	11,7362	20,9498
	86,9		260,7	7551,61		115,6527	-28,7527	33,0871	826,7178
						43,5771	-3,5771	8,9427	12,7956
						79,6149	0,3851	0,4814	0,1483
						151,6905	75,3095	33,1760	5671,5208
						151,6905	83,3095	35,4509	6940,4728
						43,5771	-3,5771	8,9427	12,7956
						43,5771	23,4229	34,9596	548,6322
						151,6905	-28,6905	23,3256	823,1448
						115,6527	-15,6527	15,6527	245,0070
						115,6527	-10,6527	10,1454	113,4800
	70,3		140,6	4942,09		79,6149	-9,3149	13,2502	86,7674
						115,6527	-33,6527	41,0399	1132,5042
						151,6905	128,3095	45,8248	16463,328
						151,6905	48,3095	24,1548	2333,8078
Сумма	4049,5		12532,4	537970,25		4049,5032	-0,00320	938,2983	55800,1144
Среднее значение	101,2375	2,6	313,31	13449,2563	8,15	101,2376	-0,00008	23,4575	1395,00286

Значения параметров a и b линейной модели определяются по формулам:

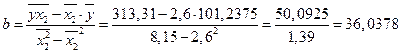
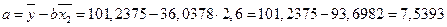
Уравнение регрессии имеет вид: .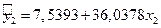

2 СПОСОБ. Расчет параметров линейной парной регрессии с помощью MS Excel. Уравнение линейной регрессии от фактора Х2 имеет вид: 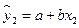. Воспользуемся инструментом анализа данных Регрессия (Сервис → Анализ данных). Вводим необходимые параметры (см. рис. 18).

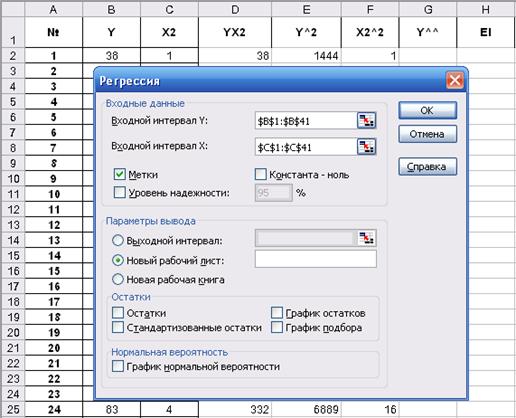
Рисунок 18.Диалоговое окно инструмента Регрессия

Результатом выполнения инструмента Регрессия является совокупность таблиц (см. рис. 19).

В ячейках В17 и В18 отражены значения коэффициентов линейной регрессии a и b соответственно. Следовательно, уравнение линейной регрессии имеет вид:

.

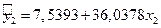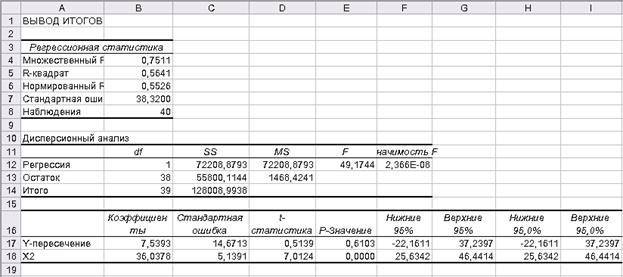
Рисунок 19. Результат выполнения инструмента Регрессия

3.3. Расчет параметров линейной парной регрессии для фактора Х3.

1 СПОСОБ.Расчет параметров линейной парной регрессии по формулам. Уравнение линейной регрессии от фактора Х3 имеет вид: 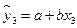. Для расчета всех параметров воспользуемся значениями таблицы 3.

Таблица 3

№
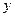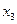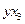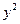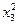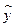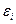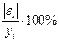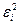						44,1791	-6,1791	16,2608	38,1813
	62,2		2239,2	3868,84		86,2711	-24,0711	38,6995	579,4179
						98,6511	26,3489	21,0791	694,2645
	61,1	34,8	2126,28	3733,21	1211,04	83,2999	-22,1999	36,3337	492,8356
		18,7	1252,9		349,69	43,4363	23,5637	35,1697	555,2480
		27,7	2576,1		767,29	65,7203	27,2797	29,3330	744,1820
						143,2191	-25,2191	21,3721	636,0030
						106,0791	25,9209	19,6370	671,8931
	92,5			8556,25		135,7911	-43,2911	46,8012	1874,1193
						113,5071	-8,5071	8,1020	72,3708
						41,7031	0,2969	0,7069	0,0881
						106,0791	18,9209	15,1367	358,0005
						135,7911	34,2089	20,1229	1170,2488
						36,7511	1,2489	3,2866	1,5598
	130,5			17030,25		160,5511	-30,0511	23,0277	903,0686
						81,3191	3,6809	4,3305	13,5490
						103,6031	-5,6031	5,7174	31,3947
		59,2	7577,6		3504,64	143,7143	-15,7143	12,2768	246,9392
						120,9351	-35,9351	42,2766	1291,3314
						101,1271	58,8729	36,7956	3466,0184
						46,6551	13,3449	22,2415	178,0864
						31,7991	9,2009	22,4412	84,6566
						113,5071	-23,5071	26,1190	552,5838
		49,5	4108,5		2450,25	119,6971	-36,6971	44,2134	1346,6771
		18,9	850,5		357,21	43,9315	1,0685	2,3744	1,1417
						41,7031	-2,7031	6,9310	7,3067
	86,9	58,7	5101,03	7551,61	3445,69	142,4763	-55,5763	63,9543	3088,7251
						51,6071	-11,6071	29,0178	134,7248
						96,1751	-16,1751	20,2189	261,6339
						222,4511	4,5489	2,0039	20,6925
						219,9751	15,0249	6,3936	225,7476
						34,2751	5,7249	14,3123	32,7745
		18,5	1239,5		342,25	42,9411	24,0589	35,9088	578,8307
						133,3151	-10,3151	8,3863	106,4013
						88,7471	11,2529	11,2529	126,6278
						115,9831	-10,9831	10,4601	120,6285
	70,3	34,8	2446,44	4942,09	1211,04	83,2999	-12,9999	18,4920	168,9974
						115,9831	-33,9831	41,4428	1154,8511
						207,5951	72,4049	25,8589	5242,4695
						145,6951	54,3049	27,1525	2949,0222
Сумма	4049,5	1681,8	209755,05	537970,25	86662,1	4049,5408	-0,0408	875,6413	30223,2929
Среднее значение	101,2375	42,045	5243,8763	13449,2563	2166,5525	101,2385	-0,0010	21,8910	755,5823

Значения параметров a и b линейной модели определяются по формулам:

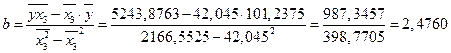
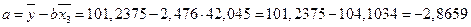
Уравнение регрессии имеет вид: .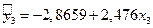

2 СПОСОБ. Расчет параметров линейной парной регрессии с помощью MS Excel. Уравнение линейной регрессии от фактора Х2 имеет вид: 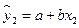. Воспользуемся инструментом анализа данных Регрессия (Сервис → Анализ данных). Вводим необходимые параметры (см. рис. 20).

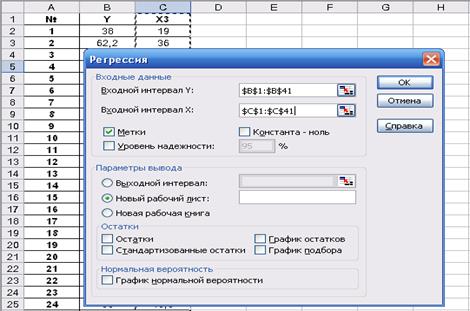
Рисунок 20.Диалоговое окно инструмента Регрессия

Результатом выполнения инструмента Регрессия является совокупность таблиц (см. рис. 21).

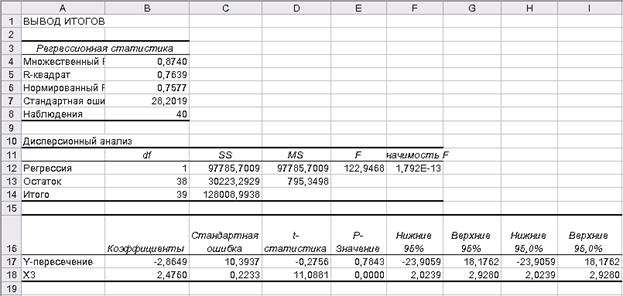
Рисунок 21.Результат выполнения инструмента Регрессия

В ячейках В17 и В18 отражены значения коэффициентов линейной регрессии a и b соответственно. Следовательно, уравнение линейной регрессии имеет вид:

.

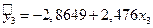Оценка качества моделей

4.1 Оценка качества линейной парной регрессии для фактора Х1

Для оценки качества модели используются коэффициент детерминации, средняя ошибка аппроксимации и F-критерий Фишера.

1 СПОСОБ. Использование формул.

Определим линейный коэффициент парной корреляции по следующей формуле:

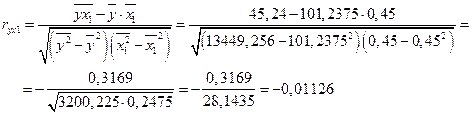
Можно сказать, что связь между ценой квартиры Y и городом области X1 достаточно мала (1,13%). Определим коэффициент детерминации по формуле:

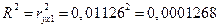
Вариация результата Y (цены офиса) на 0,01% объясняется вариацией фактора Х1 (города области).

Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера. Определим F-критерий Фишера по формуле:

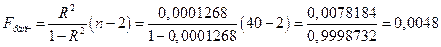
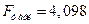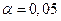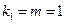при , и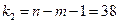

Так как 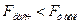, то уравнение регрессии с доверительной вероятностью 0,95% является статистически незначимым.

Средняя относительная ошибка определяется по формуле: