Тема 3. ЛИНЕЙНАЯ МНОЖЕСТВЕННАЯ

СОДЕРЖАНИЕ

Введение………………………………………….. 4

Тема 1. ЛИНЕЙНАЯ ПАРНАЯ РЕГРЕССИЯ…. 6

Лабораторная работа № 1.1 ………………………… 6

Лабораторная работа № 1.2 ………………………… 7

Лабораторная работа № 1.3 ………………………… 9

Лабораторная работа № 1.4 ………………………… 11

Лабораторная работа № 1.5 ………………………… 13

Лабораторная работа № 1.6 ………………………… 15

Тема 2. НЕЛИНЕЙНАЯ ПАРНАЯ РЕГРЕССИЯ... 17

Лабораторная работа № 2.1 ………………….……… 17

Лабораторная работа № 2.2 ………………………… 22

Тема 3. ЛИНЕЙНАЯ МНОЖЕСТВЕННАЯ

РЕГРЕССИЯ………………………………. 24

Лабораторная работа № 3.1 ………………………… 25

Лабораторная работа № 3.2 ………………………… 28

Тема 4. НЕЛИНЕЙНАЯ МНОЖЕСТВЕННАЯ

РЕГРЕССИЯ………………………………. 35

Лабораторная работа № 4.1 ………………………… 35

КОНТРОЛЬНАЯ РАБОТА № 1…………………. 39

КОНТРОЛЬНАЯ РАБОТА № 2 …………………. 41

ЛИТЕРАТУРА ……………………………………… 43

Введение

Построение эконометрических моделей обуславливает (особенно при большом объеме исходных данных) существенный объем вычислений и требует использование вычислительной техники и соответствующего программного обеспечения. Удобной универсальной вычислительной средой для решения задач эконометрики является табличный процессор Excel. При использовании Excel многие студенты сталкиваются с существенными трудностями реализации расчетных соотношений в Excel. Это вызвано тем, что этой стороне изучения эконометрики в учебной литературе уделяется крайне мало внимания, что затрудняет использования современных алгоритмов решения эконометрических задач на практике.

Поэтому основной целью данных методических указаний является изложение (в форме лабораторных работ) численных методик решения основных задач парного и множественного регрессионного анализа в вычислительной среде табличного процессора Excel.

Каждая лабораторная работа посвящена решению определенной задачи (или подзадачи) эконометрики (например, вычисление коэффициентов линейного уравнения регрессии). Для каждой лабораторной работы приводится алгоритм решения рассматриваемой в работе задачи (т.е. формулы или расчетные соотношения), а затем дается фрагмент документа Excel , реализующий алгоритм решения задачи.

При этом алгоритм решения может быть реализован путем программирования арифметических или логических выражений в ячейках электронной таблицы или путем обращения к «стандартным» функциям или модулям Excel. Поэтому предполагается, что читатель знаком с адресацией ячеек (относительной, абсолютной и смешанной), арифметическими операциями и программированием простейших выражений в ячейках Excel.

Хотя методические указания и содержат необходимые расчетные соотношения, но они не заменяет учебник по эконометрике, а является своеобразным справочником по численному решению некоторых задач эконометрике в Excel.

Замечание 1. В тексте при описании той или иной функции в качестве формальных параметров используются имена переменных, определенные в тексте пособия. При обращении к функции в качестве фактических параметров могут использоваться константы, адреса ячеек, диапазоны адресов и арифметические выражения. Например, описание функции для вычисления среднего арифметического значения (выборочного среднего) имеет вид:

СРЗНАЧ( ,

где – формальные параметры, число которых не превышает 30 ( ). Для вычисления среднего значения величин, находящихся в ячейках B3, B4, B5, B6, C3, C4, C5, C6, обращение к функции в соответствующей ячейке имеет вид

= СРЗНАЧ(B3:B6;С3:C6),

т.е. в качестве фактических параметров используются два диапазона ячеек.

Замечание 2. Так как в запрограммированной ячейке выводится результат вычислений и не видно самого запрограммированного выражения, то в некоторых случаях рядом с результатом приводится (в другой ячейке) запрограммированное выражение (своеобразный комментарий к выполняемым вычислениям). В случаях, когда не очевидно к какой ячейке относится приводимое выражение, используется стрелка, указывающая на нужную ячейку.

Методические указания включают также описание двух контрольных работ по построению парной и множественной регрессии. Выполнив лабораторные работы, студент может по аналогии выполнить 90 % вычислений, требуемых лабораторными работами. Заметим, что приведенные лабораторные работы позволят не только успешно выполнить контрольные работы, но и использовать методы эконометрики при решении практических задач регрессионного анализа экономических и социальных процессов.

Лабораторная работа № 1.1

Лабораторная работа № 1.2

Лабораторная работа № 1.3

Лабораторная работа № 1.4

Лабораторная работа № 1.5

Лабораторная работа № 1.6

По критерию Фишера

Цель работы. По данным таблицы 1.1 оценить на уровне a = 0.05 значимость уравнения регрессии 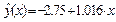, построенного в лабораторной работе № 1.1.

Расчетные соотношения. Уравнение парной регрессии значимо с уровнем значимости a, если выполняется следующее неравенство:

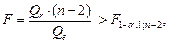(1.14)

где F_{g; 1; n-2} – значения квантиля уровня g F-распределения с числами степеней свободы k₁ = 1 и k₂ = n – 2. Для вычисления квантиля можно использовать следующее выражение

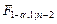= FРАСПОБР( 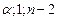). (1.15)

Суммы 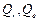, входящие в (1.14) определяются выражениями:

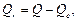
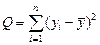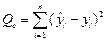, . (1.16)

Критерий (1.14) часто называют критерием Фишера или F-критерием.

Решение. На рис. 1.6 приведен фрагмент документа Excel, вычисляющего значения Q_e , 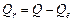и критерий F. В столбце D значения вычисляются по формуле 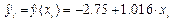. Значения коэффициентов 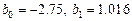взяты из лабораторной работы № 1.1.

Получены следующие значения 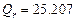, , 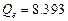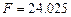. По формуле (1.15) вычисляем квантиль F_{0.95; 1; 8} = 5.32. Неравенство (1.14) выполняется, т. е. 24.04 > 5.32 и поэтому уравнение регрессии 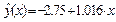значимо с уровнем значимости a = 0.05.

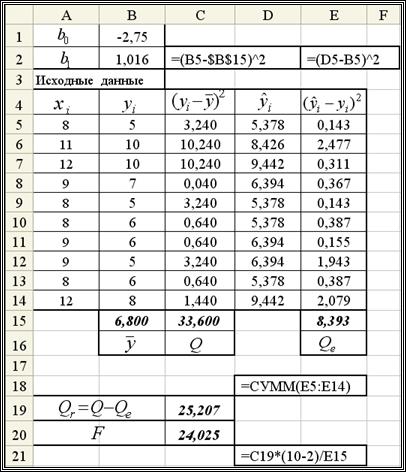
Рис. 1.6. Вычисление величины F – критерия

Лабораторная работа № 2.1

Команды

«Добавить линию тренда»

Цель работы. Используя пространственную выборку таблицы 2.1 необходимо построить уравнение нелинейной регрессии вида 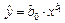с использованием команды «Добавить линию тренда» и вычислить коэффициент детерминации .

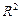Команда «Добавить линию тренда». Используется для выделения тренда (медленных изменений) при анализе временных рядов. Однако эту команду можно использовать и для построения уравнения нелинейной регрессии, рассматривая в качестве времени 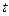независимую переменную .

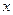Эта команда позволяет построить следующие уравнения регрессии:

· линейную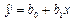

· полиноминальную ( );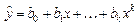

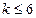· логарифмическую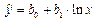

· степенную ;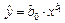

· экспоненциальную .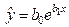

Для построения одной из перечисленных регрессий необходимо выполнить следующие шаги:

Шаг 1. В выбранном листе Excel ввести по столбцам исходные данные 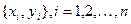(см. рис. 2.1).

Шаг 2. По этим данным построить график в декартовый системе координат (см. рис 2.1).

Шаг 3. Установить курсор на построенном графике, сделать щелчок правой кнопкой и в появившемся контекстном меню выполнить команду Добавить линию тренда (см. рис. 2.1).

Шаг 4. В появившемся диалоговом окне (см. рис. 2.2) активизировать закладку «Тип» и выбрать нужное уравнение регрессии.

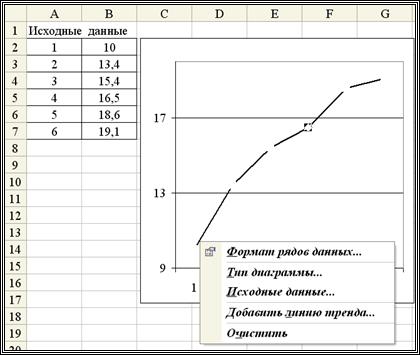
Рис. 2.1. Построение графика по исходным данным

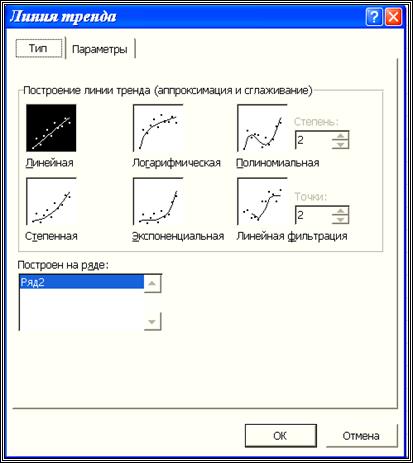
Рис. 2.2. Выбор вида уравнения регрессии

Шаг 5. Активизировать закладку «Параметры» (см. рис. 2.3) и «включить» необходимые для нас опции:

· «Показать уравнение на диаграмме» - на диаграмме будет показано выбранное уравнение регрессии с вычисленным коэффициентами;

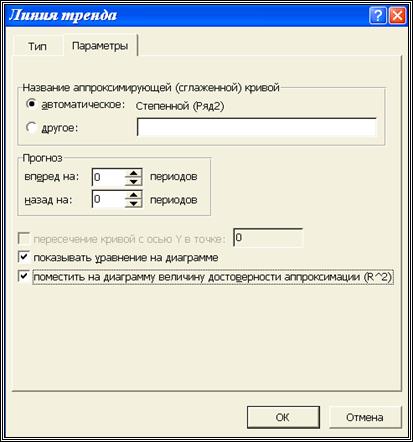
Рис. 2.3. Задание опций вывода информации

· «Поместить на диаграмму величину достоверности аппроксимации (R^2)» - на диаграмме будет показана значение коэффициент детерминации 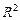(для нелинейной регрессии -индекс детерминации), вычисляемый по формул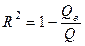е , где 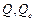определяются (1.16). Если по построенному уравнению регрессии необходимо выполнить прогноз, то нужно указать число периодов прогноза (см. рис. 2.3).

Назначение других опций понятны из своих названий.

Шаг 6. После задания всех перечисленных опций щелкнуть на кнопке «OK» и на диаграмме появиться формула построенного уравнения регрессии и значение индекса детерминации 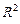(выделено на рис. 2.4 затемнением).

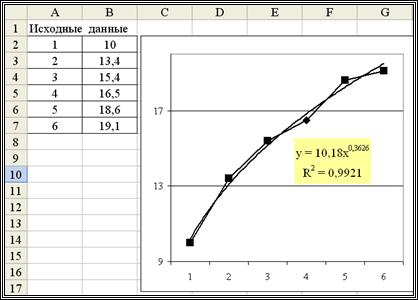
Рис. 2.4. График и уравнение построенной регрессии

Решение. Построение уравнения 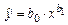осуществляем по описанным выше шагам. Получаем уравнение

,

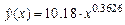для которого коэффициент детерминации равен (см. рис. 2.4). Такая величина говорит о хорошем соответствии построенного уравнения исходным данным.

Лабораторная работа № 2.2

Лабораторная работа № 3.1

Лабораторная работа № 3.2

Вычисление коэффициентов линейной множественной регрессии и проверка значимости в режиме Регрессия

Цель работы. Используя пространственную выборку таблицы 3.1 и используя режим Регрессия необходимо вычислить вектор коэффициентов уравнения регрессии

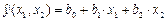. (3.4)

Режим Регрессия модуля Анализ данных. Табличный процессор Excel содержит модуль Анализ данных. Этотмодуль позволяет выполнить статистический анализ выборочных данных (построение гистограмм, вычисление числовых характеристик и т.д.). Режим работы Регрессия этого модуля осуществляет вычисление коэффициентов линейной множественной регрессии с 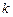переменными, построение доверительные интервалы и проверку значимости уравнения регрессии.

Для вызова режима Регрессиямодуля Анализ данных необходимо:

· обратиться к пункту менюСервис;

· в появившемся меню выполнить команду Анализ данных;

· в списке режимов работы модуля Анализ данных выбрать режим Регрессия и щелкнуть на кнопке Ok.

После вызова режимаРегрессияна экране появляется диалоговое окно (см. рис. 3.2), в котором задаются следующие параметры:

1. Входной интервал Y – вводится диапазон адресов ячеек, содержащих значения 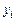(ячейки должны составлять один столбец).

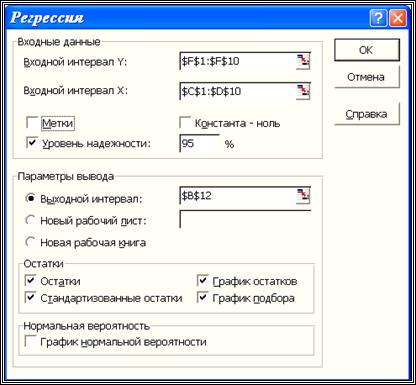
Рис. 3.2. Диалоговое окно режима Регрессия

2. Входной интервал X – вводится диапазон адресов ячеек, содержащих значения независимых переменных. Значения каждой переменной представляются одним столбцом. Количество переменных не более 16 (т.е. ).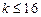

3. Метки – включается если первая строка во входном диапазоне содержит заголовок. В этом случае автоматически будут созданы стандартные названия.

4. Уровень надежности – при включении этого параметра задается надежность 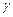при построении доверительных интервалов.

5. Константа-ноль – при включении этого параметра коэффициент .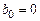

6. Выходной интервал – при включении активизируется поле, в которое необходимо ввести адрес левой верхней ячейки выходного диапазона, который содержит ячейки с результатами вычислений режима Регрессия.

7. Новый рабочий лист – при включении этого параметра открывается новый лист, в который начиная с ячейки А1 вставляются результаты работы режима Регрессия.

8. Новая рабочая книга - при включении этого параметра открывается новая книга на первом листе которой начиная с ячейки А1 вставляются результаты работы режима Регрессия.

9. Остатки – привключении вычисляется столбец, содержащий невязки .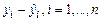

10. Стандартизованные остатки – при включении вычисляется столбец, содержащий стандартизованные остатки.

11. График остатков – при включении выводятся точечные графики невязки 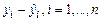, в зависимости от значений переменных 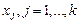. Количество графиков равно числу 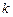переменных .

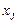12. График подбора – при включении выводятся точечные графики предсказанных по построенной регрессии значений 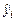от значений переменных 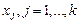. Количество графиков равно числу 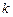переменных .

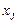Решение. Первоначально введем в столбец С десять значений первой переменной, в столбец D - десять значений первой переменной (см. рис. 3.2), а в столбец F – десять значений зависимой переменной.

После этого вызовем режим Регрессия и в диалоговом окне зададим необходимые параметры (см. рис. 3.2). Результаты работы приводятся рис. 3.3 – 3.5. Заметим, из-за большой «ширины» таблиц, в которых выводятся результаты работы режима Регрессия, часть результатов помещены в другие ячейки.

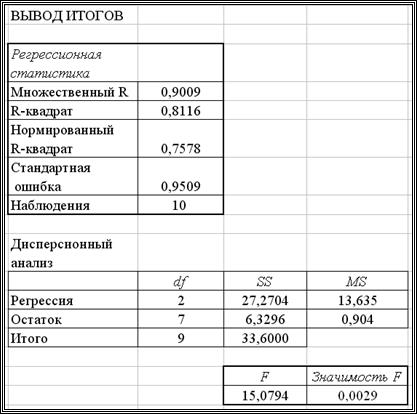
Рис. 3.3. Результаты работы режима Регрессия

Дадим краткую интерпретацию показателям, значения которых вычисляются в режиме Регрессия. Первоначально рассмотрим показатели, объединенные названием Регрессионная статистика (см. рис. 3.3).

Множественный 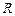- корень квадратный из коэффициента детерминации.

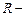квадрат – коэффициент детерминации .

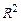Нормированный 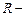квадрат – приведенный коэффициент детерминации 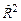(см. формулу (2.1)).

Стандартная ошибка – оценка 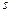для среднеквадратического отклонения .

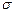Наблюдения – число наблюдений .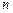

Перейдем к показателям, объединенных названием Дисперсионный анализ (см. рис. 3.3).

Столбец 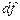- число степеней свободы. Для строки Регрессия показатель равен числу независимых переменных 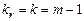; для строки Остаток - равен 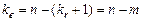; для строки Итого – равен .

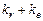Столбец SS – сумма квадратов отклонений. Для строки Регрессия показатель равен величине 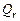(см. формулы (1.16)), т.е.

;

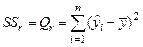для строки Остаток - равен величине 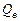(см. формулы (1.16)), т.е.

;

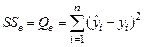для строки Итого – равен .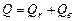

Столбец 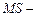дисперсии, вычисленные по формуле

,

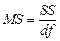т.е. дисперсия на одну степень свободы.

Столбец 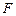– значение 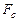, равное 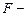критерию Фишера, вычисленного по формуле:

.

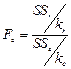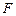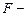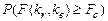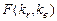Столбец значимость - значение уровня значимости, соответствующее вычисленной величине критерия и равное вероятности , где - случайная величина, подчиняющаяся распределению Фишера с 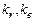степенями свободы. Эту вероятность можно также определить с помощью функции FРАСП( 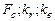). Если вероятность меньше уровня значимости 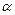(обычно 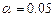), то построенная регрессия является значимой..

Перейдем к следующей группе показателей, объединенных в таблице, показанной на рис. 3.4.

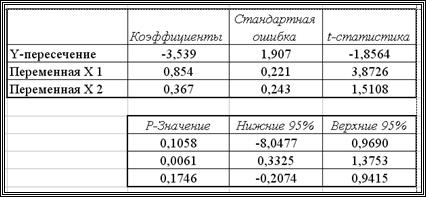
Рис. 3.4. Продолжение результатов работы режима Регрессия

Столбец Коэффициенты – вычисленные значения коэффициентов 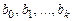, расположенных сверху-вниз.

Столбец Стандартная ошибка – значения 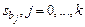, вычисленные по формуле .

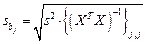Столбец 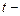статистика – значения статистик .

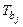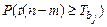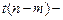Столбец Р – значение – содержит вероятности случайных событий , где случайная величина, подчиняющаяся распределению Стьюдента с 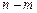степенями свободы.

Если эта вероятность меньше уровня значимости 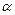, то принимается гипотеза о значимости соответствующего коэффициента регрессии.

Из рис. 3.4 видно, что значимым коэффициентом является только коэффициент .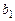

Столбцы Нижние 95% и Верхние 95% - соответственно нижние и верхние интервалы для оцениваемых коэффициентов .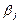

Перейдем к следующей группе показателей, объединенных в таблице, показанной на рис. 3.5.

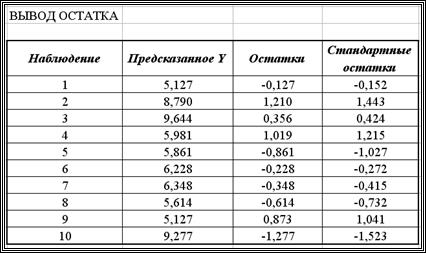
Рис. 3.5. Продолжение результатов работы режима Регрессия

Столбец Наблюдение – содержит номера наблюдений.

Столбец Предсказанное У – значения 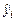, вычисленные по построенному уравнению регрессии.

Столбец Остатки – значения невязок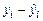

В заключении рассмотрения результатов работы режима Регрессия приведем график невязок (на рисунке 3.6 невязки названы остатками) при заданных значениях только второй переменной. Наличие чередующихся положительных и отрицательных значений невязок является косвенным признаком отсутствия систематической ошибки (неучтенной независимой переменной) в построенном уравнении регрессии.

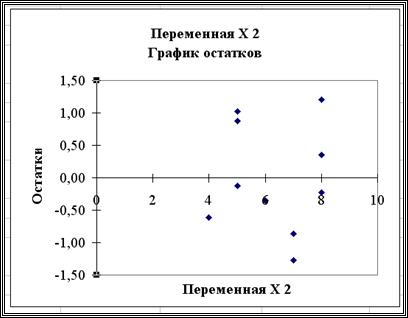
Рис. 3.6. График невязок как функция переменной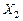

Лабораторная работа № 4.1.

Контрольная работа № 1

Парная регрессия

Данные, характеризующие прибыль торговой компании «Все для себя» за первые 10 месяцев 2005 года (в тыс. руб.), даны в следующей таблице:

Таблица К1

январь	февраль	март	апрель	май
382 + N	402 + N	432+ N	396+ N	454+ N
июнь	июль	август	сентябрь	октябрь
419+ N	460+ N	447+ N	464+ N	498+ N

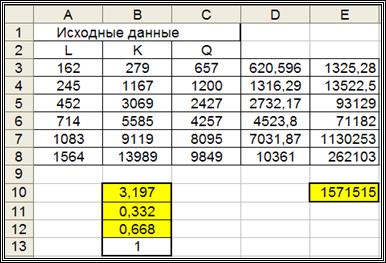
Рис. 3.9. Результаты работы команды Поиск решения

В этой таблице 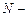две последних цифры номера зачетной книжки студента.

Требуется:

1. Построить диаграмму рассеяния.

2. Убедится в наличии тенденции (тренда) в заданных значениях прибыли фирмы и возможности принятия гипотезы о линейном тренде.

3. Построить линейную парную регрессию (регрессию вида 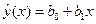). Вычисление коэффициентов 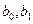выполнить методом наименьших квадратов.

4. Нанести график регрессии на диаграмму рассеяния.

5. Вычислить значения статистики 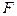и коэффициента детерминации 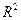. Проверить гипотезу о значимости линейной регрессии.

6. Вычислить выборочный коэффициент корреляции и проверить гипотезу о ненулевом его значении.

7. Вычислить оценку дисперсии случайной составляющей эконометрической модели.

8. Проверить гипотезы о ненулевых значениях коэффициентов .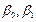

9. Построить доверительные интервалы для коэффициентов .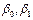

10. Построить доверительные интервалы для дисперсии случайной составляющей эконометрической модели.

11. Построить доверительную область для условного математического ожидания 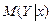(диапазон по оси январь – декабрь). Нанести границы этой области на диаграмму рассеяния.

12. С помощью линейной парной регрессии сделать прогноз величины прибыли и нанести эти значения на диаграмму рассеяния. Сопоставить эти значения с границами доверительной области для условного математического ожидания 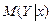и сделать вывод о точности прогнозирования с помощью построенной регрессионной модели.

Контрольная работа № 2

Библиографический список

1. Кремер Н. Ш.Эконометрика / Н. Ш. Кремер, Б. А. Путко. – М.: ЮНИТИ, 2002.

2. Айвазян С. А.Прикладная статистика и основы эконометрики / Айвазян С. А., В. С. Мхитарян. – М.: ЮНИТИ, 1998.

3. Эконометрика :под ред. Н. И. Елисеевой. – М. : Финансы и статистика, 2001.

4. Арженовский С. В. Эконометрика : учебное пособие /С. В. Арженовский, О. Н. Федосова. – Ростов н/Д, 2002.

5. Тихомиров Н. П.Эконометрика / Н. П. Тихомиров, Е. Ю. До­рохина. – М. : Экзамен, 2003.

СОДЕРЖАНИЕ

Введение………………………………………….. 4

Тема 1. ЛИНЕЙНАЯ ПАРНАЯ РЕГРЕССИЯ…. 6

Лабораторная работа № 1.1 ………………………… 6

Лабораторная работа № 1.2 ………………………… 7

Лабораторная работа № 1.3 ………………………… 9

Лабораторная работа № 1.4 ………………………… 11

Лабораторная работа № 1.5 ………………………… 13

Лабораторная работа № 1.6 ………………………… 15

Тема 2. НЕЛИНЕЙНАЯ ПАРНАЯ РЕГРЕССИЯ... 17

Лабораторная работа № 2.1 ………………….……… 17

Лабораторная работа № 2.2 ………………………… 22

Тема 3. ЛИНЕЙНАЯ МНОЖЕСТВЕННАЯ

РЕГРЕССИЯ………………………………. 24

Лабораторная работа № 3.1 ………………………… 25

Лабораторная работа № 3.2 ………………………… 28