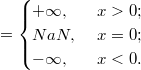Диапазон значений чисел с плавающей точкой
Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. Пара значений показателя (когда все разряды нули и когда все разряды единицы) зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся ноль, значения NaN (Not a Number, "не число", получается как результат операций типа деления нуля на ноль) и 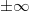 .
.
Данная таблица только лишь примерно указывает границы допустимых значений, без учета возрастающей погрешности с ростом абсолютного значения и существования денормализованных чисел.
| Название (IEEE 754) | Тип в языке программирования Cи | Диапазон | Биты мантиссы | Биты |
| Half precision | Нет | 6,10×10-5..65504 | 10+1 | |
| Single precision | float | 3,4×10-38..3,4×1038 | 23+1 | |
| Double precision | double | 1,7×10-308..1,7×10308 | 52+1 | |
| Extended precision | Нет, на некоторых архитектурах long double | 3,4×10-4932..3,4×104932 | 64+1 |
Машинная эпсилон (машинный ноль)
| Определение: | ||
Машинная эпсилон - наибольшее положительное число 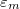 , такое что, , такое что, 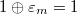 , где , где 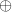 - машинное сложение. - машинное сложение. | ||
| Утверждение: | ||
Таким образом, компьютер не различает числа  и и 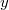 , если , если 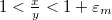 . . | ||
| Утверждение: | ||
Из свойств чисел двойной точности следует, что для них 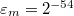 . . | ||
Особые значения чисел с плавающей точкой
Ноль (со знаком)
Как уже было оговорено выше, в нормализованной форме числа с плавающей точкой невозможно представить ноль. Поэтому для его представления зарезервированы специальные значения мантиссы и порядка - число считается нулём, если все его биты, кроме знакового, равны нулю. При этом в зависимости от значения бита знака ноль может быть как положительным, так и отрицательным.
Арифметика нуля со знаком
Арифметика отрицательного нуля аналогична таковой для любого отрицательного числа и понятна интуитивно. Вот несколько примеров:
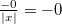 (если
(если 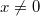 )
)
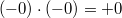
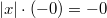
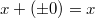
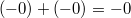
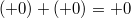
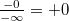
Неопределенность (NaN)
NaN - это аббревиатура от фразы "not a number". NaN является результатом арифметических операций, если во время их выполнения произошла ошибка (примеры см. ниже). В IEEE 754 NaN представлен как число, в котором все двоичные разряды порядка - единицы, а мантисса не нулевая.
| Знак | |||||||||||||||||
| Порядок | Мантисса | ||||||||||||||||
| 0/1 | 1, | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | = 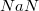 | |||||
Любая операция с NaN возвращает NaN. При желании в мантиссу можно записывать информацию, которую программа сможет интерпретировать. Стандартом это не оговорено и мантисса чаще всего игнорируется.
Как можно получить NaN?
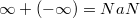
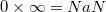
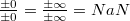
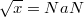 , где
, где 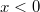
Есть и другие способы получения NaN, подробности можно найти по ссылкам в соответствующем разделе.
По определению NaN ≠ NaN, поэтому, для проверки значения переменной нужно просто сравнить ее с собой.
Бесконечности
В число с плавающей запятой можно записать значение 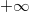 или
или 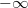 . Как и нули со знаком, бесконечности позволяют получить хотя бы близкий к правильному результат вычисления в случае переполнения. Согласно стандарту IEEE 754 число с плавающей запятой считается равным бесконечности, если все двоичные разряды его порядка - единицы, а мантисса равна нулю. Знак бесконечности определяется знаковым битом числа.
. Как и нули со знаком, бесконечности позволяют получить хотя бы близкий к правильному результат вычисления в случае переполнения. Согласно стандарту IEEE 754 число с плавающей запятой считается равным бесконечности, если все двоичные разряды его порядка - единицы, а мантисса равна нулю. Знак бесконечности определяется знаковым битом числа.
| Знак | |||||||||||||||||
| Порядок | Мантисса | ||||||||||||||||
| 0/1 | 1, | = 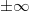 | |||||||||||||||
Получить бесконечность можно при переполнении и при делении ненулевого числа на ноль.