Диапазон значений чисел с плавающей запятой
Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. Пара значений показателя (когда все разряды нули и когда все разряды единицы) зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся ноль, значения NaN (Not a Number, "не число", получается как результат операций типа деления нуля на ноль) и 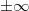 .
.
Данная таблица только лишь примерно указывает границы допустимых значений, без учета возрастающей погрешности с ростом абсолютного значения и существования денормализованных чисел.
| Название (IEEE 754) | Тип в языке программирования C | Диапазон | Биты мантиссы | Биты |
| Half precision | Нет | 6,10×10-5..65504 | 10+1 | |
| Single precision | float | 3,4×10-38..3,4×1038 | 23+1 | |
| Double precision | double | 1,7×10-308..1,7×10308 | 52+1 | |
| Extended precision | Нет, на некоторых архитектурах long double | 3,4×10-4932..3,4×104932 | 64+1 |
Особые значения чисел с плавающей точкой
Ноль (со знаком)
Как уже было оговорено выше, в нормализованной форме числа с плавающей точкой невозможно представить ноль. Поэтому для его представления зарезервированы специальные значения мантиссы и порядка - число считается нулём, если все его биты, кроме знакового, равны нулю. При этом в зависимости от значения бита знака ноль может быть быть как положительным, так и отрицательным.
| Знак | |||||||||||||||||
| Порядок | Мантисса | ||||||||||||||||
| 0/1 | 1, | = 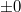 | |||||||||||||||
Арифметика нуля со знаком
Арифметика отрицательного нуля аналогична таковой для любого отрицательного числа и понятна интуитивно. Вот несколько примеров:
§ 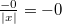 (если
(если 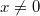 )
)
§ 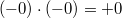
§ 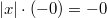
§ 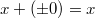
§ 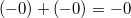
§ 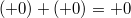
§ 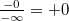
§ 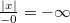 (если
(если 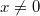 )
)
Неопределенность (NaN)
NaN - это аббревиатура от фразы "not a number". NaN является результатом арифметических операций, если во время их выполнения произошла ошибка (примеры см. ниже). В IEEE 754 NaN представлен как число, в котором все двоичные разряды порядка - единицы, а мантисса не нулевая.
| Знак | |||||||||||||||||
| Порядок | Мантисса | ||||||||||||||||
| 0/1 | 1, | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | = 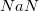 | |||||
Любая операция с NaN возвращает NaN. При желании в мантиссу можно записывать информацию, которую программа сможет интерпретировать. Стандартом это не оговорено и мантисса чаще всего игнорируется.
Как можно получить NaN?
§ 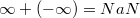
§ 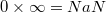
§ 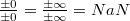
§ 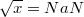 , где
, где 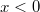
Есть и другие способы получения NaN, подробности можно найти по ссылкам в соответствующем разделе.
По определению NaN ≠ NaN, поэтому, для проверки значения переменной нужно просто сравнить ее с собой.
Бесконечности
В число с плавающей запятой можно записать значение 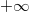 или
или 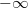 . Как и нули со знаком, бесконечности позволяют получить хотя бы близкий к правильному результат вычисления в случае переполнения. Согласно стандарту IEEE 754 число с плавающей запятой считается равным бесконечности, если все двоичные разряды его порядка - единицы, а мантисса равна нулю. Знак бесконечности определяется знаковым битом числа.
. Как и нули со знаком, бесконечности позволяют получить хотя бы близкий к правильному результат вычисления в случае переполнения. Согласно стандарту IEEE 754 число с плавающей запятой считается равным бесконечности, если все двоичные разряды его порядка - единицы, а мантисса равна нулю. Знак бесконечности определяется знаковым битом числа.
| Знак | |||||||||||||||||
| Порядок | Мантисса | ||||||||||||||||
| 0/1 | 1, | = 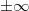 | |||||||||||||||
Получить бесконечность можно при переполнении и при делении ненулевого числа на ноль. При этом 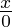
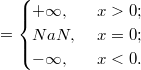
Денормализованные числа
Денормализованные числа (denormalized/subnormal numbers) - это способ увеличить количество представимых числом с плавающей запятой значений около нуля, дабы повысить точность вычислений. Каждое значение денормализованного числа меньше самого маленького нормализованного ("обычного") значения числа с плавающей запятой. Согласно стандарту, если порядок равен своему минимальному значению (все его биты - нули, а истинное значение порядка равно его сдвигу) и все биты мантиссы равны нулю, то это 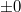 . Если же мантисса не равна нулю, то это число с порядком, на единицу большим минимального (все биты порядка, кроме младшего - нули) и данной мантиссой, целая часть которой считается равной нулю, а не единице.
. Если же мантисса не равна нулю, то это число с порядком, на единицу большим минимального (все биты порядка, кроме младшего - нули) и данной мантиссой, целая часть которой считается равной нулю, а не единице.
То есть число с плавающей запятой, при учете вышесказанного, можно задать следующим образом:
§ 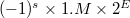 , если
, если 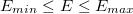 (нормализованное число)
(нормализованное число)
§ 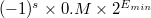 , если
, если 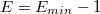 (денормализованное число)
(денормализованное число)
Где  - бит знака,
- бит знака, 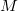 - последовательность битов мантиссы,
- последовательность битов мантиссы, 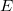 - значение порядка (с учетом сдвига),
- значение порядка (с учетом сдвига), 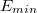 - минимальное значение порядка, используемое для записи чисел (1-сдвиг) ,
- минимальное значение порядка, используемое для записи чисел (1-сдвиг) , 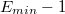 - минимальное значение порядка, которое он в принципе может принять (все биты нули, 0-сдвиг).
- минимальное значение порядка, которое он в принципе может принять (все биты нули, 0-сдвиг).
Хоть денормализованные числа и позволяют бороться с погрешностями и обрабатывать очень маленькие значения, за эти возможности приходится дорого платить. Ввиду сложности денормализованные числа крайне редко реализуют на аппаратном уровне - вместо этого используются программные реализации, работающие значительно медленнее.
В современных процессорах обработка денормализованных чисел происходит в десятки раз медленнее, чем обработка нормализованных чисел. Ниже приведена часть таблицы из статьи Isaac Dooley, Laxmikant Kale "Quantifying the Interference Caused by Subnormal Floating-Point Values" (англ.)
| Производитель | Процессор | Замедление (разы) |
| IBM | PowerPC 970 | 2.4 |
| AMD | Athlon | 6.0 |
| Intel | Pentium 3 | 15.8 |
| AMD | Athlon 64 | 21.4 |
| AMD | Opteron64 | 23.8 |
| Intel | Core Duo | 44.2 |
| Intel | P4 Xeon | 97.9 |
| Intel | Pentium 4 | 131.0 |
| Intel | Itanium 2 | 183.2 |
| Sun | UltraSPARC IV | 520.0 |
В таблице приведены наихудшие результаты тестирования среди всех использованных компиляторов (gcc, icc, xlc) со всеми доступными флагами оптимизации. Исследователи утверждают, что различие среднего случая с худшим незначительно.
Поскольку в стандартных форматах (одинарной и двойной точности) денормализованные числа получаются действительно очень маленькими и практически никак не влияют на результат некоторых вычислений (при этом заметно замедляя их скорость), то иногда они просто игнорируются. При этом используются два простых механизма, получивших называние Flush-to-zero (FTZ) и Denormals-are-zero (DAZ). Первый механизм заставляет операции возвращать ноль, как только становится ясно, что результат будет денормализованным. Второй механизм заставляет операции рассматривать поступающие на вход денормализованные числа как нули.
Ярким примером подобного "отсечения" денормализованных чисел могут послужить видеокарты, в которых резкое падение скорости вычислений в сотню раз недопустимо. Так же, например, в областях, связанных с обработкой звука, нет нужды в очень маленьких числах, поскольку они представляют столь тихий звук, что его не способно воспринять человеческое ухо.
В версии стандарта IEEE 754-2008 денормализованные числа (denormal или denormalized numbers) были переименованы в subnormal numbers, то есть в числа, меньшие "нормальных". Поэтому их иногда еще называют "субнормальными".
