Нормальная и нормализованная форма
Нормальной формой числа с плавающей запятой называется такая форма, в которой мантисса (без учёта знака) в десятичной системе находится на полуинтервале [0; 1). Такая форма записи имеет недостаток: некоторые числа записываются неоднозначно (например, 0,0001 можно записать в 4 формах — 0,0001×100, 0,001×10−1, 0,01×10−2, 0,1×10−3), поэтому распространена также другая форма записи — нормализованная, в которой мантисса десятичного числа принимает значения от 1 (включительно) до 10 (не включительно), а мантисса двоичного числа принимает значения от 1 (включительно) до 2 (не включительно). То есть в мантиссе слева от запятой до применения порядка находится ровно один знак. В такой форме любое число (кроме 0) записывается единственным образом. Ноль же представить таким образом невозможно, поэтому стандарт предусматривает специальную последовательность битов для задания числа 0 (а заодно и некоторых других полезных чисел, таких как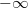 
и 
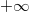). Так как старший двоичный разряд (целая часть) мантиссы вещественного числа в нормализованном виде всегда равен «1», то его можно не записывать, сэкономив таким образом один бит, что и используется в стандарте IEEE 754. В позиционных системах счисления с основанием большим, чем 2 (в троичной, четверичной и др.), этого замечательного свойства нет (ведь целая часть там может быть не только единицей).
| Знак | ||||||||||||||||
| Порядок | Мантисса | |||||||||||||||
| 1, | ||||||||||||||||
Типы чисел с плавающей точкой (по IEEE 754)
Число половинной точности (Binary16, Half precision)
Число́ полови́нной то́чности — компьютерный формат представления чисел, занимающий в памяти половину машинного слова (в случае 32-битного компьютера — 16 бит или 2 байта). В силу невысокой точности этот формат представления чисел с плавающей запятой обычно используется в видеокартах, где небольшой размер и высокая скорость работы важнее точности вычислений.
| Знак | ||||||||||||||||
| Порядок | Мантисса | |||||||||||||||
| 1, | ||||||||||||||||
Порядок записан со сдвигом -15. То есть чтобы получить актуально значение порядка нужно вычесть из него сдвиг. Сдвиг можно получить по формул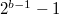е 
, где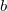 
- число бит, отведенное на хранение порядка (в случае числа половинной точности 
).
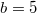Ограничения точности
§ Целые от нуля до 2048 передаются как есть.
§ Целые от 2049 до 4096 округляются к ближайшему чётному целому.
§ Целые от 4097 до 8192 округляются до ближайшего целого, делящегося нацело на 4.
§ Целые от 8193 до 16384 округляются до ближайшего целого, делящегося на 8.
§ Целые от 16385 до 32768 округляются до ближайшего целого, делящегося на 16.
§ Целые от 32769 до 65535 округляются до ближайшего целого, делящегося на 32.
Число одинарной точности (Binary32, Single precision, float)
Число́ одина́рной то́чности — компьютерный формат представления чисел, занимающий в памяти одно машинное слово (в случае 32-битного компьютера — 32 бита или 4 байта). Используется для работы с вещественными числами везде, где не нужна очень высокая точность.
| Знак | |||||||||||||||||||||||||||||||||
| Порядок (8 бит) | Мантисса (23+1 бита) | ||||||||||||||||||||||||||||||||
| 1, | |||||||||||||||||||||||||||||||||
Порядок записан со сдвигом -127.
Число двойной точности (Binary64, Double precision, double)
Число́ двойно́й то́чности — компьютерный формат представления чисел, занимающий в памяти два машинных слова (в случае 32-битного компьютера — 64 бита или 8 байт). Часто используется благодаря своей неплохой точности, даже несмотря на двойной расход памяти и сетевого трафика относительно чисел одинарной точности.
| Знак | |||
| Порядок (11 бит) | Мантисса (52+1 бит) | ||
| 1, | 000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Порядок записан со сдвигом -1023.
Число четверной точности (Binary128, Quadruple precision)
Число́ четверно́й то́чности — компьютерный формат представления чисел, занимающий в памяти четыре машинных слова (в случае 32-битного компьютера — 128 бит или 16 байт). Используется в случае необходимости крайне высокой точности.
| Знак | |||
| Порядок (15 бит) | Мантисса (112+1 бит) | ||
| 1, | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Мантисса (112+1 бит) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0000 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Порядок записан со сдвигом -16383.
Обычно этот формат реализуется программно, случаи аппаратной реализации крайне редки. Также не гарантируется поддержка этого типа в языках программирования, хотя кое-где она и реализована (например, компилятор gcc для архитектуры x86 позволяет использовать тип __float128, являющийся программной реализацией числа с четверной точностью). В совокупности эти факторы делают Quadruple весьма экзотичным и редко встречающимся форматом чисел с плавающей запятой.