Достаточное условие поточечной сходимости тригонометрического

Ряда Фурье

1. Упрошенная запись частичной суммы тригонометрического ряда Фурье

Исследованию поточечной сходимости тригонометрического ряда Фурье предпошлём глубокий анализ поведения частичной суммы ряда Фурье

Этот анализ будет основываться на следующей лемме.

Лемма. последовательности функций

Доказательство.

1)

2)

Отсюда для равномерной сходимости достаточно показать, что следующие последовательности стремятся к нулю.

3) При доказательстве замкнутости тригонометрической системы было установлено:

4) Это и означает, что

Укажем более простой вид частичной суммы ряда Фурье:

непрерывна на

поэтому по лемме получаем

Далее

Итак,

2. Принцип локализации Римана

Последняя запись частичной суммы Фурье называется принципом локализации Римана, согласно которому, сходимость ряда Фурье в точке зависит от значений функции в достаточно маленькой окрестности точки.

3. Достаточное условие поточечной сходимости тригонометрического

ряда Фурье

Можно показать, что для тригонометрических рядов Фурье непрерывных функций отсутствует не только равномерная сходимость, но и поточечная сходимость в отдельных точках.

Теорема.Для любой кусочно непрерывно-дифференцируемой функции f(x) её тригонометрический ряд Фурье сходится всюду, причём к f(x), если точка непрерывности, и к если точка разрыва.

Доказательство.Если то

Покажем, используя (*), что если точка разрыва первого рода, то

Имеем

По формуле Лагранжа

Аналогично:

и для этого т.к. т.е.

Доказано.

ЛЕКЦИЯ 17

Преобразование Фурье. Косинус и синус преобразования Фурье. Свойства преобразования Фурье. Обратное преобразование Фурье

1. Преобразование Фурье. Косинус и синус преобразования Фурье

Пусть дана функция несобственный интеграл от функции 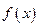, абсолютно сходящийся на всей прямой.

Рассмотрим несобственный интеграл, зависящий от параметра:

называемый преобразованием Фурье функции (это есть аналог коэффициентов Фурье в периодическом случае).

Иногда используют и действительную форму преобразования Фурье, тогда появляются косинус-преобразование Фурье:

и синус-преобразование Фурье:

Обычное преобразование Фурье есть их линейная комбинация:

2. Свойства преобразования Фурье

Лемма 1.Если и интеграл абсолютно сходящийся, то

Доказательство.По соответствующей теореме достаточно проверить равномерную сходимость преобразования Фурье на множестве действительных чисел, т.к.

Воспользуемся признаком равномерной сходимости Вейерштрасса:

сходится. Значит, преобразование Фурье сходится равномерно.

Доказано.

Лемма 2.Если - сходится, то

Доказательство.Также воспользуемся соответствующей теоремой; проверим следующие условия:

1) непрерывность:

2) равномерная сходимость (признак Вейерштрасса):

Следствие.Если сходится, то

Лемма 3. если

Доказательство.

Доказано.

Следствие. если

3. Обратное преобразование Фурье

Саму функцию по её преобразованию Фурье восстанавливают с помощью обратного преобразования Фурье:

аналогично тому, как тригонометрический ряд Фурье восстанавливал периодическую функцию.

Частичные интегралы – это аналог частичных сумм:

И вопрос состоит в следующем: сходится ли при ?

Различают сходимости среднеквадратичную: поточечную: в точке и равномерную:

Пример. Найти преобразование Фурье функции

Замечание. Часто преобразование Фурье определяют формулой

тогда обратное преобразование Фурье имеет вид:

Справедливы следующие утверждения.

Теорема 1.Если 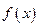абсолютно интегрируема на то

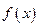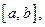Теорема 2.Если абсолютно интегрируема на и кусочно непрерыно-дифференцируема на то

Теорема 3.Если 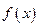абсолютно интегрируема на и непрерывная кусочно непрерывно-дифференцируемая на 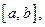то имеет место равномерная сходимость

Библиографический список

Основная литература

1. Ильин В.А., Поздняк Э.Г. Основы математического анализа. М.: Физматлит, Ч.1, 2002. – 646с., Ч. 2, 2002. – 447с.

2. Зорич В.А. Математический анализ. М.: МЦНМО, Ч.1, 2002. – 657с., Ч. 2, 2002. – 787с.

3. Кузнецов, Л. А. Сборник заданий по высшей математике. Типовые расчеты : учеб. пособие для вузов / Л. А. Кузнецов .— 10-е изд., стер. — СПб. ; М. ; Краснодар : Лань, 2008 .— 240 с.

4. Глаголев В.В., Иванов В.И., Смирнов О.И., Горбачев Д.В. Сборник заданий по математическому анализу. Типовые расчеты с приме­рами решений. Ч. 1. Тула: ТулГУ, 2007. – 172с.

5. Глаголев В.В., Иванов В.И., Смирнов О.И. Сборник заданий по математическому анализу. Типовые расчеты. Тула: ТулГУ, 2010. – 96с.

Дополнительная литература

1. Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу. М.: Дрофа, 2004. – 640с.

2. Виноградова И.А., Олехник С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу. М.: Высшая школа, Кн.1, 2002. – 728с., Кн.2, 2002. – 712с.

3. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: АСТ, 2007. – 560с.

4. Золотухин А.Я. Элементы теории множеств, меры и интеграла Лебега. Тула: ТулГУ, 2007. – 107с.

5. Рудин У. Основы математического анализа. СПб.: Лань, 2004. – 320с.

Периодические издания

1. Вестник МГУ. Серия 1. Математика. Механика. — М.: МГУ.— ISSN 0579-9368.