Виды временных рядов, цели и методы их анализа.

Временные ряды различают по нескольким категориям, в соответствии с которыми они делятся на следующие виды:

А. «Стационарные временные ряды»,характеристики которых (среднее значение, дисперсия и т.д. уровней ряда) не изменяются во времени, и«нестационарные временные ряды»; (статистики различают понятия «стационарные временные ряды в узком и в широком смысле», но мы ограничимся лишь общим представлением).

Б. «Моментные временные ряды», уровни которых характеризуют значения показателя по состоянию на определенные моменты времени или по № в порядке представления,и «интервальные временные ряды», уровни которых характеризуют значение показателя за определенные интервалы времени, например, ряд среднесуточного производства продукции). Важная особенность интервальных временных рядов абсолют­ных величин заключается в возможности суммирования их уров­ней («свойство аддитивности»). В результате этой процедуры получаются накопленные ито­ги, имеющие осмысленное содержание. Например, от рядов среднесуточной производительности можно переходить к рядам еженедельного, месячного, годового производства. Моментные временные ряды, например размер детали, в отличие от интервальных свойством аддитивности не обладают и их суммирование не имеет смысла.

В. Уровни временного ряда могут быть «абсолютные» (непосредственно наблюдаемые значения) и «производные»,вычисляемые на основе абсолютных показателей. К «производным уровням временного ряда» относятся, в частности, относительные и средние значения, значения, полученные в результате рассмотренных ниже процедур сглаживания, исключения систематических составляющих (см. § 8.2 - 8.3). Кроме того, к «производным уровням временного ряда» относятся, например, характеристики технологии производства или качества продукции, рассчитанные на основе ранее установленных их связей с «абсолютными показателями», определяемыми контрольными приборами.

Цели анализа временных рядов:

- краткое (сжатое) описание характерных особенностей ряда;

- подбор статистической модели (моделей), описывающей вре­менной ряд;

- предсказание будущих значений на основе прошлых наблюдений;

- разработка технических рекомендаций по совершенствованию наблюдаемых тенденций, то есть управление процессом, порождающим временной ряд.

8.2. Преобразование непрерывно получаемых данных во временной ряд

При экспериментальном исследовании процессов их характеристики часто записываются в виде непрерывных функций. Они могут иметь вид аналогового сигнала, непосредственно поступающего с датчика в виде изменений во времени напряжения электрического тока, могут наблюдаться непосредственно на экране монитора компьютера или в виде записи на бумажной ленте.

Чтобы преобразовать непрерывную функцию во временной ряд, готовый для последующего анализа, необходимо произвести целую последовательность операций.

1. Редактирование, заключающееся в выявлении и исключении аномальных и (или) искажённых сигналов, которые могут возникать при сборе и регистрации данных, например, за счёт высокого уровня помех, снижения уровня сигнала, исчезновения сигнала при плохой работе датчика и т.д. Редактирование часто сводится просто к визуальному анализу данных опытным специалистом. Следует отметить, что редактирование данных перед их цифровой обработкой очень важно, т.к. после преобразования данных в цифровую форму, как правило, бывает трудно обнаружить даже самые очевидные ошибки в исходном сигнале.

2. Дискретизация. Это процесс определения точек (т.е. моментов времени), в которых должны быть произведены выборки значений. Дискретизация при цифровой обработке данных обычно производится через равные интервалы времени, как показано на рис. 5.1. Задача заключается в правильном выборе величины «интервала дискретности» h (этот интервал иногда называют периодом опросов, или интервалом выборок). При слишком близко расположенных друг к другу точках число полученных данные будет избыточно велико, что неизбежно вызовет увеличение как объёма, так и стоимости расчётов. При слишком большом h возможно явление «маскировки» (наложения) частот, когда высокие частоты оказываются «замаскированными» и могут не идентифицироваться.

.

-

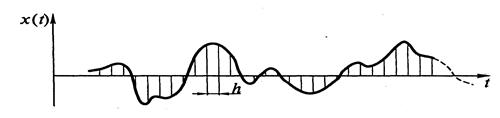
Рис. 5.1. Дискретное представление непрерывной функции

3. Квантование, то есть преобразование отсчётов, сделанных в соответствующие моменты времени, в цифровую форму. Числовое значение каждого отсчёта должно быть выражено некоторым конечным числом цифр. То есть задача заключается в том, чтобы приближённо описать бесконечную последовательность возможных значений непрерывного процесса с помощью конечного числа уровней квантования. Если квантование выполнено верно, то истинным значениям исходного непрерывного сигнала будут соответствовать наиболее близкие к ним уровни квантования, рис. 5.2.

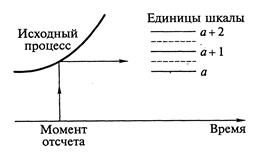
Рис. 5.2. Ошибка квантования:  - уровни квантования; ------ - промежуток между уровнями, определяющий ошибку квантования

На практике ошибка квантования обычно пренебрежимо мала по сравнению с другими ошибками, возникающими в процессе сбора и обработки данных. Как видно из рис. 5.2, она не должна превышать единицы шкалы квантования.

4. Изменение формата часто оказывается совершенно необходимой операцией. Действительно, устройства ввода современных компьютеров приспособлены для приема данных, записанных только в определённом формате, который может не обеспечиваться системой преобразования аналогового сигнала в цифровой.

5. Преобразование данных, записанных в дискретном виде, в реальные физические единицы. Как правило, зависимость между физическими единицами и цифровыми данными линейна. Поэтому операция обычно не представляет трудности.

Компоненты временных рядов.

Уровни ряда могут принимать только «детерминированные» или только «случай­ные» значения, но, как правило, представляют собой наложение, результат взаимодействия детерминированныхи случай­ных составляющих.

Под детерминированной (закономерной) соста­вляющей временного ряда x₁,... x_i, ,x_n понимают числовую последовательность, элементы которой вычисляются по определенному правилу как функция текущей переменной 1…i,...,n.

Детерминированная составляющая вызвана действием ограниченного количества определенных факторов или причин. В зависимости от особенностей действия этих факторов детерминированная соста­вляющая временного ряда может в свою очередь состоять из двух компонент:

- «тренд» - плавно изменяющаяся, не циклическая компонента, описывающая влияние долговременных факторов, эффект которых копится постепенно;u_i

- составляющая временного ряда, описывающая влияние факторов, эффект которых носит периодический циклический характер;v_i. Заметим, что периоды колебания каждого из действующих факторов могут различаться и результат их совместного действия может иметь сложный, трудно описываемый характер.

Факторы, под действием которых формируется «случай­ная компонента» ε, разделяют на два вида:

1. факторы резкого, внезапного действия (например, стихийные бедствия, в металлообработке - поломка установки, отключение питания и т.д.);

2. случайныеколебания, являющиеся результатом действия большого числа побочных факторов. Влияние каждого из таких факторов незначительно, но ощутимо их суммарное воздействие. (Именно действия большого числа такого рода факторов, как правило, приводят к нормальному распределению случай­ной компоненты.)

Таким образов, мы выделили три основные компоненты: две детерминированные u_i + v_i и одна случайная ε. Если временной ряд представляется в виде суммы соответствующих компонентy_t = u_i + v_i + ε, то полученная модель носит название «аддитивной», если в виде произведения y_t = u_i · v_i · ε,- «мультипликативной». Можно также выделить модели - «смешанного типа», напримерy, = u_i · v_i + ε. Отличительная особенность аддитивной модели заключается в том, что амплитуда периодическихколебаний остается примерно постоянной, неизменной во времени. Наоборот, о мультипликативном характере модели говорит возрастание амплитуды колебаний, см. рис. 8.1.

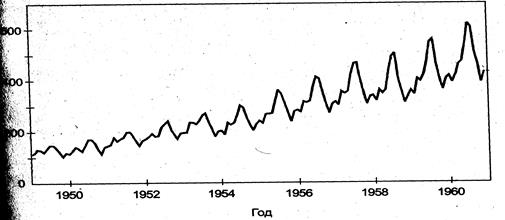
Рис. 8.1 графическое представление «мультипликативной» модели

Анализ временных рядов