T- тесты о равенстве средних значений

Строго говоря, описанные ниже критерии применимы только к выборкам, извлеченным из генеральной совокупности, распределённой по нормальному закону. Однако специальные исследования показали, что рассматриваемый в этом параграфе t-критерий является весьма устойчивым по отноше­нию к отклонениям исследуемых генеральных совокупностей от нормаль­ного закона распределения. Это позволяет широко использовать его в заводской практике, когда, как правило, нет возможности предварительно проводить достаточно трудоёмкую проверку нормальности исследуемых генеральных совокупностей (см. ниже § 7.6). Следует лишь иметь в виду, что истинные значения уровня значимости и мощности критерия могут незначительно отличаться от заданных значений.

Данный параграф посвящен процедурам проверки гипотез о равенстве средних (математических ожиданий) двух нормальных распределений X и Y с неизвестными дисперсиями σ_X и σ_Y. Причем можно выдвинуть два предпо­ложения:

1) обе дисперсии неизвестны, но предполагается, что они рав­ны между собой (σ_X = σ_Y).

2) обе дисперсии неизвестны, их равенство не предполагается (σ_X ≠ σ_Y).

В первом случае переходят к объединенной оценке дисперсии S²:

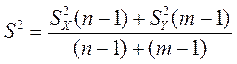(7.8)

В математической статистике доказывается, что если гипотеза о равенстве средних значений 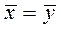выполняется, то определяемая с использованием оценки стандартного отклонения объединенной дисперсии (7.8) величина

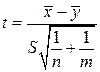(7.9)

имеет распределение Стьюдента с k= n+m-2 степенями сво­боды, т.е.

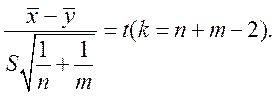
Величину t используют в качестве критерия при проверке ги­потезы H₀: .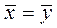

Когда дисперсии неизвестны и их равенство не предполага­ется (σ_X ≠ σ_Y), то взамен формулы (7.9) используется аналог t-статистики с заменой неизвестных дисперсий их оценками S_X и S_Y, называ­емый критерием Фишера-Беренса:

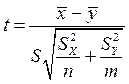(7.10)

Известно, что это распределе­ние близко к распределению Стьюдента с числом степеней свобо­ды, равным

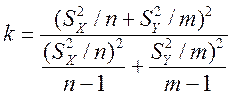
Аналогично двум рассмотренным аналитическим подходам в программе excel имеется два инструмента для случаев, когда σ_X = σ_Y и когда σ_X ≠ σ_Y. Окна инструментов «Двухвыборочный t-тест с одинаковыми дисперсиями» (рис. 7.9) и «Двухвыборочный t-тест с различными дисперсиями» аналогичны по своей структуре. Они содержат опцию «Гипотетическая средняя разность», в которую при проверке равенства средних можно ничего не вносить, если эта «Гипотетическая средняя разность» равна нулю (см. выше).

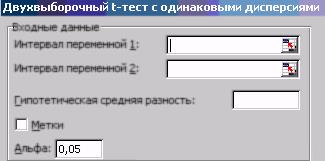
Рис. 7.9. Двухвыборочный t-тест с одинаковыми дисперсиями

В выходных данных кроме значений средних, дисперсий, количества наблюдений для каждой из двух выборок присутствуют:

- гипотетическая разность средних;

- число степеней свободы df = n₁+n₂-2;

- вычисленное значение t-статистики;

- значения «t критическое одностороннее» и «t критическое двухстороннее», соответственно для односторонней и двухсторонней гипотезы;

- вероятности P(T<=t) выполнения односторонней и двухсторонней гипотезы о равенстве средних.

Вычисленное значение t-статистики следует сравнивать со значениями «t критическое одностороннее» или «t критическое двухстороннее» в зависимости от того, какая альтернативная гипотеза (односторонняя или двухсторонняя) рассматривается. При t > t_{критическое} гипотеза о равенстве средних отвергается, при t < t_{критическое} гипотеза о равенстве средних подтверждается.

Значение P для двухсторонней гипотезы можно сравнивать с принятым уровнем значимости α.