Систематизация, статистический анализ данных, контроль и управление производственными
СИСТЕМАТИЗАЦИЯ, СТАТИСТИЧЕСКИЙ АНАЛИЗ ДАННЫХ, КОНТРОЛЬ И УПРАВЛЕНИЕ ПРОИЗВОДСТВЕННЫМИ
ПРОЦЕССАМИ
Рекомендовано
Учёным советом Вятского государственного
университета в качестве
учебного пособия
Киров
Печатается по решению редакционно-издательского совета
Вятского государственного университета
ББК 34.5 + 22.172
П23
Рецензент: доктор технических наук, старший научный сотрудник, ведущий специалист ФГУП «НПЦ газотурбостроения «Салют», г. Москва С.Г. Хаютин
Певзнер, М.З. Систематизация, статистический анализ данных, контроль и управление производственными процессами: курс лекций / М.З. Певзнер. - Киров : Изд-во ВятГУ, 2012. - 165 с.
Курс лекцийвключает сведения из теории статистики, в частности законы и характеристики рассеяния непрерывных и дискретных случайных величин, проверки статистических гипотез, анализа временных рядов и статистического управления качеством продукции, а также способы и технические приёмы по решению рассматриваемых задач с использованием современных программных средств.
Рекомендуется для студентов специальности 151001 (120100) «Технология машиностроения» по дисциплинам «Математическая обработка экспериментальных данных», «Прикладная статистика» и «Основы научных исследований».
Редактор А.В. Куликова
Подписано в печать Усл. печ. л. 4,4
Бумага для офисной техники Печать цифровая
Заказ № Тираж 50 экз. Бесплатно
Текст напечатан с оригинала-макета, представленного автором
610000, г. Киров, ул. Московская, 36
Оформление обложки, изготовление ПРИП ВятГУ
© Певзнер М.З., 2012
© Вятский государственный университет, 2011
Оглавление
Оглавление ……………………………………………………………………3
Введение……………………………………………………………………….8
Глава 1. Основные понятия прикладной математической
статистики………………………………………………………………….10
1.1 Случайные величины и их классификация. …………………….…….11
1.2 Области и методы математической статистики………………………16
1.3 Генеральная совокупность и выборка. ……………………………..17
1.4 Основы использования программы MS EXCEL при статистической
обработке случайных данных. …………………………………….……..18
1.4.1 Установка пакета анализа…………………………………………...18
1.4.2 Обзор инструментов анализа и статистических функций. ……….22
1.4.3 Примеры работы со статистическими функциями (СЧЁТ и
родственные ей функции) и инструментами анализа («Выборка»). 25
1.5. Вопросы и задания к главе 1………………………………………26
1.6 Дополнительная литература к главе 1……………………………..27
Глава 2 Распределение случайных величин. …………………………29
2.1 Представления эмпирических распределений.………………………29
2.2 Плотность и интегральная функция .…………………………………32
2.3 Ранжирование статистических данных в программе MS EXCEL….35
2.3.1 Определение экстремальных значений…………………………….35
2.3.2. Статистические функции РАНГ и ПРОЦЕНТРАНГ………………36
2.3.3. Функция ПЕРСЕНТИЛЬ………………………………………………38
2.3.4. Инструмент анализа «Ранг и персентиль»…………………………..39
2.4 Представление эмпирических и теоретических распределений
в программе MS EXCEL……………………………………………………..40
2.5 Вопросы к главе 2………………………………………………….…..44
Глава 3 Точечные оценки рассеяния случайных величин…………46
3.1 Требования к точечным оценкам. ……………………. ……………..47
3.2 Точечные оценки положения, степени и характера рассеяния случайной величины на числовой оси………………………………………………..47
3.3 Представление о моментах случайных величин и их свойствах….. 53
3.4 Статистическиефункции и инструмент программы MS EXCEL
«Описательная статистика», определяющие точечные оценки……….56
3.5 Вопросы и задания к главе 3……………………………………………..61
3.6 Дополнительная литература к главе 3…………………………………...61
Глава 4 Выборочные методы контроля…………………………………..63
4.1 Способы формирования выборок………………………………………..63
4.2 Ошибка и необходимый объем выборки……………………………….64
4.3 Способы обнаружения и исключения «выбросов»……………………68
4.4 Планы выборочного контроля…………………………………………..75
4.5. Вопросы и задачи к главе 4.
Глава 5 Основные законы распределения случайных величин…….77
5.1 Нормальное и стандартное нормальное распределение……………….77
5.2 Другие непрерывные распределения…………………………………….81
5.3 Основные дискретные распределения…………………………………89
5.4 Средства программы MS EXCEL, определяющие законы
непрерывного и дискретного распределения.………………………….. 92
5.4.1 Методология работы в программе MS EXCEL с функциями
нормального распределения и распределения Стьюдента ………………93
5.4.2 Инструмент анализа «Генерация случайных чисел» …………….98
5.5. Вопросы и задачи к главе 4……………………………………..…..101
5.6 Дополнительная литература к главе 4……………………………..…102
Глава 8 Современные интеллектуальные информационные системы и программные средства
9.1 Представление и классификация интеллектуальных информационных систем (ИИС) - Романов
9.2 Нейронные сети
9.3 Программа STATISTICA
Введение
Величины, которые контролируются в производственных процессах (технологические параметры, характеристики качества), представляют собой не постоянные и не детерминированные значения, которые можно точно измерить или точно рассчитать, аслучайные величины. Их можно проконтролировать или определить лишь с определённой степенью точности. Поэтому правила арифметики или алгебры для операций с этими величинами не в полной степени пригодны - здесь требуется использование законов, основанных на теории вероятности и математической статистике. Эта область математики постоянно развивается [ ], особенно её практические приложения (прикладная статистика) [ ]. Совершенствуются и методы обработки данных во всех отраслях знаний [ ], что в первую очередь связано с совершенствованием средств анализа (машинной техники и программных средств) [ ].
Для того, чтобы правильно ориентироваться в окружающих нас случайных величинах, уметь правильно оценивать эти величины и оперировать ими, необходимо знать основные области и методы математической статистики. И это знание совершенно необходимо для решения множества вопросов, встречающихся в производственной практике. В частности, раздел прикладной статистики, занимающийся анализом последовательно контролируемых данных (характеристик технологии, качества) играет особую роль в анализе и управлении процессами, т.к. является основой принципов и методов всеобщего управления качеством (TQM),
К сожалению, в отличие от многих западных стран математическая статистика не входит в школьную программу, а курс, преподаваемый в ряде ВУЗов в совокупности с теорией вероятности, носит весьма отвлечённый характер, далёкий от нужд прикладной статистики в конкретной отрасли знаний. Задачей настоящего курса является восполнение отмеченного пробела, выработка у студентов "статистического мышления" и овладение основными статистическими методами, используемыми для решения инженерных технологических задач..
В предлагаемом курсе рассмотрены следующие темы.
1. Классификация случайных величин.
2. Законы распределения случайных величин.
3. Выборочные методы, используемые для контроля множеств случайных величин.
4. Точечные и интервальные оценки рассеяния.
5. Статистические гипотезы о соотношении, величине, степени рассеяния и законах распределения случайных величин; методы проверки гипотез.
6. Представление о временных рядах, их классификации, стационарности и эргодичности, разложении на составляющие.
7. Контрольные карты как основной инструмент статистического управления качеством продукции.
8. Функции и инструменты программы MS Excel, предназначенные для следующих направлений статистического анализа:
- выборочные методы исследования генеральной совокупности;
- определения точечных и интервальных оценок;
- установления интегральной функции и плотности для различных законов распределения непрерывных и дискретных случайных величин;
- проверки статистических гипотез о равенстве дисперсий, средних значений выборок и их соответствии теоретическим законам распределения случайных величин;
- сглаживания, гармонического анализа временных рядов и статистического контроля производственных процессов.
9. Знакомство с программой statistica и основными понятиями интеллектуальных информационных систем.
Глава 1. Основные понятия прикладной математической статистики.
Прикладная статистика это техническая дисциплина, основанная на теории вероятностей и математической статистике и посвященная методам сбора, анализа и обработки статистических данных для научных и практических целей в конкретной области знаний.
Методы прикладной статистики разработаны применительно ко многим областям знаний (медицине, психологии, очень развиты в экономике и, конечно, в технике) и в основном сходны, т.к. основаны, по сути, на одном аппарате математической статистики. Но в каждой области знаний имеют свою специфику, зависящую от способов извлечения и характера обрабатываемых данных.
В частности, в технике каждая из случайных величин, с которыми мы имеем дело (технологические факторы, размеры, механические свойства и иные характеристики деталей, производительность и т. д.), имеет своё особое распределение (колебание относительно среднего значения). При этом все они в совокупности в зависимости от особенностей каждого исследуемого процесса формируют своеобразное многомерное пространство.
Математическая статистика сформировалась как наука в 19 - начале 20 века. Но годом её рождения можно считать 1794г., когда великий математик Карл ФридрихГаусс разработал основополагающий метод наименьших квадратов. К нашей гордости следует отметить, что научно-теоретическая база математической статистики создавалась, в частности, отечественными учёными (академики М.В. Остроградский, А.Н. Колмогоров, Л.В. Канторович). Известно, что благодаря усилиям Михаила Васильевича Остроградского, элементы математической статистики по-видимому, впервые в мире использовались при приёмке продукции на российских оружейных заводах ещё в 19 веке! В настоящее время математическая статистика является неотъемлемым элементом международных стандартов ISO, требующих привлечения методов статистического контроля качества (SQC) и статистического управления процессами (SPC). Применение этих международных стандартов и их многочисленных отечественных аналогов (рис. 1.1) обязательно для выполнения на территории РФ и является показателем правильного функционирования на предприятии системы менеджмента качества и, следовательно, конкурентоспособности продукции на отечественном и зарубежном рынке.
Установка пакета анализа
Установка надстройки «Пакет анализа» в Microsoft Office EXCEL 2003.Для того чтобы отыскать команду вызова надстройки «Пакет анализа», необходимо воспользоваться меню «Сервис». Здесь возможны следующие ситуации.
1. В меню «Сервис» имеется команда «Анализ данных», позволяющая сразу вызвать окно доступных инструментов анализа.
2. В меню «Сервис» отсутствует команда «Анализ данных». В этом случае необходимо в меню «Сервис» выполнить команду «Надстройки». Раскроется одноименное окно (рис. 1.5) со списком доступных надстроек. В этом списке нужно найти элемент «Пакет анализа», поставить рядом с ним «галку» и выполнить команду ОК. Если надстройка «Пакет анализа» была инсталлирована (стандартная установка), то в меню Сервис появится команда «Анализ данных». (В случае возможного исчезновения пункта «Анализ данных» в меню «Сервис» при наличии «Пакета анализа» в меню «Сервис» - «Надстройки» для его восстановления необходима перезагрузка компьютера.)
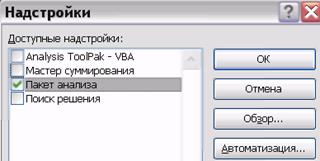
Рис. 1.5. Окно «Надстройки»
3. В списке окна «Надстройки» нет элемента «Пакет анализа». В этом случае необходимо заново произвести доустановку MS EXCEL.
Установка надстройки «Пакет анализа» в Microsoft Office EXCEL 2007.В Microsoft Office 2007 для включения «Пакета анализа» необходимо выполнить следующие действия.
1. Нажать «Настройка панели быстрого доступа» (маленький треугольник в строке меню).
2. Выбрать «Другие команды» (см. рис. 1.6).
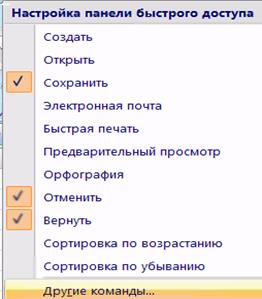
Рис. 1.6. Начальный этап настройки панели быстрого доступа
3. Выбрать вкладку «Данные» (рис. 1.7). (К этой вкладке можно перейти быстрее, нажав правой кнопкой мыши на «Office».)
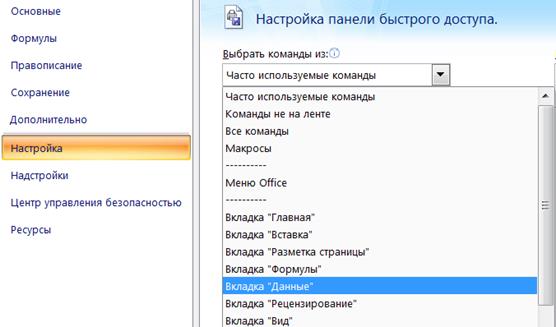
Рис. 1.7. Выбор вкладки «Данные»
4.Перейти от «Настройка» к «Надстройки» и нажать кнопку «Перейти» (рис. 1.8).
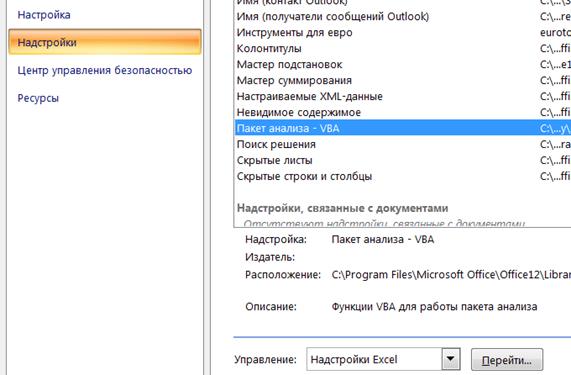
Рис. 1.8. Выбор «Пакета анализа» в «Надстройках»
6. В окне «Доступные надстройки» установить флажок «Пакет анализа» и нажать кнопку ОК.
7. После загрузки пакета анализа в меню «Данные» становится доступной команда «Анализ данных».
Если «Пакет анализа» отсутствует в списке поля «Доступные надстройки», то для проведения поиска необходимо нажать кнопку «Обзор». В случае появления сообщения о том, что пакет статистического анализа не установлен на компьютере и предложения установить его, следует нажать кнопку «Да».
Примеры работы со статистическими функциями (СЧЁТ и родственные ей функции) и инструментами анализа («Выборка»).
Функция СЧЁТ - наиболее простая в ряду подсчитывающих функций, использующаяся для определения количества числовых ячеек в интервалах или массивах ячеек. Учитываются аргументы, которые являются числами, пустыми значениями, логическими значениями, датами или текстами, изображающими числа. Аргументы, являющиеся значениями ошибки или текстами, которые нельзя интерпретировать как числа, игнорируются. Если аргумент является массивом или ссылкой, то подсчитываются только числа в этом массиве или ссылке. Пустые ячейки, логические значения, тексты и значения ошибок в массиве или ссылке игнорируются. Наоборот, функция СЧЁТЗ используется для подсчёта количества непустых значений в списке аргументов или количества ячеек с данными в интервале или массиве. Кроме того, имеется функция СЧИТАТЬПУСТОТЫ, которая подсчитывает количество пустых ячеек в заданном диапазоне.
Из данной серии родственных функций наиболее полезна функция СЧЁТЕСЛИ - она подсчитывает количество ячеек, удовлетворяющих заданному критерию. Например, критерий «>k» позволит подсчитывать количество ячеек со значением выше k. (Microsoft EXCEL предлагает дополнительные функции, которые можно применять для анализа данных с использованием условий; например, для вычисления суммы значений, попадающих в интервал, заданный текстовой строкой или числами, можно использовать функцию «СУММЕСЛИ» из категории «Математические»; для получения формулы, выбирающей в зависимости от выполнения условия одно из двух значений, можно использовать функцию «ЕСЛИ» из категории «Логические»).
Инструмент «Выборка» (рис. 1.12) создает выборку из генеральной совокупности («входной интервал»). Он позволяет получать как механическую (метод выборки «периодический»), так и случайную (причём «повторную») выборку. Под «Числом выборок» следует понимать задаваемый объём n выборки, а в элемент «Метки» (здесь и в других инструментах анализа данных) следует поставить «галку», если массивы данных задаются с их названиями. При избрании в качестве «параметров вывода» «выходного интервала» произведённая выборка будет записана в виде одного столбца, начиная с ячейки, указанной в ссылке.
Рис. 1.12. Инструмент анализа данных «Выборка»
1.5. Вопросы и задания к главе 1
1.1. Какие типы случайных величин Вы знаете?
1.2. Как классифицируются случайные величины?
1.3. Классифицируйте области и методы математической статистики.
1.4. Что называют случайной выборкой, объемом выборки, элементом выборки?
1.5. Что называют генеральной совокупностью?
1.6. Сделайте доступным пакет анализа данных в используемом Вами офисе.
1.6 Дополнительная литература к главе 1.
1. ГОСТ Р 50779.0-95. Статистические методы. Основные положения. - Дата введения 1996-07-01. - М.: Госстандарт России, 1995. - 12 с.
2. ГОСТ Р 50779.10-2000 (ИСО 3534.1-93). Статистические методы. Вероятность и основы статистики. Термины и определения. - Введ. 2001-07-01. - М.: Госстандарт России, 2001. - 35 с.
3. Рекомендации по стандартизации. Статистические методы. Руководство по выбору статистических методов для стандартов и технических условий. Р 50.1.059-2006. - М.: Стандартинформ, 2007. - 24 с.
4. ГОСТ Р 50779.70-99 (ИСО 2859.0-95). Статистические методы. Процедуры выборочного контроля по альтернативному признаку. Часть 0. Введение в систему выборочного контроля по альтернативному признаку на основе приемлемого уровня качества AQL. - Введ. 2000-07-01. - М.: Изд-во стандартов, 2000. - 53 с.
5. ГОСТ 18321-74. Статистический контроль качества. Методы случайного отбора выборок штучной продукции. - Введ. 01.01.1974. - М.: Изд-во стандартов, 1974. - 12 с.
6. Вуколов Э.А. Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов STATISTICA и EXCEL. - М.: ФОРУМ; ИНФРА-М, 2004. - 464 с. - (Профессиональное образование).
7. Саймон Д. Анализ данных в Excel: наглядный курс создания отчетов, диаграмм и сводных таблиц: пер. с англ.. - М.: Издательский дом "Вильямс", 2004. - 528 с.
8. Берк К., Кэйри П. Анализ данных с помощью Microsoft Excel. - М.: Издательский дом "Вильямс", 2005. - 560 с.
9. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере / под ред. В.Э. Фигурнова. - М.: ИНФРА-М, 2008.. - 528 с.
10. Певзнер, М.З. Освоение инструментов анализа и статистических функций программы MS EXCEL на примерах решения задач предварительной обработки данных : учебное пособие / М.З. Певзнер, А.Я. Часников. - Киров : Изд-во ВятГУ, 2011. - 43 с.
Функция ПЕРСЕНТИЛЬ
Функция ПЕРСЕНТИЛЬ (рис. 2.9) в определённом отношении решает задачу, обратную функции ПРОЦЕНТРАНГ. Она используется для определения некоторого значения из набора данных (не более 8191 значений), соответствующего заданному относительному положению этого значения. Причём это относительное положение изменяется в следующих пределах: наименьшее значение имеет персентиль 0, а наибольшее значение - персентиль 1. Функция ПЕРСЕНТИЛЬ может служить для определения некоторого порога приемлемости. Например, нужно принять в институт наилучших кандидатов (90 %); если кандидатов больше, чем имеющихся мест, нужно выбрать только тех, которые набрали баллов более, чем 0,9-я персентиль.
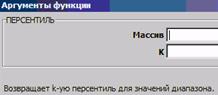
Рис. 2.9. Аргументы функции ПЕРСЕНТИЛЬ, где k - значение персентиля в интервале от 0 до 1 включительно
Применительно к анализу производственных процессов бывает целесообразно не принимать к рассмотрению те результаты контроля, которые слишком далеки от среднего значения (настолько, что могут относиться к «выбросам»). Для этого, например, принимается решение отбросить результаты, имеющие значение персентиля больше 0,95 и меньше 0,05. Тогда в поле «к» (см. рис. 2.9) следует последовательно ставить 0,95 (95-й персентиль) и определять максимально допустимое значение результатов контроля, а затем - 0,05 (5-й персентиль), определяя минимально допустимое значение результатов контроля.
Вопросы к главе 2
1. Что называют статистическим рядом?
2. Что называют вариационным рядом случайной выборки?
3. Что такое интервальный статистический ряд?
4. Что такое выборочные распределения?
5. Дайте определение эмпирической плотности распределения.
6. Что такое гистограмма?
7. Что такое полигон частот?
8. Укажите связь между функцией распределения случайной выборки и функцией распределения генеральной совокупности.
9. Объясните геометрически и аналитически связь между функцией плотности и интегральной функцией распределения.
10. Изобразите, как могут выглядеть функция плотности и интегральная функция непрерывного, дискретного и смешанного распределения.
11. В чём разница функций МАКС и НАИБОЛЬШИЙ?
12. В чём сущность функции ПЕРСЕНТИЛЬ?
13. Назовите комбинацию клавиш для вывода интервала частот.
14. Какую роль играет аргумент "Интегральный"?
Требования к точечным оценкам.
Для того чтобы оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям, а именно: должны быть несмещёнными, эффективными и состоятельными.
Несмещённаяоценка в среднем совпадает с истинным значением оцениваемого параметра.
Эффективная оценка характеризуется минимальной дисперсией в сравнении со всеми другими несмещёнными оценками.
Состоятельная оценка с ростом объёма выборки приближается к истинному значению оцениваемого параметра.
Положительная асимметрия указывает на отклонение распределения в сторону положительных значений (вправо по числовой оси). Отрицательная асимметрия указывает на отклонение распределения в сторону отрицательных значений.
Эксцесс (обозначается Е или ε) характеризует степень выраженности «хвостов» распределения, т.е. частоту появления значений, удаленных от математического ожидания. Для нормального распределения эксцесс, определяемый по формуле (3.12), равен 3, а при расчёте по формуле для выборки (3.14) за счёт дополнительно введённого второго члена - нулю. (Таким же образом он рассчитывается в программе EXCEL, см. § 2.2). В результатеотносительно более «остроконечное», чем нормальное распределение имеет положительный эксцесс, а относительно более «сглаженное» - отрицательный эксцесс (рис 3.4).
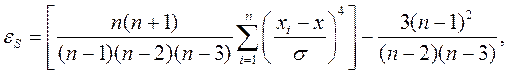(3.14)
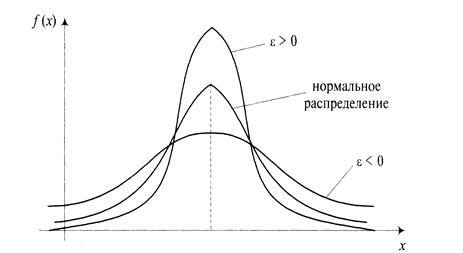
Рис. 3.4. Схематическое изображение распределения с положительным и отрицательным эксцессом
Рис. 3.8. Инструмент анализа «Описательная статистика»
С помощью инструмента «Описательная статистика» для каждого из множества массивов данных, сгруппированных по строкам или столбцам, можно вычислить и вывести на экран следующие параметры:
- среднее (статистическую оценку математического ожидания) по формуле (3.1);
- стандартную ошибку среднего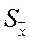 
(«Стандартная ошибка») по формуле (3.7);
- медиану (Ме);
- моду (Мо);
- дисперсию выборки по формуле (3.3);
- СКО по формуле (3.5);
- эксцесс по формуле (3.14);
- асимметрию (СКОС) по формуле (3.13);
- размах выборки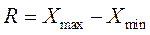 
(«Интервал»);
- минимальное значение выборки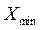 
(«Минимум»);
- максимальное значение выборки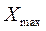 
(«Максимум»);
- сумму всех значений выборки («Сумма»);
- объём выборки n («Счет»);
- «Наибольший(k)» и «Наименьший(k)», см. ниже и соответствующие функции в § 2.3.1;
- «уровень надежности» (предельную ошибку выборки) для заданной доверительной вероятности: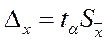 
,
где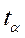 
- параметр распределения Стьюдента (см. § 5.2), определяемый по «уровню значимости» (называется также «коэффициент риска» и обозначается α или β) и «числу степеней свободы» (обозначается k или f) k = n - 1; 
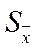- стандартная ошибка среднего.
Инструмент «Описательная статистика» (см. рис. 3.8) предлагает следующие параметры вывода:
«Итоговая статистика». Если в этом поле стоит флажок, то производится расчет всех указанных выше параметров кроме последних трёх;
«Уровень надежности». Если флажок стоит в этом поле, то производится расчет уровня надёжности (предельной ошибки выборки)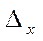 
(см. выше) и результат выводится в нижней части итоговой таблицы (необходимо указать значение доверительной вероятности в процентах, по умолчанию выводится 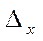для доверительной вероятности 95 %);
«К-й наименьший» и «К-й наибольший». Если это поле помечено флажком, то производится определение значений в выборке к-ого в порядке увеличения и к-ого в порядке уменьшения. (По умолчанию стоит к = 1 и определяются максимальные и минимальные значения в выборках.)
3.5 Вопросы и задания к главе 3
1. Назовите и сформулируйте сущность требований к точечным оценкам
2. Приведите формулы оценок дисперсий и стандартных отклонений.
3. Объясните понятия «квартиль» и «квантиль»
4. Как определяются погрешности оценок выборочных среднего и СКО?
5. На примере нормального распределения покажите, как изменяется форма распределения при положительных и отрицательных значениях асимметрии и эксцесса.
3.6 Дополнительная литература к главе 3.
1. ГОСТ Р 50779.21-2004. Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть I. Нормальное распределение. - Введ. 2004-06-01. - М.: Изд-во стандартов, 2004. - 24 с.
2. ГОСТ Р 50779.22-2005 (ИСО 2602 : 1980). Статистические методы. Статистическое представление данных. Точечная оценка и доверительный интервал для среднего. - Введ. 2005-07-01. - М.: Стандартинформ, 2005. - 3 с.
3. ГОСТ Р 50779.24-2005 (ИСО 8595 : 1990). Статистические методы. Статистическое представление данных. Оценка медианы. - Введ. 2005-07-01. - М.: Стандартинформ, 2005. - 3 с.
4. ГОСТ Р 50779.25-2005 (ИСО 3494:1976). Статистические методы. Статистическое представление данных. Мощность тестов для средних и дисперсий. - Введ. 2006-01-01. - М.: Стандартинформ, 2005. - 79 с.
5. Годин А. М., Статистические средние и другие величины и их применение в различных отраслях деятельности [Текст] - 2009. - 251 с.
6. Степнов М.Н. Статистические методы обработки результатов механических испытаний: Справочник. – М.: Машиностроение, 2005. - 399 с.
7. Дюк В. Обработка данных на ПК в примерах. - СПб: Питер, 1997. - 240 с.
Вопросы и задачи к главе 4.
1. Как определяется ошибка среднего значения «механической» выборки?
2. Почему связаны ошибка выборочного наблюдения и объём выборки?
3. Что называют «выбросом»?
4. Какие критерии обнаружения «выбросов» Вы знаете?
5. Установите по критерию Райта наличие «выбросов» в выборке размеров (мм): 5,25; 5,26; 5,26; 5,26; 5,27; 5,27; 5,31.
Вопросы и задачи к главе 5.
1. Чем характеризуется стандартное нормальное распределение?
2. Назовите основные непрерывные распределения.
3. Назовите основные дискретные распределения.
4. Объясните сущность распределения Пирсона
5. Объясните сущность распределения Фишера
6. Объясните сущность распределения Стьюдента.
7. Чем отличаются функции НОРМОБР от, СТЪЮДРАСПОБР от СТЪЮДРАСП, ФИШЕРОБР от ФИШЕР и. т. д.
8. Опишите методику расчёта вероятности попадания размера детали в интервал допустимых значений с помощью функции НОРМРАСП, если известны параметры рассеяния.
5.6 Дополнительная литература к главе 4.
1. ГОСТ Р 50779.52-95. Статистические методы. Приемочный контроль качества по альтернативному признаку. Общие требования. - Введ. 1996-07-01. - М.: Изд-во стандартов, 1996. - 229 с.
2. ГОСТ Р 50779.53-98. Статистические методы. Приемочный контроль качества по количественному признаку для нормального закона распределения. Часть I. Стандартное отклонение известно. - Введ. 1999-01-01. - М.: Госстандарт России, 1998. - 18 с.
3. ГОСТ Р 50779.51-95. Статистические методы. Непрерывный приемочный контроль качества по альтернативному признаку. - Введ. впервые 01.07.1996. - М.: Изд-во стандартов, 1996. - 16 с.
4. ГОСТ Р 50779.70-99 (ИСО 2859.0-95). Статистические методы. Процедуры выборочного контроля по альтернативному признаку. Часть 0. Введение в систему выборочного контроля по альтернативному признаку на основе приемлемого уровня качества AQL. - Введ. 2000-07-01. - М.: Изд-во стандартов, 2000. - 53 с.
5. Шелест, Вячеслав Дмитриевич Начала вычислительной математики: введение в численный эксперимент / Житомирский, Михаил Сергеевич; С.-Петербургский гос. политехнич. ун-т. - СПб. : Изд-во Политехнического ун-та, 2005. - 201 с.
Пример использования функции MS EXCEL ДОВЕРИТ для расчёта доверительный интервала единичного и среднего.
Функция ДОВЕРИТ(рис. 6.1) по данным выборкиопределяет половину доверительного интервала для единичного значения xi генеральной совокупности (аргумент «Размер» = 1, см. рис. 6.1) или для среднего значения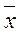 
выборки (аргумент «Размер» равен объёму выборки n).
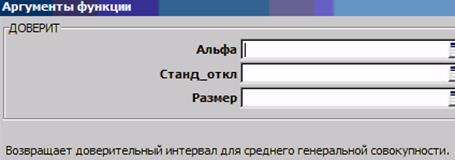
Рис. 6.1. Аргументы функции ДОВЕРИТ
Выборочное среднее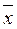 
является серединой этого интервала, следовательно, доверительный интервал определяется как ( ± 
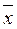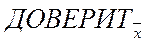), где 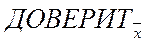- результат расчёта с использованием функции ДОВЕРИТ. Например, если 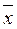- выборочное среднее значение размера детали, то математическое ожидание генеральной совокупности размера этой детали μ0 (или единичное значение 
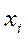, см ниже) с заданной доверительной вероятностью (например, 95%, что соответствует уровню значимости α = 0,05) принадлежит интервалу ( 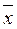± 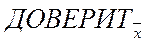). Для любого математического ожидания μ0, не принадлежащего интервалу ( 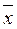± 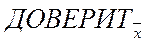), вероятность того, что выборочное среднее 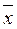(или единичное значение 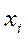, см ниже) отличается от μ0 более чем на 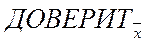, меньше заданной доверительной вероятности (< 95%). Аналогичным образом вероятность того, что единичное значение 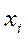, отличается от μ0 более чем на 
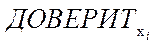, меньше заданной доверительной вероятности (< 95%).
Величина ДОВЕРИТ зависит от величины СКО, заданной вероятности и размера выборки. Зависимость от n определяется выражением:
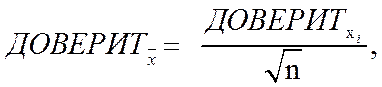(6.3)
где 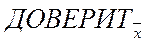- результат расчёта функции ДОВЕРИТ для выборки размером n, 
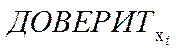- результат расчёта функции ДОВЕРИТ для единичного значения.
То есть результат расчёта функции ДОВЕРИТ для единичного значения 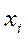в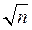 
раз больше, чем ДОВЕРИТ для среднего значения выборки, т.к. таким же образом различаются их стандартные отклонения, см. формулу 3.7.
Пример 1.Выполнить расчёт величины доверительного интервала единичного и выборочного среднего размера детали с использованием функции MS EXCEL ДОВЕРИТ по данным примера предыдущего параграфа: σ = 0,03 мм, g = 0,95 (α =0,05), n = 36.
Подставляем в аргументы функции ДОВЕРИТ (см. рис. 6.1) σ, α и «размер»
Получаем для единичного (размер n = 1) и среднего (размер n = 36) следующие значения величины доверительного интервала:
| «размер» | ||
| «ДОВЕРИТ» | 0,058799 | 0,0098 |
Таким образом, результаты соответствуют результатам, полученным традиционным табличным способом.
Пример 2. Индикаторным прибором размер одной детали контролировался 5 раз со следующими результатами (в мм): 5,587, 5,588, 5,589, 5,588, 5,586.
Определить точность контроля с надёжностью 95 % и с надёжностью 99 % для случаев, когда в инструкции к контрольному прибору регламентируется:
- одноразовый контроль в каждой точке,
- девятиразовый контроль в каждой точке с последующим усреднением.
Решение.Точность контроля, то есть величина доверительного интервала равна удвоенному результату расчёта с использованием функции ДОВЕРИТ. Предварительно по результатам контроля определяется выборочное СКО (функция СТАНДОТКЛОН). Полученное значение или ссылку на ячейку, содержащую его, следует вставить в качестве аргумента «Станд_откл» функции ДОВЕРИТ (см. рис. 6.1). В качестве аргумента «Альфа» следует вставить уровень значимости α, соответствующий требуемой надёжности (0,01 для надёжности 99 %, или 0,05 для надёжности 95 %). В качестве аргумента «Размер» следует вставить не объём n выборки, используемой для определения выборочного СКО (5), а регламентируемое количество параллельных контрольных операций (1 или 9). Результаты различных вариантов расчёта представлены в табл. 6.1.
Таблица 6.1. Результаты расчётов точности контрольного прибора
| Стандартное отклонение | ≈ 0,00102 | |
| Уровень значимости α (требуемая надёжность в %) | 0,05 (95 %) | 0,01 (99 %) |
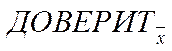 | ≈ 0,000745 | ≈ 0,000979 |
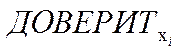 | ≈ 0,0022347 | ≈ 0,002937 |
| Точность девятиразового контроля | ≈ 0,00149 | ≈ 0,001958 |
| Точность одноразового контроля | ≈ 0,00447 | ≈ 0,005874 |
Сравнение результатов параллельных расчётов, приведённых в табл. 6.1, показывает, что для девятиразового контроля величина ДОВЕРИТ в 3 раза меньше и, соответственно, точность девятиразового контроля в 3 раза выше, чем для случая одноразового контроля. То есть результаты подтверждают формулу (6.3).
С другой стороны, сравнение результатов, полученных для различных уровней значимости α (требуемая надёжность в %) показывает, что для α = 0,01 величина ДОВЕРИТ в ≈ 1,314 раза больше, чем для α = 0,05. Это объясняется соответствующим увеличением интегральной функции попадания в доверительный интервал с уменьшением уровня значимости (увеличением заданной вероятности), см. § 6.1.
Статистических гипотез
Теоретические представления
Требуется проверить нулевую гипотезу о равенстве пар значений в выборках Xi и Yi. Проверка статистической гипотезы проводится следующим образом: вычисляют разности выборочных значений Xi и Yi. Полученный ряд разностей diсчитается выборкой объемом n. Рассчитывают характеристики новой выборки: среднее, число степеней свободы к = n - 1, выборочную дисперсию S2d и расчётное значение tP критерия Стьюдента для этого случая:
tP =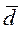 
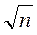/ Sd. (7.11)
Критическая область строится для нулевой гипотезы о равенстве средних в зависимости от вида конкурирующей гипотезы, при этом рассматриваются три вида конкурирующей гипотезы.
Первая конкурирующая гипотеза: «средние не равны».
В этом случае строят двустороннюю критическую область. По формуле вычисляют опытное значение критерия, определяют число степеней свободы. По таблице критических точек распределения Стьюдента, по заданному уровню значимости α и числу степеней свободы kопределяют критическую точку tKp.<