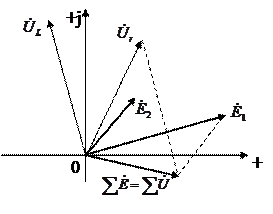Законы Кирхгофа для цепей синусоидального тока
Математическая формулировка двух законов Кирхгофа для цепей синусоидального тока зависит от выбранного представления синусоидальных величин. Будем далее пользоваться для аналитического представления синусоидальных величин тригонометрическими функциями и соответствующими им комплексными значениями. При тригонометрической форме представления законы Кирхгофа определяют зависимость между мгновенными значениями соответствующих синусоидальных величин. При втором виде представления законы Кирхгофа определяют зависимость между комплексными значениями соответствующих синусоидальных величин.
Первый закон Кирхгофа.
По первому закону Кирхгофа алгебраическая сумма токов в любом узле электрической цепи в каждый момент времени равна нулю. Для цепей синусоидального тока это означает, что в ветвях, сходящихся в любом узле, алгебраическая сумма мгновенных значений токов равна нулю:
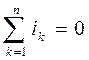
или
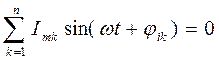 ,
,
где n – число ветвей, сходящихся в узле.
Принято соглашение о том, что все синусоидальные токи, положительные направления которых выбраны к узлу (от узла), записываются со знаком плюс (минус).

Положим
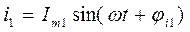
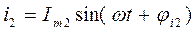
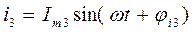 .
.
Тогда по первому закону Кирхгофа
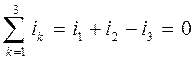
для любого момента времени.
Чтобы получить математическую формулировку первого закона Кирхгофа в комплексной форме, представим все синусоидальные токи соответствующими им комплексными значениями. Тогда первый закон Кирхгофа запишется следующим образом:
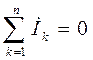 ,
,
то есть алгебраическая сумма комплексных значений тока всех ветвей, сходящихся в каком-либо узле электрической цепи, равна нулю.
Векторная диаграмма токов:
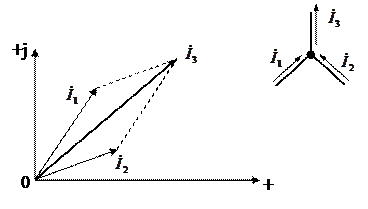
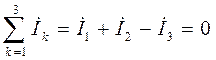 .
.
Второй закон Кирхгофа.
По второму закону Кирхгофа алгебраическая сумма напряжений на резистивных, индуктивных и емкостных элементах (пассивные элементы) в любом контуре электрической цепи в каждый момент времени равна алгебраической сумме ЭДС этого контура. В цепях синусоидального тока значения напряжений на пассивных элементах любого контура непрерывно изменяются, но, тем не менее, алгебраические суммы мгновенных значений напряжений и ЭДС одинаковы:
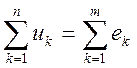
или
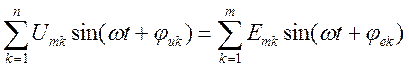 ,
,
где n – количество пассивных элементов в контуре, m – количество источников ЭДС в контуре. Будем считать, что все синусоидальные напряжения uk и ЭДС ek, для которых положительные направления совпадают с произвольно выбранным направлением обхода контура, записываются со знаком плюс и в противном случае со знаком минус.
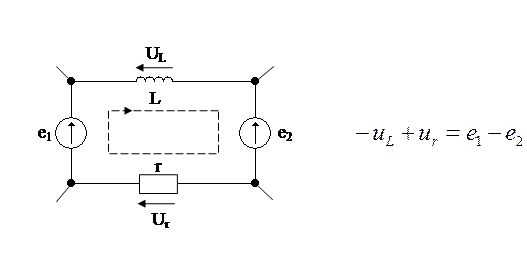
Чтобы получить математическую формулировку второго закона Кирхгофа в комплексной форме, представим все синусоидальные напряжения и ЭДС соответствующими комплексными значениями.
Второй закон Кирхгофа в комплексной форме записывается:
 ,
,
то есть алгебраическая сумма комплексных значений напряжений на всех пассивных элементах какого-либо контура электрической цепи равна алгебраической сумме комплексных значений всех ЭДС этого контура. В этом случае комплексные значения напряжений и ЭДС положительны, если совпадают с произвольно выбранным направлением обхода контура.
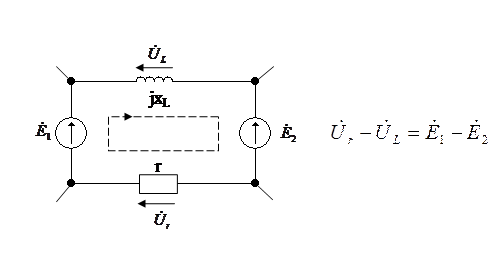
Векторная диаграмма ЭДС и напряжений: