Визуализация результатов экстраполяции
Результаты экстраполяции и оценки погрешности удобно представлять на графике в виде зависимости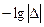 
(десятичного логарифма относительной погрешности) от логарифма n (числа отрезков разбиения) или h (шага сетки при равномерном разбиении). При этом каждая составляющая (степенная функция) представлялась бы на таком графике отрезком прямой. Значение ординаты соответствует числу верных знаков. В реальном случае отличие кривой, соответствующей результату определенной экстраполяции, от прямой свидетельствует о влиянии других составляющих погрешности. Надежные оценки получаются при достаточно большом расстоянии между точками кривых.
Оценку погрешности D можно проводить по правилу Рунге (сравнивать приближенное значение с экстраполированным, которое получено для этого приближенного значения). Можно также все приближенные значения сравнивать с одним числом, которое считается наиболее точным. Второй способ является более надежным при наличии нерегулярных составляющих (см. рис. П3.1, П3.2). Оценки погрешности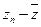 
зависят от выбора эталона 
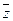, с которым сравниваются приближенные значения. Чтобы оценить эту зависимость и связать ее с величиной размытости оценки, рассмотрим разность
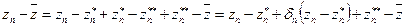. (15)
Величину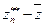 
можно сравнить с 
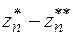и выразить в виде
,
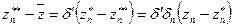где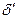 
– некоторый коэффициент. Абсолютная величина 
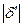связана с неопределенностью выбора эталона. Из практических соображений можно утверждать, что эта величина меньше 1, иначе это существенно исказило бы верхние кривые. Порядок этой величины определяется по графику разностью ординат между точками на двух верхних линиях. Поскольку для ее определения можно использовать не 3 значения, а относительное положение кривых, влияние случайных факторов на оценку погрешности и размытости существенно уменьшается.
Согласно (15)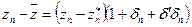 
.
Таким образом, величина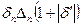 
имеет тот же смысл, что и значение 
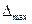, а если 
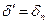, то эти определения совпадают с точностью до третьего члена геометрической прогрессии.
Численная фильтрация применялась для обработки результатов, полученных различными численными методами. В качестве примера на рис. 11,а приведены результаты вычисления второй производной по симметричной разностной формуле второго порядка, на рис. 11,б результаты численного интегрирования методом правых прямоугольников. В результате анализа можно утверждать, что вычисленные значения интегралов имеют 1-5 точных десятичных знаков, результат первой экстраполяции 3-10 знаков при относительной размытости менее 0.1.
Ограничение на уровне 14-15 знака объясняется погрешностью округления (применялись числа с двойной точностью). При этом следует отметить увеличение погрешности округления при численном дифференцировании с ростом n. При численном интегрировании этот рост погрешности округления менее заметен.
Аналогично выглядят результаты обработки численных данных, полученных при решении дифференциальных уравнений (обыкновенных и с частными производными).