Неустойчивая АСР и их переходные процессы.

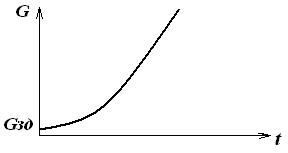
(г)- апериодический расходящийся

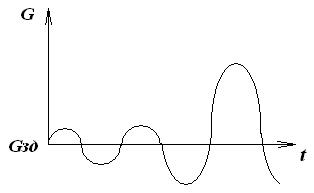
(д)- колебательный расходящийся

Параметры колебательного переходного процесса:

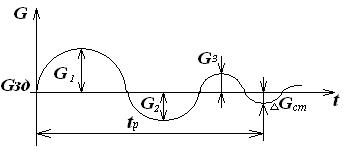tр – время переходного процесса или время регулирования – это интервал времени от начала воздействия до момента достижения параметром стабильного значения.

∆G₁ – максимальное динамическое отклонение или динамическая ошибка регулирования – это есть максимальное отклонение регулируемого параметра от заданного значения.

∆G_СТ – статическая ошибка регулирования – это остаточное отклонение параметра от G_ЗД в установившемся режиме, когда процесс регулирования закончен.

∆G_СТ дают П- и ПД-регуляторы.

Величина перерегулирования: .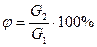

Наиболее приемлемым является процесс с 20% перерегулированием. Желаемый вид переходного процесса достигают путем установки соответствующей настройки регулятора: D, Т_i и Т_Д.

33. Импульсная характеристика системы. Методы экспериментального снятия импульсных характеристик. Виды импульсных характеристик.

Импульсная характеристика (ИХ, англ. impulse response, импульсный отклик) является важнейшей характеристикой линейных систем во временной области. Для систем непрерывного времени - это реакция (выходной сигнал) системы на входной сигнал в виде дельта – функции δ(t) при нулевых начальных условиях. Будем обозначать её как h(t) – отклик (выход) системы в момент t на входной сигнал в виде δ – функции. Нулевые начальные условия означает: выходной сигнал y(t) и все его производные в момент t = 0 имеют нулевые значения.

Экспериментальное определение ИХ заключается в определении отклика системы на достаточно узкий входной импульс x(t) единичной площади. При этом определяется приближенная импульсная характеристика.

Для нестационарных линейных систем импульсная характеристика зависит от момента воздействия дельта – функции τ ко входу системы, т.е. в этом случае она является функцией двух переменных, h(t, τ) - выход системы в момент t на δ – функцию 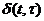, приложенную ко входу в момент τ.

Если линейная непрерывная система является стационарной (ЛНСС), или иначе инвариантной во времени (англ. linear time invariant system – LTI system), то её импульсная характеристика h(t) не зависит от сдвига во времени, т.е. является только функцией t.

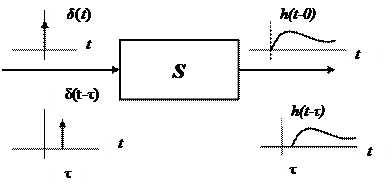
Импульсной характеристикой линейной дискретной стационарной системы (ЛДСС) называется её реакция на входной сигнал в виде единичного импульса δ[n] при нулевых начальных условиях. Будем обозначать её через h[n].

Виды импульсных характеристик

Простейшей импульсной характеристикой системы является дельта-функция (рисунок 4.11). В этом случае, любой входной импульс приводит к появлению на выходе такой системы точно такого же импульса. Т.е., все сигналы проходят через систему без изменений. Сверткой сигнала с дельта-функцией является сам сигнал.

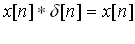(4.5)

Дельта-функция обладает свойством тождественности (identity) для операции свертки (как 0 для сложения 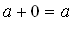, или 1 для умножения 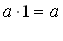). На первый взгляд такая импульсная характеристика для системы неинтересна. Но это не так! Такие системы используются для хранения данных, передачи данных или для измерений. С точки зрения ЦОС – такая система передает данные без изменений и разрушений.

Следующая импульсная характеристика является небольшой модификацией дельта-функции. Если дельта-функцию увеличить или уменьшить по амплитуде, то соответствующая ей система будет усилителем или аттенюатором, соответственно. В математическом виде, усилитель – еслиК больше единицы, аттенюатор – если К меньше единицы:

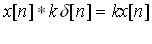(4.6)

Еще один вид импульсной характеристики представляет собой сдвинутую (shift) дельта-функцию. В результате, такая система будет формировать соответствующий сдвиг между входным и выходным сигналами. Данная система будет обладать свойством задержки (advance)сигнала, в зависимости от направления сдвига.

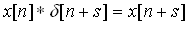(4.7)

Реализация системы с такой импульсной характеристикой не требует выполнения алгоритма свертки. Воспользуемся альтернативной функцией: суммой взвешенных отсчетов входного сигнала. Тогда, первый дифференциал может быть вычислен как:

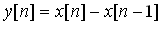, (4.8)

т.е. каждый отсчет выходного сигнала равен разности соседних отсчетов входного сигнала. Это один из способов определения дискретной производной. Другой способ определения первого дифференциала – использование симметрии отсчетов:

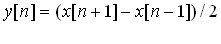(4.9)

Применяя такой же подход, любой отсчет для скользящей суммы может быть определен суммированием всех точек входного сигнала, расположенных левее текущего отсчета. Для получения значения отсчета 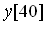необходимо просуммировать отсчеты с 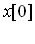по 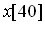. В другом виде, скользящую сумму можно записать так:

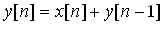(4.10)

Выражения такого типа называются рекурсивными уравнениями или дифференциальными уравнениями. Основная идея заключается в том, что реализация этих выражения абсолютно точно соответствует выполнению операции свертка с импульсной характеристикой системы, показанной на рисунке 4.12.

34. Понятие импульсной характеристики. Расчет импульсной характеристики системы. Классификация систем по виду импульсной характеристики.

Импульсная характеристика (ИХ, англ. impulse response, импульсный отклик) является важнейшей характеристикой линейных систем во временной области. Для систем непрерывного времени - это реакция (выходной сигнал) системы на входной сигнал в виде дельта – функции δ(t) при нулевых начальных условиях. Будем обозначать её как h(t) – отклик (выход) системы в момент t на входной сигнал в виде δ – функции. Нулевые начальные условия означает: выходной сигнал y(t) и все его производные в момент t = 0 имеют нулевые значения.

Наиболее просто определить передаточную функцию для последовательности идеализированных d-импульсов В этом случае одиночный “тестирующий” импульс представляет собой d-функцию d(t), а реакция системы на его воздействие — это импульсная характеристика цепи h_d(t). Поэтому передаточная функция импульсной системы представляет z-изображение последовательности значений этой характеристики, взятых через интервалы времени Т:

.

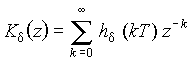После суммирования ряда функция K_d(z) приводится к дробно-рациональной функции переменной z.

Для RC-цепи имеем h_d(t) = e^–t/t (t = RC) и

.

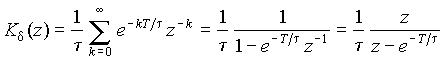Для более сложных цепей импульсная характеристика выражается суммой экспонент

,

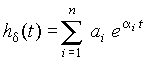где a_i — корни характеристического уравнения цепи (полюсы передаточной функции K(s); п — число корней; a_i — вычеты в полюсах.

Применение z-преобразования к каждому из слагаемых суммы приводит к результату

.

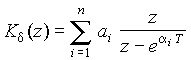При действии последовательности прямоугольных импульсов длительностью T_и для определения передаточной функции цепи используем полученное ранее выражение дискретной импульсной характеристики. Так, для простейших интегрирующих цепей имеем 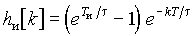. Получим z-изображение этой последовательности:

,

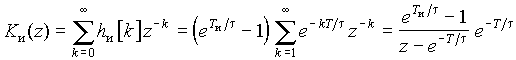что совпадает с результатом, полученным ранее для этой же цепи при помощи разностных уравнений [отношение U₂(z)/U₁(z) из формулы ].

Из приведенных соотношений следует, что передаточная функция K_и(z) зависит не только от структуры и элементов цепи, но и от формы воздействующих на цепь импульсов и интервала их следования T.

Как и в системах непрерывного времени, где коэффициенты дифференциального уравнения, связывающего входную и выходную величины, определяются коэффициентами полиномов числителя и знаменателя передаточной функции K(s), коэффициенты полиномов числителя и знаменателя K(z) представляют коэффициенты разностного уравнения, связывающего входную и выходную величины. Так, передаточная функция 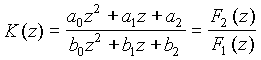соответствует разностному уравнению

.

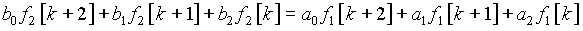Простейшей импульсной характеристикой системы является дельта-функция (рисунок 4.11). В этом случае, любой входной импульс приводит к появлению на выходе такой системы точно такого же импульса. Т.е., все сигналы проходят через систему без изменений. Сверткой сигнала с дельта-функцией является сам сигнал.

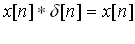(4.5)

Дельта-функция обладает свойством тождественности (identity) для операции свертки (как 0 для сложения 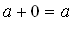, или 1 для умножения 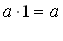). На первый взгляд такая импульсная характеристика для системы неинтересна. Но это не так! Такие системы используются для хранения данных, передачи данных или для измерений. С точки зрения ЦОС – такая система передает данные без изменений и разрушений.

Следующая импульсная характеристика является небольшой модификацией дельта-функции. Если дельта-функцию увеличить или уменьшить по амплитуде, то соответствующая ей система будет усилителем или аттенюатором, соответственно. В математическом виде, усилитель – еслиК больше единицы, аттенюатор – если К меньше единицы:

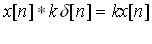(4.6)

Еще один вид импульсной характеристики представляет собой сдвинутую (shift) дельта-функцию. В результате, такая система будет формировать соответствующий сдвиг между входным и выходным сигналами. Данная система будет обладать свойством задержки (advance)сигнала, в зависимости от направления сдвига.

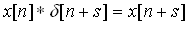(4.7)

Реализация системы с такой импульсной характеристикой не требует выполнения алгоритма свертки. Воспользуемся альтернативной функцией: суммой взвешенных отсчетов входного сигнала. Тогда, первый дифференциал может быть вычислен как:

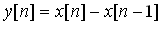, (4.8)

т.е. каждый отсчет выходного сигнала равен разности соседних отсчетов входного сигнала. Это один из способов определения дискретной производной. Другой способ определения первого дифференциала – использование симметрии отсчетов:

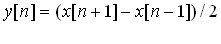(4.9)

Применяя такой же подход, любой отсчет для скользящей суммы может быть определен суммированием всех точек входного сигнала, расположенных левее текущего отсчета. Для получения значения отсчета 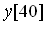необходимо просуммировать отсчеты с 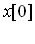по 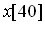. В другом виде, скользящую сумму можно записать так:

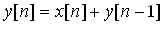(4.10)

Выражения такого типа называются рекурсивными уравнениями или дифференциальными уравнениями. Основная идея заключается в том, что реализация этих выражения абсолютно точно соответствует выполнению операции свертка с импульсной характеристикой системы, показанной на рисунке 4.12.

35. Понятие устойчивости систем. Теория устойчивости и ее значение в методах расчета систем управления.

Линейная система называетсяустойчивой, если при выведении ее внешними воздействиями из состояния равновесия (покоя) она возвращается в него после прекращения внешних воздействий. Если после прекращения внешнего воздействия система не возвращается к состоянию равновесия, то она является неустойчивой. Для нормального функционирования системы управления необходимо, чтобы она была устойчивой, так как в противном случае в ней возникают большие ошибки.

Определение устойчивости обычно проводят на начальном этапе создания системы управления. Это объясняется двумя причинами. Во-первых, анализ устойчивости довольно прост. Во-вторых, неустойчивые системы могут быть скорректированы, т.е. преобразованы в устойчивые с помощью добавления специальных корректирующих звеньев.

Теория устойчивости — техническая и физико-математическая дисциплина, изучающая закономерности поведения систем под действием внешних воздействий.

В аналитическом аспекте является разделом теории дифференциальных уравнений. В прикладном аспекте наибольшее развитие получила теория устойчивости механических систем, поскольку именно механика, как старейшая наука, впервые столкнулась с проблемами устойчивости. Эйлер впервые строго поставил и решил задачу устойчивости состояния равновесия механический системы — стержня, сжатого сжимающей силой (эластика Эйлера).

36. Характеристическое уравнение системы, метод его получения. Параметры системы, определяемые по характеристическому уравнению.

арактеристическое уравнение составляется для цепи после коммутации. Оно может быть получено следующими способами:

• непосредственно на основе дифференциального уравнения вида (2) (см. лекцию №24), т.е. путем исключения из системы уравнений, описывающих электромагнитное состояние цепи на основании первого и второго законов Кирхгофа, всех неизвестных величин, кроме одной, относительно которой и записывается уравнение (2);
• путем использования выражения для входного сопротивления цепи на синусоидальном токе;
• на основе выражения главного определителя.

Согласно первому способу в предыдущей лекции было получено дифференциальное уравнение относительно напряжения 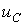на конденсаторе для последовательной R-L-C-цепи, на базе которого записывается характеристическое уравнение.

Следует отметить, что, поскольку линейная цепь охвачена единым переходным процессом, корни характеристического уравнения являются общими для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение. Поэтому по первому способу составления характеристического уравнения в качестве переменной, относительно которой оно записывается, может быть выбрана любая.

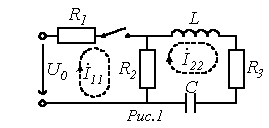Применение второго и третьего способов составления характеристического уравнения рассмотрим на примере цепи рис. 1.

Составление характеристического уравнения по методу входного сопротивления заключается в следующем:

записывается входное сопротивление цепи на переменном токе;

jw заменяется на оператор р;

полученное выражение 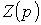приравнивается к нулю.

Уравнение

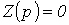
совпадает с характеристическим.

Следует подчеркнуть, что входное сопротивление может быть записано относительно места разрыва любой ветви схемы. При этом активный двухполюсник заменяется пассивным по аналогии с методом эквивалентного генератора. Данный способ составления характеристического уравнения предполагает отсутствие в схеме магнитосвязанных ветвей; при наличии таковых необходимо осуществить их предварительное развязывание.

Для цепи на рис. 1 относительно зажимов источника

.

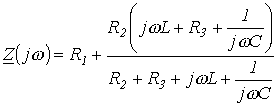Заменив jw на р и приравняв полученное выражение к нулю, запишем

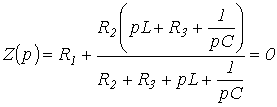
или

.

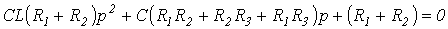(1)

При составлении характеристического уравнения на основе выражения главного определителя число алгебраических уравнений, на базе которых он записывается, равно числу неизвестных свободных составляющих токов. Алгебраизация исходной системы интегро-дифференциальных уравнений, составленных, например, на основании законов Кирхгофа или по методу контурных токов, осуществляется заменой символов дифференцирования и интегрирования соответственно на умножение и деление на оператор р. Характеристическое уравнение получается путем приравнивания записанного определителя к нулю. Поскольку выражение для главного определителя не зависит от правых частей системы неоднородных уравнений, его составление можно производить на основе системы уравнений, записанных для полных токов.

Для цепи на рис. 1 алгебраизованная система уравнений на основе метода контурных токов имеет вид

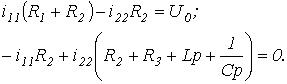
Отсюда выражение для главного определителя этой системы

.

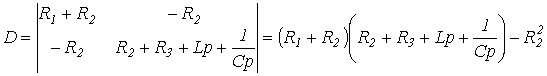Приравняв D к нулю, получим результат, аналогичный (1).

37. Теорема Ляпунова и ее применение. Виды переходных процессов в системах с различной степенью устойчивости.