Общий вид линейной системы автоматического управления

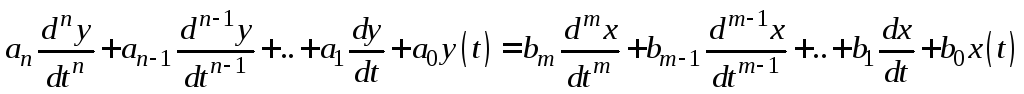
В реальных условиях большинство элементов автоматической системы являются не линейными (имеют статические характеристики)

Линеаризация– Процесс преобразования нелинейных уравнений в линейные

1. Графически:

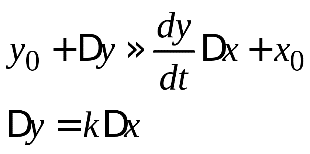
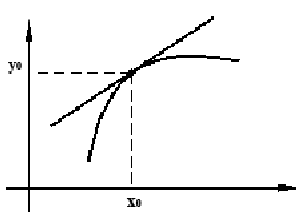
1. Аналитически:

С помощью разложения в ряд Тейлора в районе рабочей точки и исключая члены высших порядков малости

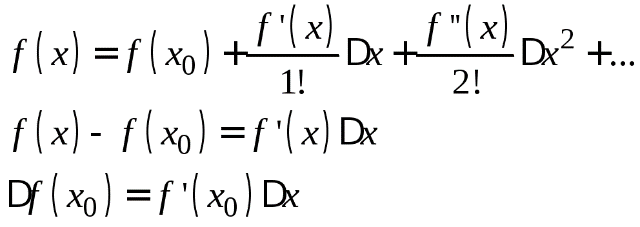
17. Принципы математического моделирования динамических процессов во временной области с помощью дифференциальных уравнений.

Математическое моделирование.

Классификация математических моделей.

Математические модели могут быть детерменированными и стохастическими.

Детерменированные модели- это модели, в которых установлено взаимно-однозначное соответствие между переменными описывающими объект или явления.

Такой подход основан на знании механизма функционирования объектов. Часто моделируемый объект сложен и расшифровка его механизма может оказаться очень трудоемкой и длинной во времени. В этом случае поступают следующим образом: на оригинале проводят эксперименты, обрабатывают полученные результаты и, не вникая в механизм и теорию моделируемого объекта с помощью методов математической статистики и теории вероятности, устанавливают связи между переменными, описывающими объект. В этом случае получают стахостическую модель. В стахостической модели связь между переменными носит случайный характер, иногда это бывает принципиально. Воздействие огромного количества факторов, их сочетание приводит к случайному набору переменных описывающих объект или явление. По характеру режимов модель бывают статистическими и динамическими.

Статистическая модель включает описание связей между основными переменными моделируемого объекта в установившемся режиме без учета изменения параметров во времени.

В динамической модели описываются связи между основными переменными моделируемого объекта при переходе от одного режима к другому.

Модели бывают дискретными и непрерывными, а также смешанного типа. В непрерывных переменные принимают значения из некоторого промежутка, в дискретных переменные принимают изолированные значения.

Линейные модели- все функции и отношения, описывающие модель линейно зависят от переменных и не линейные в противном случае.

Математическое моделирование.

Требования, предъявляемые к моделям.

1. Универсальность - характеризует полноту отображения моделью изучаемых свойств реального объекта.

2. Адекватность - способность отражать нужные свойства объекта с погрешностью не выше заданной.

3. Точность - оценивается степенью совпадения значений характеристик реального объекта и значения этих характеристик полученных с помощью моделей.

4. Экономичность - определяется затратами ресурсов ЭВМ памяти и времени на ее реализацию и эксплуатацию.

18. Функциональная схема и принцип действия замкнутой системы автоматического регулирования частоты вращения двигателя.

Функциональная схема предназначена для разъяснения процессов, происходящих в отдельных функциональных цепях изделия или изделии в целом. Для сложного изделия разрабатывается несколько функциональных схем, поясняющих происходящие процессы при различных предусмотренных режимах работы. Количество функциональных схем, разрабатываемых на изделие, степень их детализации и объем помещаемых сведений определяется разработчиком с учетом особенностей изделия.

На схеме изображают функциональные части изделия (элементы, устройства, функциональные группы) и связи межу ними. Графическое построение схемы должно наглядно отражать последовательность функциональных процессов, происходящих в изделии. Действительное расположение в изделии элементов и устройств может не учитываться.

Функциональные части и связи между ними изображают в виде условных графических обозначений, установленных в соответствующих стандартах на условные графические обозначения этих групп и элементов. В этом случае действуют правила выполнения принципиальных схем. Отдельные функциональные части на схеме допускается изображать в виде прямоугольников. В этом случае эти части схемы следует выполнять по правилам структурных схем.

По функциональной схеме указывают:

- для функциональных групп - обозначение, присвоенное ей на принципиальной схеме, или наименование (если функциональная группа изображена в виде условного графического обозначения, то ее наименование не указывают),

- для каждого устройства и элемента, изображенного условными графическими обозначениями - буквенно-цифровое позиционное обозначение, присвоенное на принципиальной схеме, его тип,

- для каждого устройства, изображенного прямоугольником - позиционное обозначение, присвоенное ему на принципиальной схеме, его наименование и тип или обозначение документа, на основании которого это устройство применено. Обозначение документа указывают и для устройства, изображенного в виде условного графического обозначения. Наименования, типы и обозначения функциональных частей, изображенных прямоугольниками, рекомендуется вписывать внутрь прямоугольников. Сокращенные или условные наименования должны быть пояснены на поле схемы.

Замкнутые системы автоматического управления (САУ) отличаются от разомкнутых применяемой аппаратурой и полнотой автоматизации. В разомкнутой САУ задающее устройство (включающая, регулирующая аппаратура) не получает информацию о фактическом режиме работы электроустановки (приводного электродвигателя, рабочей машины).

В замкнутой САУ информация передается на элементы управления, что сопровождается подачей соответствующих командных сигналов. Цепочка, передающая такую информацию, замыкает контур управления, образуя замкнутую САУ, или САУ с обратными связями.

Различие между замкнутой и разомкнутой САУ можно пояснить па примере регулирования скорости электродвигателя в системе генератор — двигатель (Г—Д). В разомкнутой САУ (рис. 1,а) заданная скорость электродвигателя устанавливается вручную потенциометром П. Контроль скорости осуществляется визуально по тахометру, получающему питание от тахогенератора ТГ. Всякое отклонение скорости от заданной оператор устраняет воздействием на движок потенциометра.

В замкнутой САУ (рис. 1,б) якорь тахогенератора ТГ включен в цепь обмотки возбуждения генератора ОВГ, создавая замкнутую систему, или систему с обратной связью (в данном случае с обратной связью по скорости).

Рис. 1. Схема регулирования электродвигателя в системе Г- М: а - разомкнутая САУ, б - замкнутая САУ

Ток, создаваемый тахогенератором (Iтг) в замкнутой цепи, направлен навстречу току потенциометра (Iп), и в цепи действует результирующий ток, равный геометрической разности этих токов. Движком потенциометра оператор устанавливает такое значение результирующего тока в обмотке возбуждения ОВГ, при котором обеспечивается соответствующая скорость электродвигателя. На этом роль оператора заканчивается. В дальнейшем система автоматически с определенной точностью поддерживает заданный режим работы электропривода.

Допустим, что в результате наброса нагрузки скорость электродвигателя уменьшилась по сравнению с заданной. Уменьшение скорости сопровождается соответствующим уменьшением скорости тахогенератора и напряжения на его зажимах. Это в свою очередь вызовет уменьшение тока Iтг в цепи обратной связи и в определенном положении движка потенциометра — увеличение результирующего тока в обмотке возбуждения генератора. Соответственно возрастут напряжение на генераторе и скорость электродвигателя.

Процесс увеличения скорости и напряжения будет продолжаться до тех пор, пока ток в цепи обратной связи не достигнет установленного значения, а скорость электродвигателя — заданной величины.

При анализе систем автоматического управления широко используют функциональные схемы. На рис. 2 показана функциональная схема САУ, которая включает следующие элементы:

1 — задающее устройство, которое задает режим работы, подает командный, начальный импульс или сигнал,

2 — элемент сравнения. В него входит сигнал Х1 от задающего устройства, сигнал Х0, определяющий норму или уровень контролируемой величины. С учетом сигнала от элемента 9-й главной обратной связи элемент 2 сравнивает поступившие сигналы и посылает дальше скорректированный сигнал Х2,

3 — преобразующий элемент, поступающий в него сигнал оп преобразует в другую форму, более удобную для дальнейшей передачи. Например, сигнал Х2 был дан в форме гидравлического (пневматического, механического) давления. Элемент 3 преобразовал его в электрический ток. Так как подобного рода преобразование может требовать дополнительной энергии, то элемент 3 связан с источником энергии ПЭ,

4 — суммирующий элемент, в него поступают два сигнала: Х3 и Х8 от корректирующего элемента (элемента памяти) 8. Эти сигналы суммируются элементом 4 в направляются в следующий элемент,

5 — элемент усиления, входящий сигнал Х1 может быть слабым и для последующей передачи должен быть усилен. Это делается элементом 5, который связан с источником энергии ПЭ,

6 — исполнительный элемент, выполняет полученный сигнал (электродвигатель, электромагнитное реле, серводвигатель),

7 — регулируемый объект, или рабочая машина.

Рис. 2. Функциональная схема САУ

19. Принцип действия и математическое моделирование посредством дифференциальных уравнений замкнутой системы автоматического регулирования частоты вращения двигателя.

(??????????????????????????????????????????????????????)

20. Общий вид дифференциального уравнения звена системы. Праметры, входящие в дифференциальное уравнения звена. Преобразования Лапласа. Цели преобразования уравнения к виду Лапласа.

Основной характеристикой любой динамической системы, наиболее полно отражающей ее свойства, является дифференциальное уравнение.

Процессы, описывающие линейную САУ, соответственно, будут описываться линейным дифференциальным уравнением.

Общий метод составления дифференциального уравнения системы: для каждого звена автоматической системы в соответствии с его теорией составляют дифф.ур. связывающее его выходную величину с входной. В результате получают систему уравнений, количество которых равно числу звеньев. Входные и выходные величины – основные, остальные промежуточные, которые из системы исключаются при ее решении.

Уравнение линейного динамического звена имеет следующий общий вид:

Так как все функции и их производные стоят в первой степени, для такого дифференциального уравнения выполняется принцип суперпозиции, следовательно, такая система линейна.

Дифференциальные уравнения сложны, для упрощения описания САУ и анализа их функционирования применяется преобразование Лапласа. Делаем мы это, чтобы получить передаточную функцию САУ

Передаточная функция системы – это отношение изображения по Лапласу выходной управляемой величины к изображению по Лапласу задающего воздействия.

Подвергнем уравнение (1) преобразованию Лапласа, считая начальные условия нулевыми и заменяя оригиналы сигналов их изображениями по Лапласу

.

Используя теоремы преобразования Лапласа линейности и дифференцирования, получим операторное уравнение, связывающие изображения входного и выходного сигналов

(2)

Преобразуем уравнение (2) к следующему виду

(3)

Получим из (3) отношение изображений выходного и входного сигналов

(4)

Отношение (4) не зависит от изображений сигналов, определяется только параметрами самого динамического звена ( ), имеет вид дробно-рациональной функции.

Отношение изображений выходного и входного сигналов называют передаточной функцией динамического звена

.

Уравнение вида

,

называют характеристическим уравнением динамического звена, так как знаменатель передаточной функции – это характеристический полином дифференциального уравнения, описывающего динамическое звено.

Преобразование Лапласа находит широкое применение во многих областях математики (операционное исчисление), физики и техники:

· Решение систем дифференциальных и интегральных уравнений — с помощью преобразования Лапласа легко переходить от сложных понятий математического анализа к простым алгебраическим соотношениям.

· Расчёт передаточных функций динамических систем, таких, к примеру, как аналоговые фильтры.

· Расчёт выходных сигналов динамических систем в теории управления и обработке сигналов — так как выходной сигнал линейной стационарной системы равен свёртке её импульсной характеристики с входным сигналом, преобразование Лапласа позволяет заменить эту операцию на простое умножение.

· Расчёт электрических схем. Производится путём решения дифференциальных уравнений, описывающих схему операторным методом.

· Решение нестационарных задач математической физики

21. Передаточная функция системы. Пример вывода передаточной функции.