Тема 1.1. Некоторые сведения из теории матричной алгебры
МАТЕМАТИЧЕСКИЕ ЗАДАЧИ
ЭЛЕКТРОЭНЕРГЕТИКИ
Конспект лекций дпя студентов,
обучающихся по направлению “Электроэнергетика”
Иркутск 2009
Раздел 1. Применение матричной алгебры и теории графов
В электроэнергетике
Тема 1.1. Некоторые сведения из теории матричной алгебры
Классификация матриц
Система m n чисел, действительных или комплексных, расположенных в прямоугольной таблице из m строк и n столбцов называется матрицей
 .
.
где aij – элементы матрицы;
i = 1, 2, 3,…., m – номера строк;
m – число строк в матрице;
j = 1, 2, 3,…., n – номера столбцов;
n – число столбцов.
Для матрицы часто используется сокращенная запись  , где m·n – размерность матрицы.
, где m·n – размерность матрицы.
Если m = n (m ≠ 1, n ≠ 1), то матрица называется квадратной.
Если m ≠ n (m ≠ 1, n ≠ 1), то матрица называется прямоугольной.
Если m = n = 1, то матрица - скаляр.
Если m = 1, а n ≠ 1, то матрица называется вектор-строкой
 .
.
Если n = 1, а m ≠ 1, то матрица называется вектор-столбцом
 .
.
Матрица нулевого порядка смысла не имеет.
Квадратная матрица, у которой диагональные элементы не равны нулю, а все недиагональные элементы равны нулю, называются диагональной


Диагональная матрица, у которой все ненулевые элементы равны единице, называется единичной и обозначается Е
 .
.
Матрица, все элементы которой равны нулю, называется нулевой и обозначается через О
 .
.
Определитель
Определитель (или детерминант) является важной числовой характеристикой квадратной матрицы, обозначается через  или det A и вычисляется по известным правилам. Классический способ вычисления
или det A и вычисляется по известным правилам. Классический способ вычисления  (первый способ)
(первый способ)
 ,
,
где q1,q2,…,qn – произвольная перестановка вторых индексов;
П – число беспорядков в перестановке вторых индексов.
Число слагаемых произведений равно числу возможных перестановок вторых индексов, т.е. равно n!, где n - порядок квадратной матрицы.
Пример:

| Возможные перестановки вторых индексов | Число беспорядков | |
 | 1) 1 2 3 | П=0 |
 | 2) 1 3 2 | П=1 |
 | 3) 2 1 3 | П=1 |
 | 4) 2 3 1 | П=2 |
 | 5) 3 1 2 | П=2 |
 | 6) 3 2 1 | П=3 |


Число слагаемых произведений при вычислении Δ возрастает стремительно с увеличением n:
n = 2 2! = 2
n = 3 3! = 6
n = 4 4! = 24
n = 5 5! = 120
n = 6 6! = 720
Вычислять Δ классическим способом сложно и поэтому применяют другие способы.
Вычисление Δ для матрицы второго порядка (n = 2).

Два частных способа вычисления Δ для матриц только третьего порядка (n = 3).
 | Слагаемые произведения со знаком +  |
 | Слагаемые произведения со знаком -  |

| 2) |  |
Указанные схемы вычисления Δ для матриц второго и третьего порядков основаны на использовании геометрического расположения элементов в матрицах, что неприменимо для матриц более высокого порядка.
Миноры и алгебраические дополнения
Минором Мij элемента аij матрицы А, называется определитель матрицы (n-1)-ого порядка, полученной из матрицы А путем вычеркивания i-й строки и j-го столбца.
Алгебраическим дополнением называется минор, вычисляемый по формуле:
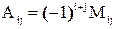 .
.
Действия с матрицами
1. Сумма и разность матриц.
Могут складываться и вычитаться матрицы только одинакового типа.
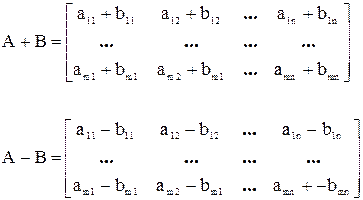
Из сложения матриц вытекают следующие свойства:
1) А+(В+С)=(А+В)+С;
2) А+В=В+А;
3) А+0=А.
2. Умножение матрицы на скаляр.
Отсюда: 1) 1А=А; 2) 0А=0;
3) α (β А) = (αβ) А; 4) αА + βА = (α+β) А;
5) α (А+В) = αА + αА;
3. Умножение матриц А * В = С.
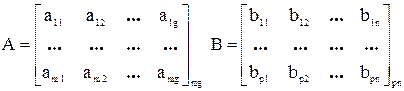
Перемножать матрицы можно только в том случае, если число столбцов первой матрицы равно числу строк второй матрицы, т.е. g=p, а число строк первой матрицы и число столбцов второй матрицы могут быть любые, т.е. m≠n. Результатом будет матрица С размерностью mn, элементы которой
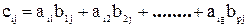
Для вычисления элемента, стоящего в i-й строке и j-м столбце произведения двух матриц, нужно элементы i-ой строки первой матрицы умножить на соответствующие элементы j-го столбца второй матрицы и полученные произведения сложить.
Свойства:
1) А(ВС)=(АВ)С;
2) α(АВ)=(αА)В;
3) (А+В)=АС+АВ.
4)
Запомнить, что в общем случае 4) АВ≠ВА.
Пример:
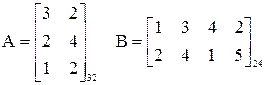
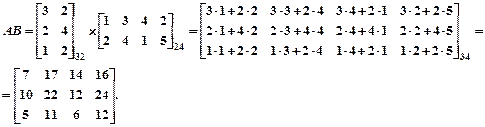
В тех частных случаях, когда АВ=ВА, матрицы А и В называются перестановочными. Например, единичная матрица Е перестановочна с любой матрицей А того же порядка.
АЕ=ЕА=А.
Единичная матрица Е играет роль единицы при умножении.
Транспонированная матрица
Если в матрице 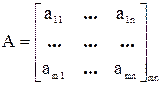 строки и столбцы поменять местами, то получим транспонированную матрицу.
строки и столбцы поменять местами, то получим транспонированную матрицу.
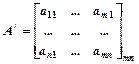
Свойства:
1) дважды транспонированная матрица равна исходной
А = (А ) = А;
2) (А+В) =А + В ;
3) (АВ) =В А , т.е. (АВ) ≠ А В ;
4) Если А =А, то матрица А - симметричная
(аij = aji)
Обратная матрица
Обратной матрицей по отношению к данной квадратной, называется матрица, которая, будучи умноженной как справа, так и слева на данную матрицу, дает единичную матрицу. Обозначим для матрица А обратную ей матрицу через А-1.
АА-1=А-1А=Е.
Нахождение обратной матрицы для данной называется обращением данной матрицы.
Квадратная матрица называется неособенной, если ее определитель не равен нулю, в противном случае матрица называется особенной или сингулярной. Обратная матрица имеет только у неособенной матрицы.
Пусть имеем матричное равенство
АС=В.
Умножим правую и левую часть равенства на обратную матрицу А-1
А-1АС= А-1В.
Поскольку известно, что А-1А=Е, то
ЕС= А-1В.
И поскольку известно, что ЕС=С, то
С= А-1В.
То есть, мы равенство АС=В преобразовали в равенство С= А-1В, выразив матрицу С.
Если бы у нас были простые алгебраические числа а, b и с, то аналогичные преобразования были бы следующие: 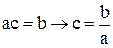 .
.
Сравнив преобразования для алгебраических чисел и матриц видим, что обращение матрицы соответствует действию деления. Поэтому понятна необходимость в обратной матрице, в ее вычислениях.
Метод обратной матрицы
Дана система линейных уравнений
А∙Х=В.
Умножим правую и левую части системы на обратную матрицу А-1
А-1∙А∙Х= А-1∙В
Так как А-1∙А=Е, то Е∙Х= А-1∙В ЕХ=Х
Так как ЕХ=Х то, Х= А-1∙В.
Таким образом данный метод заключается в нахождении обратной матрицы коэффициентов А-1 и ее умножении на вектор свободных членов В. Нахождение обратной матрицы А-1 при порядке n>4 требует много времени, поэтому метод обратной матрицы редко употребляется.
Метод Крамера
Известно, что
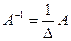 .
.
Отсюда
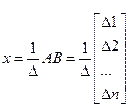 ,
,
где 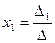 ,
, 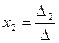 , …,
, …, 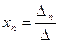
где 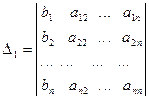
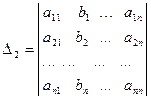
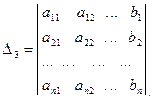
Итак, метод Крамера заключается в вычислении (n+1)-го определителя (∆1, ∆2, ∆3, …, ∆n) для матриц n-го порядка. Если число велико, то вычисление определителей является трудоемкой задачей.
Наиболее распространенным способом решения системы линейных уравнений является метод последовательного исключения неизвестных или метод Гаусса.
Метод Гаусса
Рассмотрим на простейшем примере известный со школы способ исключения неизвестных при решении систем уравнений. Пусть дана система:
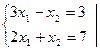
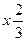
Умножим первое уравнение на такой коэффициент 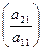 , чтобы в обоих уравнениях коэффициент при х1 стал бы одинаковым
, чтобы в обоих уравнениях коэффициент при х1 стал бы одинаковым
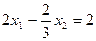
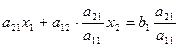
Теперь вычтем его из второго уравнения, т.е.
-2х1+х2=7
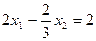
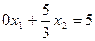
Мы выполнили операцию исключения неизвестной х1 из второго уравнения. Запишем систему уравнения после этого исключения в следующем виде. Первое уравнение записываем в исходном виде.
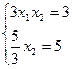
Второе уравнение содержит лишь одно неизвестное, которое легко вычисляется х2=3. Подставив полученное значение х2 в первое уравнение, можем вычислить и первое неизвестное х1.
Проведенные действия и составляют сущность метода Гаусса. Рассмотрим преобразования по методу Гаусса для системы уравнений n-го порядка.
| а11х1+ а12х2+ … +а1nхn=b1 |
| 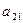 | 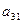 | 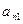 | |||
| а21х1+ а22х2+ … +а2nхn=b2 | 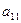 | 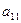 | 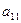 | ||||
| а31х1+ а32х2+ … +а3nхn=b3 | |||||||
| … … … … | |||||||
| аn1х1+ аn2х2+ … +аnnхn=bn |
Вычтем из второго уравнения первое, умноженное на 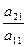 .
.
При этом во втором уравнении будет уничтожен коэффициент при х1.
Затем из третьего уравнения также вычтем первое, умноженное на 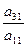 .
.
Проделав аналогичные преобразования с остальными уравнениями системы, превратим в нуль все коэффициенты первого столбца, кроме элемента а11. Получим следующую систему:
| а11х1+ а12х2+ а13х3+… +а1nхn=b1 | 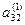 | … | 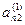 |
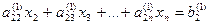 | 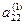 | 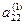 | |
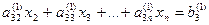 | |||
| … … … … | |||
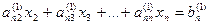 |
Затем при помощи второго уравнения преображенной системы исключим из третьего, четвертого и т.д. уравнений коэффициенты второго столбца лежащие ниже 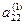
а11х1+ а12х2+ а13х3+… +а1nхn=b1
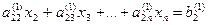
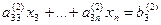
… … …
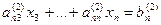
Последовательно продолжая этот процесс, исключим из системы все коэффициенты, лежащие ниже главной диагонали. В результате получим треугольную систему уравнений.
а11х1+ а12х2+ а13х3+… +а1nхn=b1
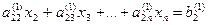
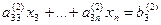
… … …
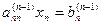
Процесс получения треугольной системы называется “прямым ходом” по методу Гаусса. Треугольная система легко решается “обратным ходом”. Из последнего уравнения определяется последнее неизвестное 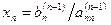 . Затем из предпоследнего уравнения постановкой найденного значения хn определяется хn-1. После решения системы уравнений методом Гаусса необходимо делать проверку, подставляя в исходные уравнения найденные значения переменных хi (i= 1, …, n).
. Затем из предпоследнего уравнения постановкой найденного значения хn определяется хn-1. После решения системы уравнений методом Гаусса необходимо делать проверку, подставляя в исходные уравнения найденные значения переменных хi (i= 1, …, n).
При решении системы линейных уравнений методом Гаусса все вычисления можно поместить в следующую таблицу. Рассмотрим таблицу на примере решения системы уравнений третьего порядка.
| № шага преобразований | х х1 | х х2 | х х3 | ||
| 1) |  а11 а11 | а12 | а13 | b1 |  : а11 : а11 |
| а21 | а22 | а23 | b2 | ||
| а31 | а32 | а33 | b3 | ||
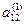 | 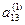 | 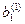 | |||
| 1 2) |  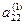 |  |  |  : : 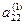 | |
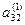 | 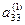 | 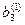 | |||
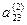 | 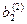 | ||||
| 2 3) | 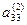 | 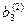 |  : : 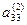 | ||
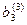 |
Уравнения 1), 2) и 3) составляют искомую треугольную матрицу после “прямого хода”. Число шагов преобразований в “прямом ходе” методом Гаусса равно n-1.
Коэффициенты а11, 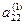 ,
, 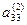 - называются “ведущими” элементами.
- называются “ведущими” элементами.
При “обратном ходе” можно использовать строки таблицы, содержащие единицы, т.е. вспомогательные уравнения. Имеем 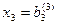 далее
далее
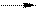
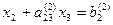
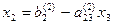
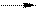
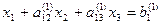
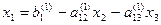
ПРИМЕР:
| № шага | х1 | х2 | х3 | B | ||
| : 4 | ||||||
| 0,25 | 0,5 | х 2 | х 1 | |||
| 7,5 | ||||||
| 1,75 | 3,5 | |||||
| 0,4 | 3,2 | х 1,75 | ||||
| 2,8 | 8,4 | |||||
 Треугольная система
Треугольная система
 4 х1+х2+2х3=12
4 х1+х2+2х3=12
 7,5 х2+3х3=24
7,5 х2+3х3=24
 2,8 х3=8,4
2,8 х3=8,4
или
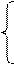 х1+0,25х2+0,5х3=3
х1+0,25х2+0,5х3=3
х2+0,4х3=3,2
х3=3
Обратный ход
х2=3,2-0,4∙3=2
х1=3-0,25∙2-0,5∙3=1
Вычисление определителя методом Гаусса
(третий способ, без вывода)
Определитель матицы А равен произведению всех “ведущих” элементов при преобразовании ее по методу Гаусса.
Для вычисления определителя матрицы А выполняется только “прямой” ход методом Гаусса, причем столбец свободных членов В становится излишним.
ПРИМЕР: дана матрица
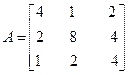 detА=4∙7,5∙2,8=84
detА=4∙7,5∙2,8=84
 Вычисление обратной матрицы методом Гаусса
Вычисление обратной матрицы методом Гаусса
А∙А-1 = Е
Матрицы А и Е известны, требуется определить А-1. Обозначим столбцы матрицы А-1 через х1, х2, …, хn т.е.
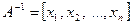
Столбцы для матрицы Е обозначим через Е1, Е2, …, Еn
Тогда можем записать n систем уравнений
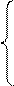 Ах1=Е1
Ах1=Е1
Ах2=Е2
Ахn=Еn
Развернем первое матричное уравнение Ах1=Е1
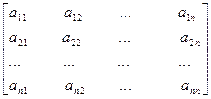 х
х 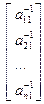 =
= 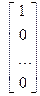
Другие матричные уравнения аналогичны.
Следовательно, для получения обратной матрицы А-1 достаточно выполнить n решений методом Гаусса систем линейных уравнений с разными правыми частями - y столбцами матрицы Е.
Полученные решения х1, х2, …, хn будут столбцами искомой обратной матрицы А-1.
Трангуляции матрицы
Квадратную матрицу А можно представить как произведение двух треугольных матриц А=LW, где
L – нижняя треугольная матрица,
W – верхняя треугольная матрица.
Матрица W вычисляется при прямом ходе Гаусса
а11 а12 а13 … а1n
0 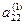
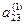 …
… 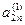
0 0 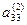 …
… 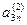
… … … … …
0 0 0 … 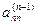
У матрицы L наоборот все элементы выше главной диагонали нулевые. Остальные элементы матрицы L вычисляются в результате деления элементов по столбцам, полученных при том же прямом ходе Гаусса, на ведущие элементы. Сначала вычисляются элементы первого столбца матрицы L делением на ведущий элемент а11, затем после первого шага “прямым ходом” метода Гаусса вычисляются элементы второго столбца, начиная с диагонального, делением на ведущий элемент а11 и т.д.
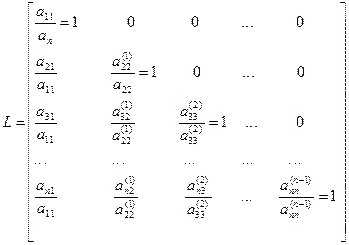
Требуется решить системы уравнений
Ах=В
Так как А=LW то LWх=В
Обозначим Wх=Z
Тогда вместо системы Ах=В можем записать ей эквивалентную
 LZ=В
LZ=В
Wx=Z (5)
Решение эквивалентной системы с треугольными матрицами L и W занимает гораздо меньше времени, чем решение исходной системы Ах=В. Это обстоятельство очень важно при необходимости решать систему уравнений многократно при одной и той же матрице А и разных векторах свободных членов В, что обычно имеет место при расчетах режимов работы электрических систем. Триангуляция же матрицы А проводится только один раз.
 То есть элементы матрицы А – это, как правило, параметры схемы замещения эл. системы, В – вектор узловых токов или мощностей. Часто ставится задача определения параметров большего числа режимов при изменении токов или мощностей потребителей в узлах при неизменной схеме замещения. Если триангуляция матрицы А осуществлена, то можно быстро пользуясь системой (5) посчитать необходимые режимы, меняя в этой системе вектор В. Для каждого режима сначала решается треугольная подсистема LZ=В относительно Z последовательной подстановкой в уравнения подсистемы найденных значений неизвестных из предыдущих уравнений, начиная с Z1
То есть элементы матрицы А – это, как правило, параметры схемы замещения эл. системы, В – вектор узловых токов или мощностей. Часто ставится задача определения параметров большего числа режимов при изменении токов или мощностей потребителей в узлах при неизменной схеме замещения. Если триангуляция матрицы А осуществлена, то можно быстро пользуясь системой (5) посчитать необходимые режимы, меняя в этой системе вектор В. Для каждого режима сначала решается треугольная подсистема LZ=В относительно Z последовательной подстановкой в уравнения подсистемы найденных значений неизвестных из предыдущих уравнений, начиная с Z1
Z1 =b1
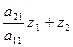 =b2
=b2
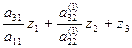 =b3
=b3
… … … … …
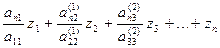 =bn
=bn
Значение Z1 уже известно из первого уравнения, Z2 определяется из второго уравнения подстановкой в него значения Z1 и т.д. Определяются все Z. Затем аналогично решается вторая треугольная подсистема Wx=Z путем обратной подстановки, начиная с хn (аналогично обратному ходу методом Гаусса).
Метод Жордана-Гаусса
Метод Жордана-Гаусса называют еще методом Гаусса без обратного хода. Сущность его состоит в том, что на втором шаге переменная исключается из всех уравнений, кроме второго, на третьем шаге исключается также из всех уравнений, кроме третьего и т.д. После шагов в каждом уравнении остается одна неизвестная, т.е. получим решение системы таким образом, исключение переменных по методу Жордана-Гаусса эквивалентно преобразованию матрицы коэффициентов в единичную. Рассмотрим таблицу вычислений по методу Жордана-Гауса.
| № шага преобразований | A | C | B | ||
| а11 | a12 | … | a1n | b1 | |
| а21 | a22 | … | a2n | b2 | |
| а31 | a32 | … | a3n | b3 | |
| … | … | … | … | … | |
| аn1 | an2 | … | ann | bn | |
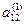 | … | 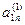 | 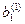 | ||
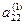 | … | 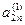 | 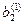 | ||
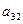 | … | 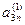 | 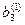 | ||
| … | … | … | … | … | |
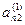 | … | 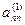 | 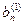 | ||
| … | … | … | … | … | … |
| n | … | 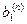 | |||
| … | 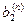 | ||||
| .. | .. | … | … | ||
| … | 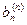 |
Нахождение обратной матрицы методом Жордана-Гаусса
 Рассмотрим вычислительную процедуру определителя А-1 на конкретном примере.
Рассмотрим вычислительную процедуру определителя А-1 на конкретном примере.
А∙А-1=Е
Пусть
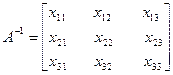
А х1 х2 х3 Е1 Е2 Е3
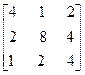 х
х 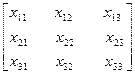 =
= 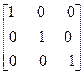
| № шага преобразования | х х1 | х х2 | х х3 | Е1 | Е2 | Е3 |
| 0,25 | 0,5 | 0,25 | ||||
| 7,5 | -0,5 | |||||
| 1,75 | 3,5 | -0,25 | ||||
| 0,4 | 0,2667 | -0,0333 | ||||
| 0,4 | -0,0667 | 0,1333 | ||||
| 2,8 | -0,1333 | -0,2333 | ||||
| 0,2857 | -0,1428 | |||||
| -0,0477 | 0,1666 | -0,1428 | ||||
| -0,0476 | -0,0833 | 0,357 |
Проверка:
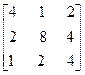 х
х 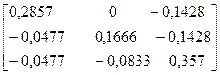 =
= 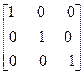
По такой же вычислительной схеме можно вычислять значения переменных х1, х2, х3, …, х при одной матрице коэффициента А и разных столбцах свободных членов В1, В2, В3, …, Вn.
Недостатки метода Гаусса (его недостатки и способы их устранения)
1. Если определитель матрицы А мал, то из-за ошибок округлений сильно снижается точность получения искомых корней.
2. Метод Гаусса требует, чтобы диагональные элементы в процессе исключения переменных не были равны нулю (т.к. строки делятся на них). Поэтому часть применяют метод Гаусса с выбором главного элемента, который заключается в следующем. При обращении в нуль элементов первого столбца из всей матрицы выбирается наибольший элемент и затем в нуль элементы второго столбца, рассматривается сокращенная матрица (путем вычеркивания в уже полученной системе первого уравнения) и в ней наибольший элемент переставляется на ее первое место и т.д.
3. Метод Гаусса требует большего объема памяти ЭВМ по сравнению с итерационными методами. Существуют различные приемы по сокращению занимаемой памяти ЭВМ при решении методом Гаусса электроэнергетических задач.
Например, необходимо решить систему
Yy ∙Uy=Iy
при использовании метода узловых напряжений.

Перенумерация
- Экономичность памяти
- Сокращение времени счета
| Y= | → | |||||||||||||||||||||||
| + | + | + | + | + | + | |||||||||||||||||||
| + | + | + | + | + | + | |||||||||||||||||||
| + | + | + | + | + | ||||||||||||||||||||
| + | + | + | + | + | + | |||||||||||||||||||
| + | + | + | + | |||||||||||||||||||||
| + | + | + | + | + | + | + | + | |||||||||||||||||
| + | + | + | + | + | + | + | ||||||||||||||||||
| + | + | + | + | + | + | |||||||||||||||||||
| + | + | + | + | + | + | + | + | |||||||||||||||||
| + | + | + | + | + |
(30 х 70)
Я=10 х 10=100 Я=52 (26)
В ряде случаев для нахождения корней системы линейных уравнений удобнее пользоваться приближенными итерационными методами (или методами последовательных приближений).
Метод простой итерации
Дана система линейных уравнений
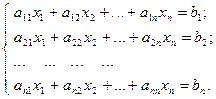
Предположим, что диагональные элементы аii, i = 1- n не равны 0. В любом случае строки и столбцы можно поменять местами так, чтобы диагональные элементы не были равны 0. Разделим каждую строку на ее диагональный элемент: первую строку на 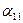 , вторую строку на
, вторую строку на 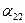 и т.д. Получим следующую систему
и т.д. Получим следующую систему
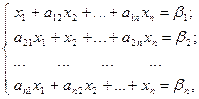
где 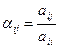 ;
; 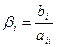 .
.
В матричном виде эту систему можно записать

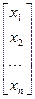 +
+ 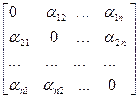 х
х 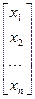 =
= 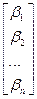 или
или 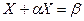 .
.
Отсюда 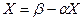 . (1)
. (1)
Выполненная выше операция называется приведением системы линейных уравнений к виду, удобному для итераций.
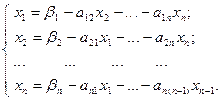
Зададим произвольное начальное значение всех неизвестных корней системы 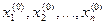 (в матричном виде Х = Х(0))и подставим это значение в правую часть системы уравнений (1).
(в матричном виде Х = Х(0))и подставим это значение в правую часть системы уравнений (1).
Вычислим 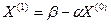 ,
,
где Х(0) – начальное (исходное) приближение к корням системы уравнений,
Х(1) - первое приближение к корням системы уравнений.
Затем процесс повторим, подставив найденные на первой итерации значения Х=Х(1) в правую часть системы уравнений и вычислим вторые приближения корней
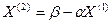 . И так далее.
. И так далее.
Итерационный процесс повторяем до тех пор, пока на какой-нибудь к-й итерации не выполнится условие
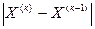 <ε,
<ε,
где ε – заданная точность определения корней системы.
Поскольку в вектор Х входит n неизвестных, то условие окончания итерационного процесса, должно быть выполнено для всех n корней.
Пример: дана система линейных уравнений
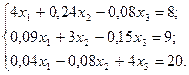
Приведем систему уравнений к виду, удобному для итерации
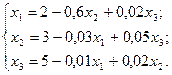
Зададим начальные приближения к корням равными нулю 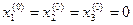 и точность расчета ε = 0,001.
и точность расчета ε = 0,001.
Начнем итерационный процесс вычисления корней.
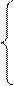 1 итерация
1 итерация 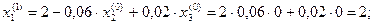
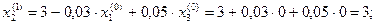
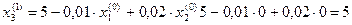
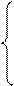 2 итерация
2 итерация 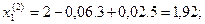
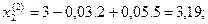
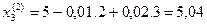
и т.д. до выполнения условий 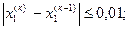
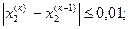
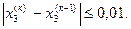
Вычисления сведем в таблицу
| № итерации (к) | 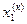 | 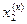 | 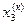 |
| 1,92 | 3,19 | 5,04 | |
Наши рекомендации
|
