В чем заключается тест Парка на гетероскедастичность?

Тестируем гетероскедастичность вида: Var(ε_i)=σ²Z²_i

3 шага:

1) получить остатки оцененной регрессии и сохранить их;

2) использовать их для оценки регрессии вида: ln(e²_i) =α₀+ α₁lnZi + ui

3) проверить на значимость 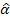₁ c помощью t-статистики. Отклонить нулевую гипотезу о наличии гетероскедастичности (если так оно и будет)

Каков алгоритм использования теста Голдфелда-Квандта?

Предполагаем, что σ_ui пропорционально значению X_i, σ_ui~N.

1) n наблюдений упорядочиваются по величине X, а затем оцениваются n’ первых и n’ последних наблюдений (средние наблюдения (n-2n’) отбрасываются. Дисперсия u в n’ последних наблюдениях должна быть больше, чем в n’ первых (гетероскедастичность), RSS1>RSS2- нулевая гипотеза

2) Рассчитываем RSS1/RSS2, которое имеет F-распределение с (n’-k) степенями свободы, где k- число параметров. Обычно n’=3/8n

3) сравниваем RSS1/RSS2 с F-критич.

Каково правило разделения на подвыборки для использования теста Голдфелда-Квандта?

n наблюдений упорядочиваются по величине X, а затем оцениваются n’ первых и n’ последних наблюдений (средние наблюдения (n-2n’) отбрасываются. Обычно n’=3/8n. Если в модели более одной объясняющей переменной, то наблюдения упорядочиваются по той из них, которая связана с σ_ui.

Какое распределение использует тест Голдфелда-Квандта? Как определяются

Соответствующие степени свободы?

F-распределение с (n’-k) степенями свободы, где k- число параметров в регрессионном уравнении, n’=3/8n.

Для чего используется поправка Уайта на гетероскедастичность при вычислении

Регрессии?

Корректировака Уайта добавляет в b характеристику устроенных ошибок (сумма произвед. ошибок), чтобы либо сгладить, либо устранить гетероскедастичность.

В чем состоит тест Уайта на гетероскедастичность?

Т.к. σ_ui² в i-м наблюдении неизвестна, то в качестве замещающей переменной используется квадрат отклонения для этого наблюдения.

1)Оценивается регрессия квадратов отклонений на объясняющие переменные модели, их квадраты и их попарные произведения (исключаются все повторяющиеся переменные). 2)nR²- тестовая статистика (R²-коэфф. детерминации).

3) nR² Vs c²_{критич.}(k-1), где k – число оцениваемых параметров. Проверяем верна ли нулевая гипотеза об отсутствии связи между дисперсией сл. члена и объясняющей переменной.

В чем различие теста Уайта при использовании перекрестных членов (cross-terms)

И без них?

Когда мы используем перекрестный член, то мы дополнительно оцениваем значимость совместного влияния двух факторов с точки зрения гетероскедастичности. ели без него, то одного фактора.

Тест Спирмена использует наиболее общие положения о зависимости дисперсий ошибок регрессии от значений регрессоров.

Тест Глейзера аналогичен тесту Уайта, но в качестве зависимой переменной выбирается абсолютная величина.

23. Методы смягчения гетероскедастичности.

Взвешенный метод наименьших квадратов компенсирует нарушение предпосылки гомоскедастичности случайного члена путем взвешивания коэффициентов. В случае оценки коэффициентов, если величина зависимой переменной соответствует большим колебаниям величины независимой переменной то их взвешивают в меньшей степени, а в тех случаях, когда небольшие колебания, то им (оценкам коэффициентов) придают большие веса.

Иногда взвешенный МНК иногда используется для подгонки, чтобы придать меньшие веса дальним значениям и резким выбросам

24. Суть мультиколлинеарности.

Наибольшие затруднения в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторных переменных, когда более чем два фактора связаны между собой линейной зависимостью.

Мультиколлинеарностью для линейной множественной регрессии называется наличие линейной зависимости между факторными переменными, включёнными в модель.

Мультиколлинеарность – нарушение одного из основных условий, лежащих в основе построения линейной модели множественной регрессии.

25. Последствия мультиколлинеарности.

Выделяются следующие последствия мультиколли­неарности:

1. Большие дисперсии (стандартные ошибки) оценок. Это затрудняет нахождение истинных значений определяемых величин и расширяет интервальные оценки, ухудшая их точность.

2. Уменьшаются 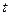-статистики коэффициентов, что может привести к неоправданному выводу о существенности влияния соответствующей объясняющей переменной на зависимую пе­ременную.

3. Оценки коэффициентов по МНК и их стандартные ошиб­ки становятся очень чувствительными к малейшим изменени­ям данных, т.е. они становятся неустойчивыми.

4. Затрудняется определение вклада каждой из объясняю­щих переменных в объясняемую уравнением регрессии диспер­сию зависимой переменной.

5. Возможно получение неверного знака у коэффициента регрессии.

26. Определение мультиколлинеарности.

Существует несколько признаков, по которым может быть установлено наличие мультиколлинеарности.

1. Совокупный коэффициент множественной детерминации (R2)достаточно вы­сок, но некоторые из коэффициентов регрессии статистически незначимы, то есть они имеют низ­киеt-статистики.

2. Парная корреляция между малозначимыми объясняющими переменными достаточно высока (в случае двух объясняющих переменных).

3. Высокие частные коэффициенты корреляции (в случае большего количества малозначимых объясняющих переменных).

27. Методы устранения мультиколлинеарности.

Рассмотрим ос­новные методы.

1. Исключение переменной(ых) из модели. Простейшим методом устранения мультиколлинеарности является ис­ключение из модели одной или ряда коррелированных переменных.

Однако в этой ситуации возможны ошибки специфика­ции. Например, при исследовании спроса на некоторое благо в качестве объясняющих переменных можно исполь­зовать цену данного блага и цены заменителей данного блага, которые зачастую коррелируют друг с другом.

Исключив из модели цены заменителей, скорее всего, будет допущена ошибка спецификации. Вследствие это­го можно получить смещенные оценки и сделать необос­нованные выводы. Поэтому в прикладных эконометрических моделях желательно не исключать объясняющие переменные до тех пор, пока коллинеарность не станет серьезной проблемой.

2. Получение дополнительных данных или новой вы­борки. Поскольку мультиколлинеарность напрямую за­висит от выборки, то, возможно, при другой выборке мультиколлинеарности не будет, либо она не будет столь серьезной.

Иногда для уменьшения мультиколлинеарности дос­таточно увеличить объем выборки. Увеличение количе­ства данных сокращает дисперсии коэффициентов рег­рессии и, тем самым, увеличивает их статистическую зна­чимость.

Однако получение новой выборки или расширение ста­рой не всегда возможно или связано с серьезными издер­жками.

3. Изменение спецификации модели. В ряде случаев про­блема мультиколлинеарности может быть решена путем изменения спецификации модели: либо изменяется фор­ма модели, либо добавляются объясняющие переменные, не учтенные в первоначальной модели, но существенно влияющие на зависимую переменную.

Если данный метод имеет основания, то его использо­вание уменьшает сумму квадратов отклонений, тем самым, сокращая стандартную ошибку регрессии. Это приводит к уменьшению стандартных ошибок коэффициентов.

4. Использование предварительной информации о некото­рых параметрах. Иногда при построении модели множе­ственной регрессии можно воспользоваться предваритель­ной информацией, в частности известными значениями некоторых коэффициентов регрессии. Вполне вероятно, что значения коэффициентов, рассчитанные для каких-либо предварительных (обычно более простых) моделей либо для аналогичной модели по ранее полученной выборке, могут быть использованы для разрабатываемой в данный момент модели.

Ограниченность использования данного метода обус­ловлена тем, что, во-первых, получение предварительной информации зачастую затруднительно, а, во-вторых, ве­роятность того, что выделенный коэффициент регрессии будет одним и тем же для различных моделей, невысока.

Преобразование переменных. В ряде случаев миними­зировать либо вообще устранить проблему мультиколли­неарности можно с помощью преобразования переменных.

Например, пусть эмпирическое уравнение регрессии имеет следующий вид:

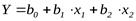(1)

При этом х₁ и х₂ – это коррелированные переменные.

В этой ситуации можно попытаться определять следующие рег­рессионные зависимости относительных величин:

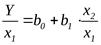(2)

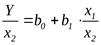(3)

Вполне вероятно, что в этих моделях проблема муль­тиколлинеарности будет отсутствовать. Возможны и дру­гие преобразования, близкие по своей сути к опи­санным выше. Например, если в уравнении рассматриваются взаимосвязи номинальных экономических показателей, то для снижения мультиколлинеарности можно попытать­ся перейти к реальным показателям и т.п.

28. Суть и причины автокорреляции.

Автокорреляция определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени или в пространстве. Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании перекрестных данных.

В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.

Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот.

Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:

1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.

2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.

3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом). Например, предложение сельскохозяйственной продукции реагирует на изменение цены с запаздыванием, равным периоду созревания урожая. Большая цена сельскохозяйственной продукции в прошедшем году вызовет скорее всего ее перепроизводство в текущем году, а следовательно, цена на нее снизится.

4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.

29. Последствия автокорреляции.

Последствия автокорреляции в определенной степени сходны с последствиями гетероскедастичности. Среди них при применении МНК обычно выделяют следующие.

1. МНК-оценки параметров, оставаясь несмещенными и линейными, перестают быть эффективными. Следовательно, они перестают обладать свойствами наилучших линейных несмещенных оценок.

2. Стандартные ошибки коэффициентов регрессии будут рассчитываться со смещением. Часто они являются заниженными, что влечет за собой увеличение t-статистик. Это может привести к признанию статистически значимыми объясняющих переменных, которые в действительности таковыми не являются. Смещенность возникает вследствие того, что выборочная остаточная дисперсия 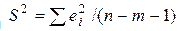(m – число объясняющих переменных модели), которая используется при вычислении указанных величин (см. формулы (2.18) и (2.19)), является смещенной. Во многих случаях она занижает истинное значение дисперсии возмущений s2.

Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F- статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при проверке качества оценок (параметров модели и самой модели в целом), могут быть ошибочными и приводить к неверным заключениям по построенной модели

30. Методы устранения автокорреляции.

Процедура Кохрейна-Оркатта. Процедура включает следующие этапы:

1. Применяя МНК к исходному уравнению регрессии, получают первоначальные оценки параметров и ;

2. Вычисляют остатки 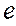и в качестве оценки 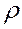используют коэффициент автокорреляции остатков первого порядка, ᴛ.ᴇ. полугают ;

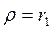3. Применяя МНК к преобразованному уравнению, получают новые оценки параметров 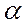и .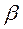

Процесс обычно заканчивается, когда очередное приближение 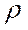мало отличается от предыдущего. Процедура Кохрейна-Оркатта реализована в большинстве эконометрических компьютерных программах.

Процедура Хильдрата-Лу. Эта процедура, также широко применяема в регрессионных пакетах, основана на тех же самых принципах, но использует другой алгоритм вычислений:

1. Преобразованное уравнение оценивают для каждого значения 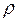из интервала (-1;1) с заданным шагом внутри его;

2. Выбирают значение 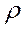, для которого сумма квадратов остатков в преобразованном уравнении минимальна, а коэффициенты регрессии определяются при оценивании преобразованного уравнения с использованием этого значения.

31. Обнаружение автокорреляции.

Метод рядов

Этот метод достаточно прост: последовательно определяются знаки отклонений 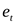,t=1,2…T. Например,

(-----)(+++++++)(---)(++++)(-),

Т.е. 5 «-», 7 «+», 3 «-», 4 «+», 1 «-» при 20 наблюдениях.

Ряд определяется как непрерывная последовательность одинаковых знаков. Количество знаков в ряду называется длиной ряда.

Визуальное распределение знаков свидетельствует о неслучайном характере связей между отклонениями. Если рядов слишком мало по сравнению с количеством наблюдений n, то вполне вероятна положительная автокорреляция. Если же рядов слишком много, то вероятна отрицательная автокорреляция .

Критерий Дарбина-Уотсона

32. Основные элементы временного ряда.

Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. В отечественной литературе используют два синонима этого термина: динамический ряд» и «ряд динамики», в англоязычной литературе – «time series».

Составными элементами временных рядов являются числовые значения показателя, называемые уровнями этих рядов, и моменты или интервалы, к которым относятся уровни.

Временные ряды, образованные показателями, характеризующими экономическое явление в определенные моменты времени, называют моментными; пример такого ряда представлен в табл. 9.1.

Табл. 9.1. Списочная численность рабочих предприятия

Дата	На 1 января	На 1 февраля	На 1 марта	На 1 апреля	На 1 мая	На 1 июня
Численность

Если временные ряды образуются путем агрегирования за определенный промежуток (интервал) времени, то такие ряды называются интервальными временными рядами; пример такого ряда приведен в табл. 9.2.

Табл. 9.2. Фонд заработной платы рабочих предприятия

Месяц	январь	февраль	март	апрель
Фонд заработной платы, тыс. руб.	37187,5	38270,0	39380,0	42535,0

Временные ряды могут быть образованы как из абсолютных значений экономических показателей (см. табл. 9.1 и 9.2), так и из средних (табл. 9.3) или относительных величин (табл. 9.4).

Табл. 9.3. Средняя месячная заработная плата рабочих предприятия

Месяц	январь	февраль	март	апрель
Средняя заработная плата, тыс. руб.

Табл. 9.4. Среднегодовой рост месячной заработной платы рабочих предприятия

Год
Среднегодовой рост заработной платы, %	125,3	119,7	115,4	117,5

33. Моделирование тенденции временного ряда.

Одним из наиболее распространённых способов моделирования тенденции временного ряда является построение аналитической функции характеризующей зависимость уровней ряда от времени или тренда. Способ называется аналитическим выравниванием временного ряда.

Поскольку зависимость от времени может принимать разные формы, для её формализации можно использовать различные виды функций.

Для построения трендов чаще всего применяются формулы:

1) Линейная зависимость

2) Гипербола

3) Экспоненциальный тренд

4) Тренд в форме степенной функции

5) Парабола 2го и более высоких порядков.

Параметры каждого из трендов можно определить обычным МНК (метод наименьших квадратов0 используя в качестве независимой время t=1,2,3….n , а в качестве зависимо переменной фактические уровни временного ряда Yt , для не линейных трендов предварительно проводят процедуру их линеаризации, известно несколько способов определения типа тенденции , к наиболее распространённым относятся качественный анализ изучаемого процесса построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики.

34. Моделирование сезонных и циклических колебаний.

Существует несколько подходов к анализу структуры времен­ных рядов, содержащих сезонные или циклические колебания. Моделирование циклических колебаний в целом осуществляется ана­логично моделированию сезонных колебаний, в связи с этим мы рассмотрим только методы моделирования последних Простейший подход - расчет значений сезонной компонен­ты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда. Общий вид аддитивной модели следующий:

Y= T+S+E (5.5)

Эта модель предполагает, что каждый уровень временного ря­да должна быть представлен как сумма трендовой (7), сезонной (S) и случайной (£) компонент. Общий вид мультипликативной мо­дели выглядит так:

Y=T*S*E (5.6)

Эта модель предполагает, что каждый уровень временного ряда должна быть представлен как произведение трендовой (7), сезонной (S) и случайной (Е) компонент. Выбор одной из двух моделœей осуществляется на базе анализа структуры сезонных колебаний. В случае если амплитуда колебаний приблизительно постоян­на, строят аддитивную модель временного ряда, в которой значе­ния сезонной компоненты предполагаются постоянными для различных циклов. В случае если амплитуда сезонных колебаний возрас­тает или уменьшается, строят мультипликативную модель вре­менного ряда, которая ставит уровни ряда в зависимость от зна­чений сезонной компоненты.

Построение аддитивной и мультипликативной моделœей сво­дится к расчету значений T, S и Е для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

1. Выравнивание исходного ряда методом скользящей средней.

2. Расчет значений сезонной компоненты S.

3. Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных (Т+Е) в аддитивной или (T*Е) вмультипликативной модели.

4. Аналитическое выравнивание уровней (T + Е) или (Т * Е) и расчет значений Т с использованием полученного уравнения тренда.

5. Расчет полученных по модели значений (T+S) или (T*S).

6. Расчет абсолютных и/или относительных ошибок.

В случае если полученные значения ошибок не содержат автокорреля­ции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок Е для анализа взаимосвязи исходного ряда и других временных рядов.

35. Общая характеристика моделей авторегрессии.

И/ИЛИ

Авторегрессионная (AR-) модель (англ. autoregressive model) — модель временных рядов, в которой значения временного ряда в данный момент линейно зависят от предыдущих значений этого же ряда. Авторегрессионный процесс порядка p (AR(p)-процесс) определяется следующим образом

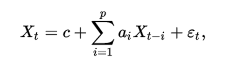
где {\displaystyle a_{1},\ldots ,a_{p}} — параметры модели (коэффициенты авторегрессии), {\displaystyle c} — постоянная (часто для упрощения предполагается равной нулю), а {\displaystyle \varepsilon _{t}} — белый шум.

Простейшим примером является авторегрессионный процесс первого порядка AR(1)-процесс:

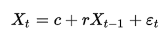
Для данного процесса коэффициент авторегрессии совпадает с коэффициентом автокорреляции первого порядка.

Другой простой процесс — процесс Юла — AR(2)-процесс:

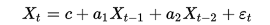
36. Оценка параметров моделей авторегрессии.

Рассмотрим модель авторегрессии первого порядка

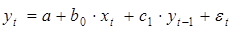. (5.8)

Одна из основных проблем при построении моделей авто­регрессии (при оценке параметров) связана с наличием корреляционной зависимости между переменной y_t-1 и остатками ε_t в уравнении регрес­сии, что приводит при применении обычного МНК к получению смещенной оценки параметра при переменной y_t-1.

Для преодоления этой проблемы обычно используется метод инструментальных переменных, согласно которому перемен­ная y_t–1 из правой части модели заменяется на новую переменную ŷ_t–1, которая, во-первых, должна тесно коррелировать с y_t–1, и, во-вторых, не коррелировать с ошибкой модели ε_t.

В качестве такой переменной можно взять регрессию переменной y_t–1 на переменную x_t–1, определяемую соотношением

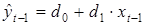, (5.9)

где константы d₁, d₂ являются коэффициентами уравнения регрессии

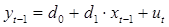, (5.10)

полученными с помощью обычного МНК.

В результате, для оценки параметров уравнения (5.8) используется уравнение

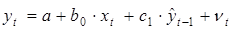, (5.11)

где значения переменной 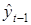рассчитаны по формуле (5.9).

Заметим, что функциональная связь между переменными 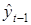и x_t–1 (5.9) приводит к появлению высо­кой корреляционной связи между переменными 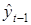и x_t. Для преодоления этой проблем в модель (5.8) и, соответственно, в модель (5.11) можно включить фактор времени в качест­ве независимой переменной. Модель при этом примет вид

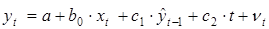. (5.12)

37. Общее понятие о системах уравнений, используемых в эконометрике.

Объектом статистического изучения в социальных науках являются сложные системы. Построение изолированных уравнений регрессии недостаточно для описания таких систем и объяснения механизма их функционирования.

Поэтому при моделировании экономических ситуаций часто необходимо построение систем уравнений, когда одни и те же переменные могут выступать и в роли объясняющих и в роли объясняемых. Так, если изучается модель спроса как отношение цен и количества потребляемых товаров, то одновременно для прогнозирования спроса необходима модель предложения товаров, в которой рассматривается также взаимосвязь между количеством и ценой предлагаемых благ. Это позволяет достичь равновесия между спросом и предложением.

Система уравнений в эконометрических исследованиях может быть построена по-разному.

Системы уравнений здесь могут быть построены по-разному.

Возможна система независимых уравнений,когда каждая зависимая переменная y рассматривается как функция одного и того же набора факторов x:

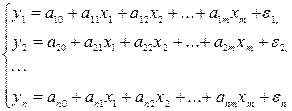(1)

Набор факторов x_j в каждом уравнении может варьироваться.

Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения его параметров используется МНК. По существу, каждое уравнение этой системы является уравнением регрессии.

Если зависимая переменная 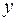одного уравнения выступает в виде фактора 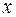в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений:

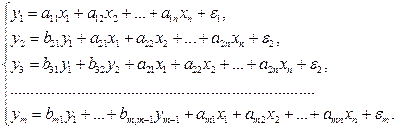(2)

В данной системе зависимая переменная 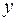включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором факторов 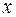. Каждое уравнение этой системы может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).

Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть системы:

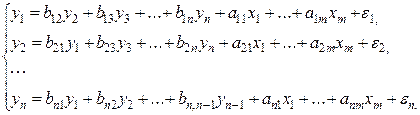(3)

Система взаимозависимых уравнений получила название системы совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений называется также структурной формой модели.

В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания.

38. Структурная и приведенная формы модели.

Система одновременных уравнений, т. е. структурная форма модели, обычно содержит эндогенные и экзогенные переменные.

Эндогенные переменные -это зависимые переменные, число которых равно числу уравнений в системе. Они обозначаются через y.

Экзогенные переменные -это предопределенные переменные, влияющие на эндогенные переменные, но независящие от них. Они обозначаются через x.

Простейшая структурная форма модели имеет вид:

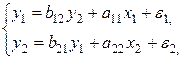
где 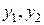– эндогенные переменные, 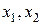– экзогенные.

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других – как экзогенные переменные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные. В качестве экзогенных переменных можно рассматривать значения эндогенных переменных за предшествующий период времени (лаговые переменные). Например, потребление текущего года y_t может зависеть также и от уровня потребления в предыдущем году y_t-1.

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.

Коэффициенты 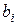при эндогенных и 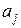– при экзогенных переменных называются структурными коэффициентами модели.Все переменные в модели могут быть выражены в отклонениях 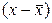и 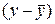от среднего уровня, и тогда свободный член в каждом уравнении отсутствует.

Использование МНК для оценивания структурных коэффициентов модели дает смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма преобразуется в приведенную.

Приведенная форма моделипредставляет собой систему линейных функций эндогенных переменных от экзогенных:

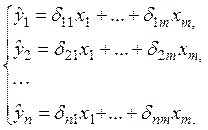(3)

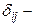коэффициенты приведенной формы модели.

По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений. Применяя МНК, можно оценить 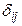, а затем оценить значения эндогенных переменных через экзогенные.

Приведенная форма позволяет выразить значения эндогенных переменных через экзогенные, однако аналитически уступает структурной форме модели, т. к. в ней отсутствуют оценки взаимосвязи между эндогенными переменными.

39. Проблема идентификации.

При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация–это единственность соответствия между приведенной и структурной формами модели.

Структурная модель (2) в полном виде, состоящая в каждом уравнении системы из n эндогенных и m экзогенных переменных, содержит 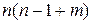параметров. Приведенная модель (3) в полном виде содержит nm параметров. Таким образом, в полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Поэтому 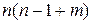параметров структурной модели не могут быть однозначно определены через nm параметров приведенной формы модели.

Чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что некоторые из структурных коэффициентов модели равны нулю. Тем самым уменьшится число структурных коэффициентов.

С позиции идентифицируемости структурные модели можно подразделить на три вида:

· идентифицируемые;

· неидентифицируемые;

· сверхидентифицируемые.

Модель идентифицируема,если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. число параметров структурной модели равно числу параметров приведенной формы модели.

Модель неидентифицируема,если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Модель (2) в полном виде всегда неидентифицируема.

Модель сверхидентифицируема,если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе приведенных коэффициентов можно получить два или более значений одного структурного коэффициента. Сверхидентифицируемая модель, в отличие от неидентифицируемой, практически решаема, но требует для этого специальных методов исчисления параметров.

Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо.Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.

Обозначим Н – число эндогенных переменных в i- ом уравнении системы, D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение. Тогда условие идентифицируемости уравнения может быть записано в виде следующего счетного правила:

D+1 = Н – уравнение идентифицируемо;

D+1 < Н – уравнение неидентифицируемо;

D+1 > Н – уравнение сверхидентифицируемо.

Это счетное правило отражает необходимое, но не достаточное условие идентификации. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.

40. Оценивание параметров структурной модели.

Наибольшее распространение получили следующие методы установления оценок коэффициентов структурной модели:

– косвенный метод наименьших квадратов (КМНК);

– двухшаговый метод наименьших квадратов (ДМНК).

КМНК используется в случае идентифицируемой структурной модели, а

для параметризации сверхидентифицируемых структурных моделœей используется ДМНК.

Косвенный МНК состоит в следующем:

1. Составляется приведенная форма модели.

2. Для каждого приведенного уравнения обычным МНК оцениваются приведенные коэффициенты.

3. С помощью алгебраических преобразований осуществляется переход от приведенной формы к уравнениям структурной формы модели. При этом приведенные коэффициенты трансформируются в численные оценки структурных параметров.

Смысл метода заложен в названии ʼʼкосвенный МНКʼʼ, ĸᴏᴛᴏᴩᴏᴇ подчеркивает, что структурные коэффициенты исходной модели находятся косвенно, ᴛ.ᴇ. через оценки приведенных коэффициентов.

Двухшаговый МНК состоит в следующем:

1. Составляется приведенная форма модели и с помощью обычного МНК определяются численные значения приведенных коэффициентов.

2. Выявляются эндогенные переменные из правой части структурного уравнения; находятся теоретические значения этих эндогенных переменных по соответствующим уравнениям приведенной формы модели.

3. Теоретические значения эндогенных переменных, стоящих в правых частях уравнений, подставляются вместо их фактических значен