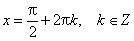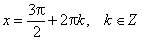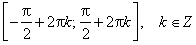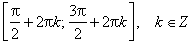Алгоритм разложения аналитической функции в степенной ряд

1. Найти производные от данной функции: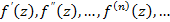

2. Вычислить значения производных в точке 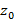; записать коэффициенты по формуле (3). Составить ряд по степеням 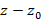с этими коэффициентами, который соответствует данной функции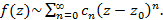

3. Найти область сходимости полученного ряда и записать разложение (1).

Если функция не имеет конечных особых точек, то ряд сходится к ней во всей плоскости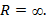

Утверждение

1. Функция, аналитическая в точке 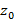, раскладывается в окрестности этой точки в степенной ряд.

2. На границе круга сходимости ряда есть хотя бы одна особая точка функции, т.е. радиус сходимости круга равен расстоянию от центра разложения 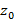до ближайшей особой точки функции.

3. Степенной ряд в круге сходимости является рядом Тейлора для своей суммы, т.е. коэффициенты ряда вычисляются по формулам (2), (3).

Логарифмическая функция комплексного переменного

Логарифмическая функция 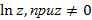определяется как обратная к показательной функции, причем:

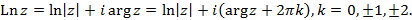
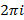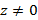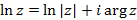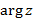Так как показательная функция- периодическая с периодом , то логарифмическая функция является многозначной. В каждой точке она принимает бесконечно много значений. Функция , где - главное значение аргумента, называется главным значением логарифмической функции. Итак: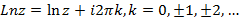

Известные правила о логарифме произведения и частного сохраняют свою силу и для многозначного логарифма, а именно при 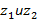, отличных от нуля верны формулы: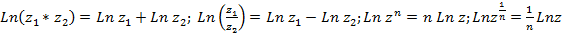

Методика изучения логарифмической функции в школьном курсе математики

Логарифмическая функция – новый математический объект для учащихся. К понятию логарифма учащихся подводят в процессе решения показательного уравнения a^x =b в том случае, если b нельзя представить в виде степени с основанием a. Наше уравнение в случае b>0 имеет единственный корень, который называют логарифмом b по основанию a и обозначают log_a b, т.е. a^logab =b. Одновременно с введением нового понятия учащиеся знакомятся с основным Логарифмическим тождеством. При работе с логарифмами применяются следующие их свойства, вытекающие из свойств показательной функции:

При любом 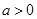( 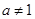) и любых положительных x и y, выполнены равенства:

1. log_a 1=0

2. log_a a=1

3. log_a xy= log_a x+ log_a y

4. log_a x/y= log_a x- log_a y

5. log_a x^p = plog_a x

При доказательстве используется основное логарифмическое тождество:

x=a^logax ; y=a^logay

Изучение темы "Показательная и логарифмическая функции" в ряде учебников, рекомендованных ФГОС начинается в 11 классе.

Тригонометрические функции, их основные свойства. Разложение синуса и косинуса в степенной ряд. Синус и косинус в комплексной области. Методика изучения тригонометрических функций в школьном курсе математики.

Функция синус

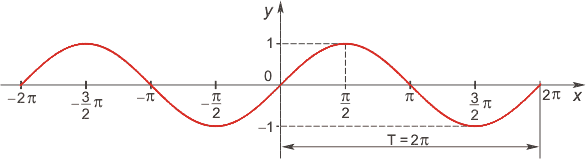Область определения: мн-во R всех действительных чисел. Область значений: отрезок [-1; 1]. Функция нечетная. График функции симметричен относительно начала координат. Функция периодическая с наименьшим положительным периодом 2π. Промежутки знакопостоянства: sin x = 0 при x = π·k, k ∈ Z; sin x > 0 при x ∈ (2π·k, π+2π·k), k ∈ Z; sin x < 0 при x ∈ (π+2π·k, 2π+2π·k), k ∈ Z. Наиб. значение функции sin x = 1 в точках: Наим. значение функции sin x = −1 в точках: Функция возрастает от −1 до 1 на промежутках: Функция убывает от −1 до 1 на промежутках:

Функция косинус

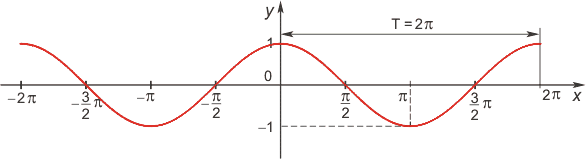
Область определения: R. Область значений: [-1; 1].

Функция четная. График функции симметричен относительно оси OY.

Период: 2π.

Промежутки знакопостоянства: cosx=0 при 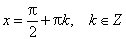; cos x > 0 при 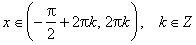; cos x < 0 при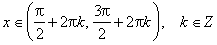

Наибольшее значение функции sin x = 1 в точках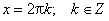

Наименьшее значение функции sin x = −1 в точках: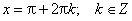

Функция возрастает от −1 до 1 на промежутках: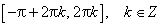

Функция убывает от −1 до 1 на промежутках: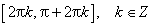

Функция тангенс

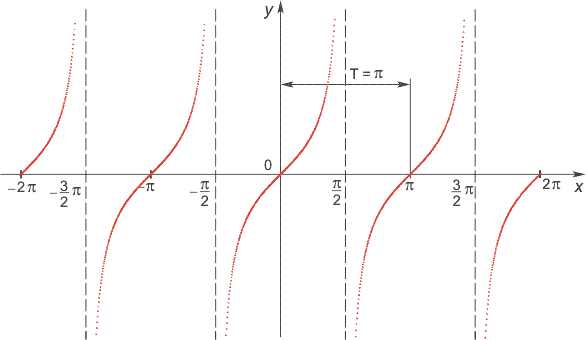
Область определения: объединение интервалов 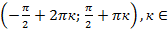Z.

Множество значений: вся числовая прямая, т.е. функция неограниченная.

Функция нечетная. График функции симметричен относительно оси OY.

Функция периодическая с наименьшим положительным периодом π, т.е. tg(x+π·k) = tg x, k ∈ Z для всех х из области определения. tg x = 0 при 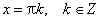; tg x > 0 при 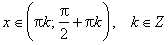; tg x < 0 при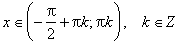

Экстремумов нет. Функция возрастает на каждом интервале области определения.

Функция котангенс

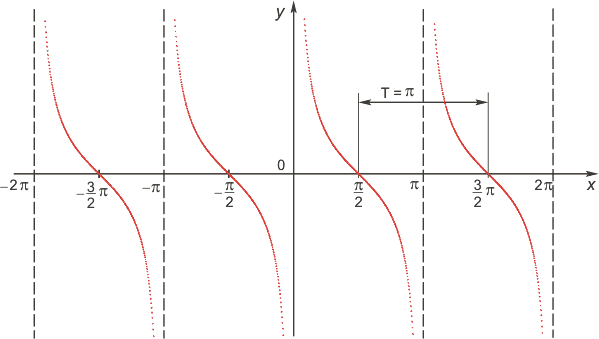
Область определения: объединение интервалов (pn; p+pn), nÎZ.

Множество значений: вся числовая прямая, т.е. функция неограниченная.

Функция нечетная. График функции симметричен относительно оси OY.

Функция периодическая с наименьшим положительным периодом π, т.е. ctg(x+π·k)=ctg x, k ∈ Z для всех х из области определения. ctg x = 0 при 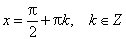; ctg x > 0 при 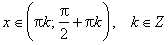; ctg x < 0 при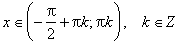

Экстермумов нет. Функция убывает на каждом интервале области определения.

Разложение синуса и косинуса в степенной ряд.

Рассмотрим тригонометрическую функцию f(x) = sinx. Она имеет производные всех порядков, вычисляемые по формулам 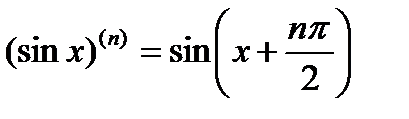и условия-теоремы 3, очевидно, выполняются, так как при всех х и п

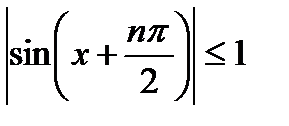Следовательно, sinx разлагается в ряд Тейлора и разложение справедливо при всех x. Найдем коэффициенты ряда Тейлора: 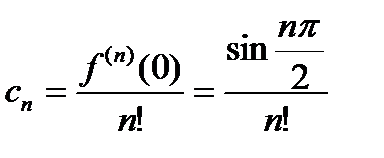;величина c_п зависит от четности или нечетности п:

, .

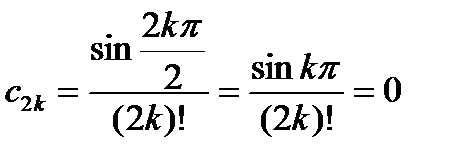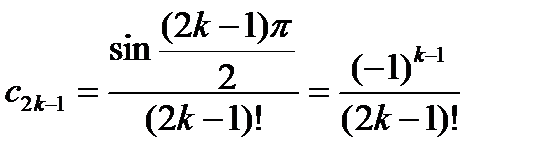Таким образом, при любых х верно разложение

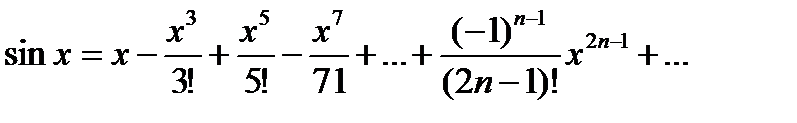(2)

Для тригонометрической функции f (x) = cosx можно так же, как это было сделано выше для sinx,получить разложение в ряд Тейлора, справедливое при любых х:

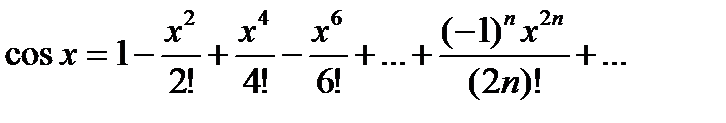(3)

Равенство (3) можно также считать определением функции cosх. Можно получить разложение (3) дифференцированием равенства (2).

Синус и косинус в комплексной области.

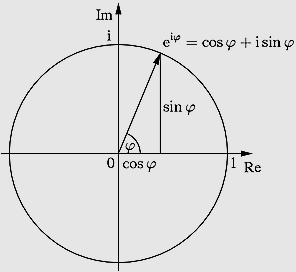
Формула Эйлера утверждает, что для любого действительного и комплексного числа х выполнено следующее равенство:

,

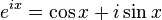где e — одна из важнейших математических констант, определяющаяся следующей формулой: 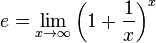, i — мнимая единица

.

Производные формулы

При помощи формулы Эйлера можно определить функции sin и cos следующим образом:

,

.

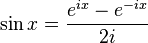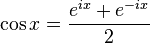Понятие тригонометрических функций комплексной переменной. Пусть 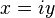, тогда:

,

.

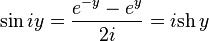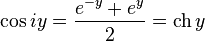Тождество Эйлера, связывающее пять фундаментальных математических констант:

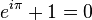является частным случаем формулы Эйлера при .

Методика изучения тригонометрических функций в школьном курсе математики.

Введение понятий sin a, cos a, tg aдля острого угла прямоугольного треугольника рассматривается: Погорелов - 8 кл. стр. 102,108; Атанасян - 8 кл. стр. 180.

Изучение тригонометрических функций sina, cosa, tgaдля угла a Î [0, 180]: Погорелов - 8 кл. стр. 132, Атанасян - 9 кл. стр.239.

При введении данных понятий используется окружность радиуса R (Погорелов) и R=l (Атанасян), взятая на координатной плоскости. От положительного направления оси х откладываем значения угла a. Используя определения для прямоугольного треугольника, получаем: ;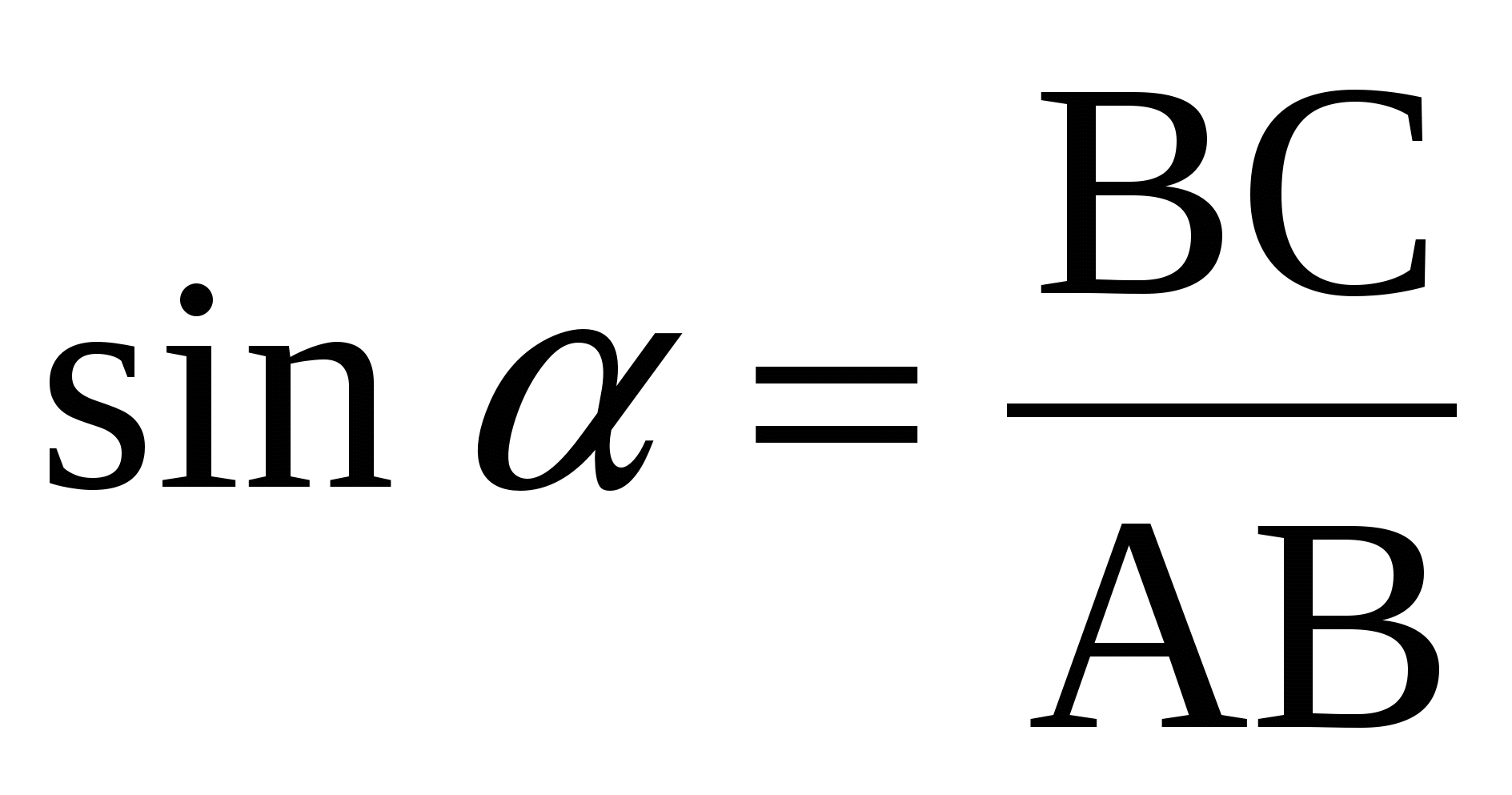

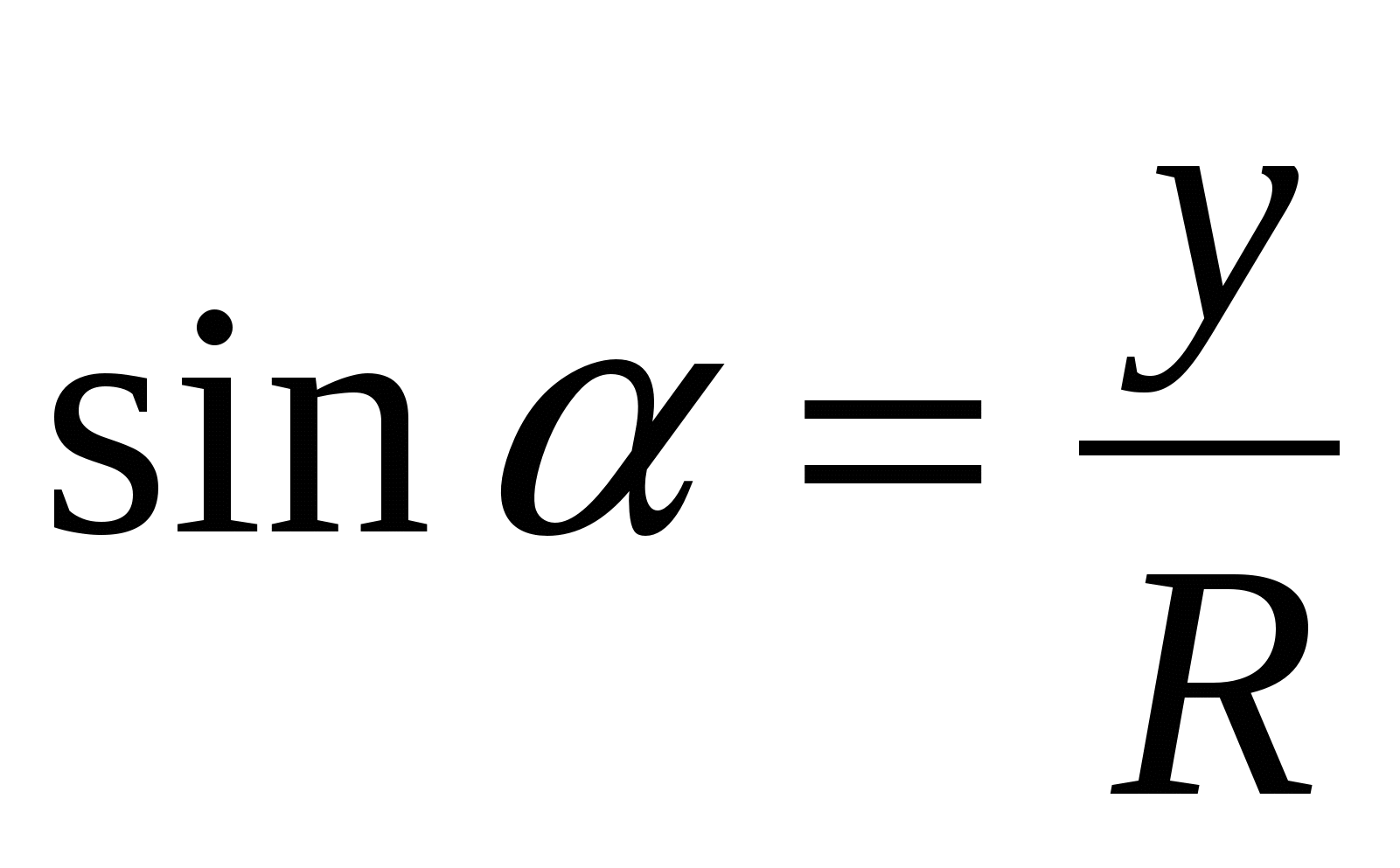(Погорелов); sin a = у (Атанасян).

Основными целями изучения тригонометрических функций числового аргумента являются:

1) ознакомление учащихся с новым видом трансцендентных функций;

2) развитие навыков вычислительной практики (работа с трансцендентными функциями зачастую требует громоздких вычислений);

3) наглядная иллюстрация всех основных свойств функций (в особенности периодичности);

4) установление межпредметных связей с практикой (изучение колебаний маятника, электрического тока, волновой теории света невозможны без знаний о тригонометрических функциях);

5) развитие логического мышления (обилие формул порождает необходимость преобразований не алгебраического характера, которые носят исследовательский характер).

В изучении тригонометрических функций можно выделить следующие этапы:

I. Первое знакомство с тригонометрическими функциями углового аргумента в геометрии. Значение аргумента рассматривается в промежутке (0^о;90^о). На этом этапе учащиеся узнают, что sin, сos, tg и ctg угла зависят от его градусной меры, знакомятся с табличными значениями, основным тригонометрическим тождеством и некоторыми формулами приведения.

II. Обобщение понятий синуса, косинуса, тангенса и котангенса для углов (0^о;180^о). На этом этапе рассматривается взаимосвязь тригонометрических функций и координат точки на плоскости, доказываются теоремы синусов и косинусов, рассматривается вопрос решения треугольников с помощью тригонометрических соотношений.

III. Введение понятий тригонометрических функций числового аргумента.

IV. Систематизация и расширение знаний о тригонометрических функциях числа, рассмотрение графиков функций, проведение исследования, в том числе и с помощью производной.

Отметим, что существует несколько способов определения тригонометрических функций. Их можно подразделить на две группы: аналитические и геометрические. К аналитическим способам относят определение функции у = sin х как решения дифференциального уравнения f ^''(х)=-c*f(х) или как сумму степенного ряда sin х = х – х³ /3!+ х⁵ /5! – …

К геометрическим способам относят определение тригонометрических функций на основе проекций и координат радиус-вектора, определение через соотношения сторон прямоугольного треугольника и определения с помощью числовой окружности. В школьном курсе предпочтение отдается геометрическим способам в силу их простоты и наглядности.

Отметим, что изучение тригонометрических функций в школьном курсе имеет некоторые особенности. Во-первых, до изучения тригонометрических функций, рассматривались функции вида у=f(x), где х и у – некоторые действительные числа, здесь же - углу ставится в соответствие число, что является несколько непривычным для учащихся. Кроме того, раньше все функции задавались формулами, в которых явным образом был указан порядок действий над значениями аргумента для получения значений функции. Теперь же учащиеся сталкиваются с функциями, заданными таблично.

Таким образом, изучая тригонометрические функции, учащиеся лучше начинают разбираться в сущности самого понятия функции. Они начинают осознавать, что функцией может быть зависимость между любыми множествами объектов, даже если они имеют различную природу (лишь бы каждому значению аргумента соответствовало единственное значение функции).