Группа подобия и ее подгруппы.
Пусть P – множество всех преобразований подобия плоскости, и на нем задана некоторая операция «∙».
Множество Р является группой относительно этой операции.
Действительно:
- Если f
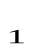 , f
, f 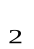
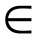 P , то f
P , то f 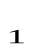 ∙ f
∙ f 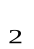
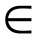 P ;
P ; - Если f
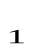
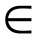 P , то f
P , то f 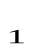
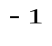
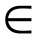 P.
P. - Основным инвариантом группы является мера угла.
Подобие первого рода образует подгруппу группы Р. Множество гомотетий с коэффициентом k (равным коэффициенту подобия) образует подгруппу группы Р.
Множество подобий второго рода не образует подгруппу, т.к. произведение подобий второго рода дает подобие первого рода.
Основные вопросы методики изучения преобразования фигур в основной школе.
Учащиеся знакомы с реальными предметами, дающими наглядное представление о подобных фигурах (географические карты) Основная цель изучения преобразования подобия – сформировать понятие подобных треугольников, выработать умение применять признаки подобия треугольников.
А.В.Погорелов – 9 класс тема «Подобие фигур» (17ч) Л.С.Атанасян – 8 класс тема «Подобные треугольники» (19ч) И.Ф.Шарыгин – 8 класс тема «Подобие» (20ч)
По А.В. Погорелову на изучение подобия фигур отводится 17 часов. Изучается в 9 классах до изучения тем площади. Подобие фигур разделено на 9 тем. В конце главы вводится углы, вписанные в окружность и пропорциональность отрезков хорд и секущих окружности. В начале дается понятие гомотетии и подобии фигур. Затем рассматривается подобие треугольников, признаки подобия треугольников, подобие прямоугольных треугольников.
Определение (А.В. Погорелов). Преобразование фигур F называется преобразованием подобия если при этом преобразование расстояния между точками изменяется в одно и то же число раз, то есть для любых двух точек X и Y фигуры F и точки X’ и Y’ фигуры F’, в которые они переходят, XY=кXY’.
Две фигуры называются подобными, если они переводятся одна в другую преобразованием подобия.
Признаки подобия треугольников. Два треугольника подобны, если:все их соответственные углы равны (достаточно равенство двух углов);все их стороны пропорциональны;две стороны одного треугольника пропорциональны двум сторонам другого, а углы, заключенные между этими сторонами, равны.
Два прямоугольных треугольника подобны, если:их катеты пропорциональны;катет и гипотенуза одного треугольника пропорциональны катету и гипотенузе другого;два угла треугольника равны двум углам другого.
Площади подобных фигур пропорциональны квадратам их сходственных линий (например, сторон). Так, площади кругов пропорциональны отношению квадратов их диаметров (или радиусов).
По Л.С. Атанасяну в главе 7 подобные треугольники отводится 19 часов. Основное внимание в главе уделено подобным треугольникам. Изучается в 8 классах после глав четырехугольники и площади.
Определение подобных треугольников дается на основе теоремы об отношении площадей треугольников, имеющих по равному углу, весьма просто доказываются признаки подобия треугольников. Они широко используются в курсе геометрии. Кроме того, материал, связанный с подобием, позволяет содержательно реализовать межпредметные связи с алгеброй (пропорциональность, уравнения, квадратные корни) и с физикой (например, геометрическая оптика). В конце главы вводится синус, косинус и тангенс острого угла прямоугольного треугольника.
При изучении данной темы нужно иметь в виду, что свойства подобных фигур будут многократно применяться при дальнейшем изучении курса геометрии. Поэтому следует уделить значительное внимание и время решению задач, направленных на формирование умений доказывать подобие треугольников с использованием признаков и вычислять элементы подобных треугольников.
При изучении признаков подобия достаточно доказать два признака, так как первый доказывается с опорой на теорему об отношении площадей треугольников, имеющих равные углы, а доказательства двух других аналогичны. Применение метода подобия треугольников к доказательствам теорем учащиеся изучают на примере теоремы о средней линии треугольника. С учащимися интересующимися математикой можно рассмотреть задачи на построение методом подобия.
После изучения подобных треугольников рассматривается вопрос о подобии произвольных фигур на интуитивной основе.
В курсе стереометрии в начале 11 класса 9 в параграфе «Преобразование подобия» (не обязательный пункт для изучения на базовом уровне) дается следующее определение (Л.С. Атанасян): Преобразования подобия с коэффициентом к >0 называется отображениепространства на себя. При котором любые точки А и В переходят в такие точки А1, В1, что А1=кВ1.
Два тела называются подобными, если существует такое преобразование подобия, при котором одно из них переходит в другое.
Таким образом, мы рассмотрели два способа изучения подобия треугольников: можно рассмотреть подобные треугольники как частные случаи подобных фигур (А.В.Погорелов) или можно определить подобные треугольники как треугольники, имеющие соответственно пропорциональные стороны и соответственно равные углы (Л.С.Атанасян).
7.9 Аффинные преобразования плоскости. Группа аффинных преобразований и ее подгруппы. Различные подходы к введению понятия преобразования фигур в основной школе.
Аффинные преобразования плоскости.
Определение. Преобразование плоскости 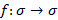 называется аффинным, если оно любые три точки А, В, С, лежащие на одной прямой, переводит в три точки A’,B’,C’ (A
называется аффинным, если оно любые три точки А, В, С, лежащие на одной прямой, переводит в три точки A’,B’,C’ (A 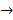 A’, B
A’, B 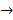 B’, C
B’, C 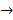 C’), лежащие на одной прямой, и при этом сохраняется простое отношение трех точек: (А, В, С)=(A’, B’, C’)=
C’), лежащие на одной прямой, и при этом сохраняется простое отношение трех точек: (А, В, С)=(A’, B’, C’)= 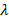 .
.
Теорема. Рассмотрим любые два аффинных преобразования 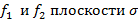 . Если для любых двух точек
. Если для любых двух точек 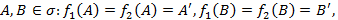 то для любой точки М прямой АВ (
то для любой точки М прямой АВ ( 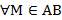 ) выполняется равенство:
) выполняется равенство: 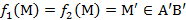 .
.
Основная теорема. Пусть R= 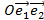 и R’=
и R’= 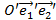 – любые два репера плоскости
– любые два репера плоскости 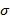 . Тогда существует единственное аффинное преобразование
. Тогда существует единственное аффинное преобразование 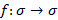 , которое переводит репер R и R’ и при этом любая точка М с координатами (х,у) в репере R переходит в точку М’ с теми же координатами в репере R’ (
, которое переводит репер R и R’ и при этом любая точка М с координатами (х,у) в репере R переходит в точку М’ с теми же координатами в репере R’ ( 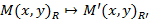 ).
).
Доказательство: существование. Построим преобразование 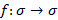 по закону
по закону 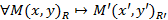 , тогда
, тогда 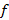 – биекция, а значит
– биекция, а значит 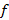 - преобразование плоскости
- преобразование плоскости 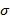 . На произвольной прямой
. На произвольной прямой 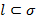 рассмотрим любые три точки:
рассмотрим любые три точки: 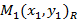 ,
, 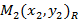 ,
, 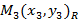 . По заданному закону:
. По заданному закону: 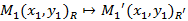 ,
, 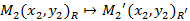 ,
, 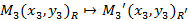 . Пусть
. Пусть 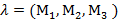 , тогда
, тогда 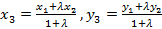 . Но по введенному закону эти же соотношения сохраняются и для точек
. Но по введенному закону эти же соотношения сохраняются и для точек 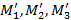 (координаты точек в репере R’ – те же числа, что и в репере R), следовательно, все три точки лежат на одной прямой
(координаты точек в репере R’ – те же числа, что и в репере R), следовательно, все три точки лежат на одной прямой 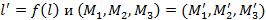 откуда (по определению)
откуда (по определению) 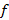 - аффинное преобразование плоскости
- аффинное преобразование плоскости 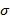 .
.
Теорема. Любое аффинное преобразование плоскости 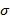 либо сохраняет ориентацию плоскости, либо меняет ориентацию.
либо сохраняет ориентацию плоскости, либо меняет ориентацию.
Аналитическое выражение аффинного преобразования плоскости.
Теорема. Преобразование плоскости 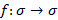 - аффинное преобразование тогда и только тогда, когда в некоторой АСК
- аффинное преобразование тогда и только тогда, когда в некоторой АСК 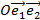 преобразование
преобразование 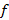 задано аналитически:
задано аналитически:
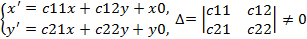 .
.
Свойства аффинных преобразований:
1. Прямая переходит в прямую, отрезок – в отрезок, луч – в луч, полуплоскость – в полуплоскость, угол – в угол, параллельные прямые – в параллельные прямые.
2. Сохраняется простое отношение в трех точек, а следовательно, середина отрезка переходит в середину отрезка.
3. Любое аффинное преобразование либо сохраняет ориентацию плоскости (преобразование 1 рода), либо меняет ориентацию (преобразование 2 рода).
Группа аффинных преобразований и ее подгруппы.
Теорема. Обозначим через 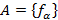 - множество всех аффинных преобразований плоскости
- множество всех аффинных преобразований плоскости 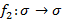 . Обозначим
. Обозначим  - композицию данных преобразований. Пара (А,
- композицию данных преобразований. Пара (А,  ) – группа.
) – группа.
Группа (А,  ) называется группой аффинных преобразований плоскости. Основной инвариант этой группы – простое отношение трех точек.
) называется группой аффинных преобразований плоскости. Основной инвариант этой группы – простое отношение трех точек.
Подгруппы группы А.
1. 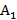 – множество всех аффинных преобразований 1 рода.
– множество всех аффинных преобразований 1 рода.
2. 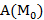 - множество всех аффинных преобразований, для которых
- множество всех аффинных преобразований, для которых 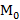 - неподвижная точка.
- неподвижная точка.
Аффинные преобразования плоскости, обладающие единственной неподвижной точкой, называется центроаффинными.
3. А(l) – множество всех аффинных преобразований, для которых l – прямая неподвижных точек.
4. Р – подобие.
5. D – движение.
6. множество всех аффинных преобразований, сохраняющих площадь S фигуры 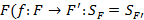 . Такие аффинные преобразования называют эквиаффинными, а данную подгруппу – эквиаффинной подгруппой аффинной группы.
. Такие аффинные преобразования называют эквиаффинными, а данную подгруппу – эквиаффинной подгруппой аффинной группы.
Различные подходы к введению понятия преобразования фигур в основной школе.
