Группа движений плоскости и ее подгруппы

Пусть D – множество всех движений, рассмотренных на плоскости, и на нем задана некоторая операция « ∙ ».

Множество D является группой относительно этой операции.

Действительно:

- если движение h, g 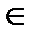D , то h∙g 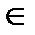D;

- если h 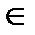D , то h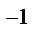 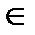D.

- основным инвариантом группы D является сохранение расстояний между точками.

Группа движений первого рода является подгруппой всей группы движений D. Группа движений второго рода не является подгруппой группы D, так как произведение двух движений второго рода является движением первого рода.

Теорема.Произведение двух осевых симметрий S₁ и S₂, где 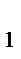S S 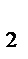= O, есть порот плоскости вокруг т.O на угол, величина которого равна удвоенной величине угла, образованного прямыми S₁,S_2.

Теорема.(обратная теорема). Всякий поворот плоскости вокруг точки на угол α 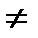0 можно разложить в произведение двух осевых симметрий, оси которых будут пересекаться в центре поворота и образовывать угол φ = α/2.

Теорема. Произведение двух осевых симметрий, оси которых S₁ и S₂ параллельны и различны, есть параллельный перенос на вектор p длина которого равна удвоенному расстоянию между прямыми S₁ и S₂. Теорема.(обратная теорема).Всякий параллельный перенос на вектор 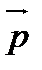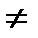0 можно разложить в виде произведения двух осевых симметрий, ос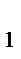и S и S 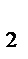которых параллельны и = .

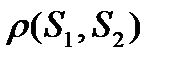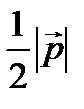Теорема. Всякое движение плоскости можно представить в виде произведения не более трех осевых симметрий. Если движение не разлагается в произведение, значит, оно есть осевая симметрия.

Методика. Обучение решению задач с помощью геометрических преобразований в основной школе.

Общий прием решения задачи методом геометрического преобразования:

На этапе изучения содержания задачи уяснить взаимное расположение данных (данных и искомых) точек или фигур (или их частей и элементов);

На этапе анализа (поиска решения) – в предположении, что задача решена, сделать (если нужно) эскиз, установить связи между данными задачи и искомыми (точками, фигурами, их элементами или свойствами), выбрать геометрическое преобразование, которое позволит обосновать наличие того или иного отношения между объектами (точками, фигурами).

Указать (или выполнить) выбранное преобразование так, чтобы один объект переходил в другой (или построить вспомогательную фигуру)

В задаче на доказательство – обосновать наличие указанного отношения между объектами с помощью свойств выбранного преобразования;

Задачи с геометрическими преобразованиями учащиеся встречают на разных этапах обучения:

1) в 5-6 классах изучаются отдельные виды преобразований, такие как осевая и центральная симметрия; на этом этапе от учащихся требуется умение строить образ точки (фигуры) при осевой, либо центральной симметрии, находить центр, либо ось симметрии;

2) в 7-9 классах начинается систематическое изучение всех видов геометрических преобразований; на этом этапе учащиеся должны знать определение каждого вида преобразования, его свойства, уметь решать задачи.

7.8 Преобразования подобия плоскости. Группа преобразований и ее подгруппы. Основные вопросы методики изучения преобразования фигур.

Опр. Преобразование плоскости называется преобразованием подобия, если k > 0, что для любых двух точек А и B и их образов A` и B` выполняется равенствоA`B`=kAB. k-коэф-т подобия.

При k =1 преобразование подобия сохраняет расстояние, т.е. является движением. Значит, движение– частный случай подобия.

Опр.Преобразование плоскости называется гомотетией, если существует некоторое число m 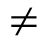1, что для любых трех точек плоскости М, М 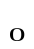,M` выполняется условие .

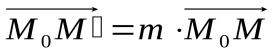Точка М 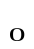- центр гомотетии, число m – коэффициент гомотетии. Если m > 0 – гомотетия положительна, если m < 0 – гомотетия отрицательна.

Теорема 16.3. Гомотетия есть подобие.

Доказательство:

1. Рассмотрим гомотетию 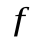с центром 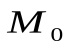и коэффициентом m: , .

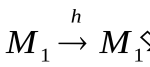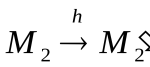2. По определению гомотетии имеем: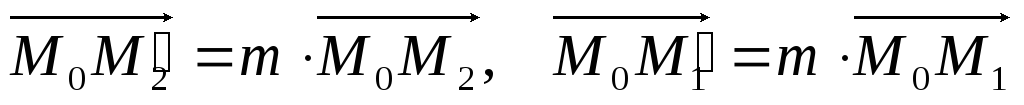

3. Вычтем из первого равенства второе: 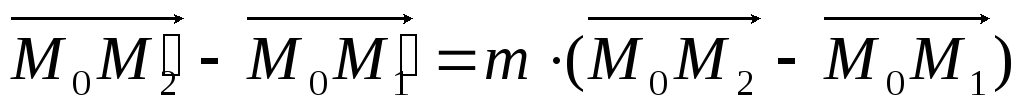, 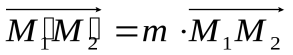. Значит, гомотетия 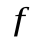есть подобие, где коэффициент гомотетии 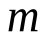равен коэффициенту подобия .

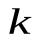• Если m = 1, то гомотетия есть тождественное преобразование.
• Если m =-1, то гомотетия есть центральная симметрия с центром в точке М .
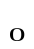• Если |m| 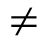1, то гомотетия есть преобразование подобия, отличное от движения, т.е. преобразование, не сохраняющее расстояний.

Если точка М (x, у) при гомотетии 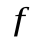переходит в точку M`(x`,y`), то: 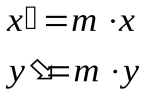- аналитические выражения гомотетии.

Свойства гомотетии

1. Гомотетия с коэффициентом, отличным от 1, переводит прямую, не проходящую через центр гомотетии, в прямую, ей параллельную; прямую, проходящую через центр – в себя.
2. Гомотетия сохраняет простое отношение трех точек.
3. Гомотетия сохраняет ориентацию плоскости.
4. Гомотетия переводит угол в равный ему угол.

Т.Пусть f – преобразование подобия с коэффициентом k > 0, а h – гомотетия с коэффициентом k и центром в точке М 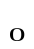. Тогда существует единственное движение g такое, что f = g∙h.

Док=во:

1. Рассмотрим некоторое движение g, представимое как g = f h 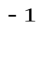(*), где .

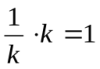Рассмотрим композицию движения 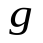и гомотетии 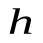(помножим обе части равенства (*) на гомотетию 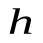): 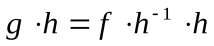илиg∙h = f (**)

1. Покажем, что движение 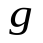единственно:

• Пусть существует движение g , такое, что 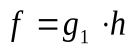. Тогда 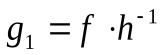g =f h . Но 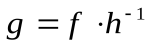. Значит,g = g.

Гомотетия обладает всеми свойствами движений, подобие также обладает всеми свойствами движений.

Так как гомотетия сохраняет ориентацию, а подобие есть произведение движения на гомотетию, т.е. движение имеет одну ориентацию с гомотетией, то подобие также имеет эту ориентацию. В этом случае говорят о подобии 1-го рода.

Если движение имеет ориентацию, противоположную гомотетии, то в этом случае подобие имеет противоположную ориентацию и является подобием 2-го рода.