Основы логики. Основные логические операции. Логические выражения и таблицы истинности. Логические законы. Методика.

ОСНОВЫ ЛОГИКИ

Логика – наука о законах и формах мышления

Высказывание (суждение) – некоторое предложение, которое может быть истинно (верно) или ложно

Утверждение – суждение, которое требуется доказать или опровергнуть

Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом

Умозаключение – логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение

Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0)

Сложное логическое выражение – логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью логических операций

ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ

· Логическое отрицание {инверсия).A, не А.

· Логическое умножение {конъюнкция).А&В, A and В, А*В, А^В

Высказывание А ^ В истинно тогда и только тогда, когда оба высказывания А и В истинны.

· Логическое сложение {дизъюнкция).A v В, A or В, А + В, А или В.
Высказывание A v В ложно тогда и только тогда, когда оба высказывания А и В ложны.
Остальные операции алгебры логики выражаются через первые три опе­рации: отрицание, конъюнкцию и дизъюнкцию.

· Логическое следование {импликация).А > В, А => В.
Высказывание А > В ложно только тогда, когда А истинно, а В ложно.
Импликация выражается через дизъюнкцию и отрицание: А => В = A v В.

· Эквивалентность (равносильность, необходимо и достаточно, тогда и только тогда).А ~ В, А <=> В, А = В.
Высказывание А <=> В истинно тогда и только тогда, когда значения А и В совпадают.
Эквивалентность выражается через отрицание, дизъюнкцию и конъюнкцию: А <=> В = (А v В) ^ (B v А).

ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ТАБЛИЦЫ ИСТИННОСТИ.

Таблица истинности - таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.

Логическое выражение - составные высказывания в виде формулы.

Алгоритм построения таблицы истинности:

1. подсчитать количество переменных n в логическом выражении;

2.определить число строк в таблице по формуле m=2ⁿ, где n - количество переменных;

3.подсчитать количество логических операций в формуле;

4.установить последовательность выполнения логических операций с учетом скобок и приоритетов;

5.определить количество столбцов: число переменных + число операций;

6.выписать наборы входных переменных;

7.провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.

1) Логическое умножение или конъюнкция:

Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными

А	В	А^В

Логическое сложение или дизъюнкция:

Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.

А	В	А vВ

Логическое отрицание или инверсия:

Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот если исходное ложно, то будет истинным.

А	Не А

Логическое следование или импликация:

Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь.

А	В	А=>В

Логическая равнозначность или эквивалентность:

Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.

А	В	А<=>В

ЛОГИЧЕСКИЕ ЗАКОНЫ

А = А– закон тождества

Любое высказывание (мысль, понятие, суждение) на протяжении всего рассуждения должно сохранять один и тот же смысл.

А & 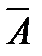= 0– закон непротиворечия

Два несовместимых друг с другом суждения не могут быть одновременно истинными; как минимум одно из них ложно.

A Ú 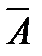= 1– закон исключенного третьего

Если в одном из двух выражений что-либо о предмете утверждается, а во втором отрицается – одно из них обязательно истинно.

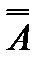= А – закон двойного отрицания

отрицание отрицания даёт утверждение.

Свойства констант:

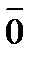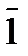= 1 = 0

А Ú 0 = А А & 0 = 0

А Ú 1 = 1 А & 1 = 1

Законы идемпотентности:

А Ú А = А

А & А = A

Законы коммутативности:

А Ú В = В Ú А

А & В = В & А

Законы ассоциативности:

А Ú (В Ú С) = (АÚ В) Ú С

А & (В & С) = (А & В) & С

Законы дистрибутивности:

А Ú (В & С) = (АÚ В) & (А Ú С)

А & (В Ú С) = (А & В) Ú (А& С)

Законы поглощения:

А Ú (А & В) = А

А & (А Ú В) = А

Законы де Моргана:

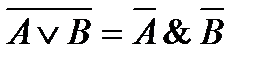
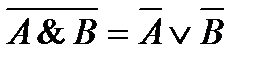
Методика

Босова 8кл., 5ч.Раздел математические основы информатики. Вопросы: Высказывание. Логические операции, Построение таблиц истинности для логических

Выражений, Свойства логических операций, Решение логических задач, Логические элементы(построение логических схем.)

Семакин 9 кл, часы ?

Угринович 9кл, 4ч. Логика и логические основы компьютера (2 часа на алгебру логики). Практическая: таблицы истинности логических функций.