Пределы. Замечательные пределы 1,2

Следствия из первого замечательного предела

1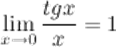

2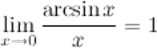

3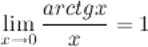

4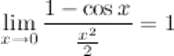

Применение первого замечательного предела:

Второй замечательный предел

Точки разрыва. Св-ва

Точка k, в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:

1 функция 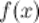определена в точке и ее окрестности;

2 существует конечный предел функции 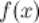в точке k;

3 это предел равен значению функции в точке k, т.е.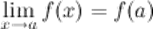

называется точкой разрыва функции.

Если в точке k нарушено условие непрерывности и односторонние пределы конечные но не равны - называется точкой разрыва первого рода.

Если хотя б один из пределов f (k+0) или f (k-0) не существует или равен бесконечности, то точка k называется точкой разрыва второго рода.

Если существуют левые и правый пределы и они равны друг другу но не совпадают со значением функции точки k то точка k называется точкой устранимого разрыва

Односторонние пределы

Односторонние пределы — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.

Число 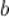называется правым пределом функции 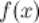в точке 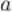, если для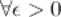 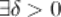такое, что для любого 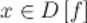и , выполняется неравенство 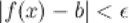(рис. 1). Правый предел обозначается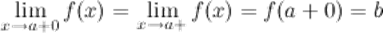

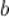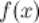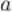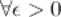
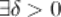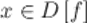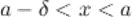Число называется левым пределом функции в точке , если для такое, что для любого и , выполняется неравенство 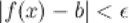(рис. 2). Левый предел обозначается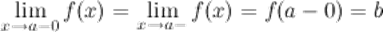

Производная.

Производной 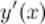от функции 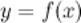в точке 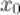называется предел отношения приращения функции 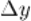к приращению аргумента 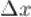: 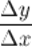при , если он существует, то есть:

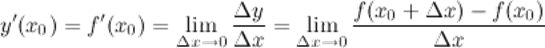
или

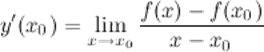
Таблица производных

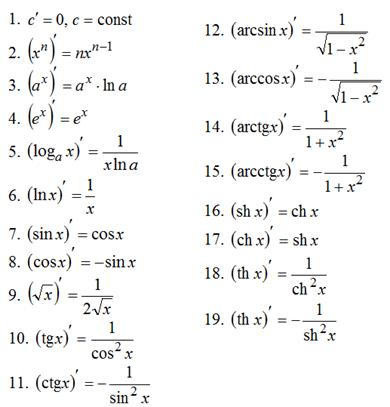
Правила дифференцирования

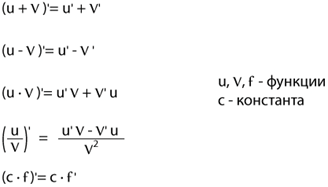
Исследование функции

Структура:

4 Область определения 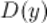и область допустимых значений 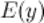функции.

5 Четность, нечетность функции.

6 Точки пересечения с осями.

7 Асимптоты функции.

8 Экстремумы и интервалы монотонности.

9 Точки перегиба и промежутки выпуклости, вогнутости.

10 Сводная таблица.

Функции. Построение графика функции

Фу́нкция — в математике соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу одного множества ставится в соответствие некоторый элемент из другого множества.

Интеграл

Основные формулы

Совокупность всех первообразных функции 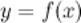, определенных на заданном промежутке, называется неопределенным интегралом от функции 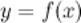и обозначается символом .

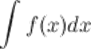То есть

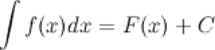
Знак 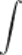называется интегралом, 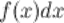- подынтегральным выражением, 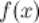- подынтегральной функцией, а 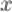- переменной интегрирования.

Операция нахождения первообразной или неопределенного интеграла от функции 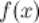называется интегрированием функции .

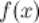Методы интегрирования

· Разложение

· Введение нового аргумента

· Интегрирование дробно-рациональных функций

48. Определённый интеграл — это форма ограниченная слева и справа прямыми а и b снизу осью ОХ сверху графиком функции f(x)

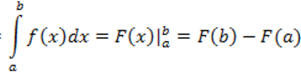
49. Криволинейные трапеции - называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a;b] функции f, осью Ox и прямыми x = a и x = b.

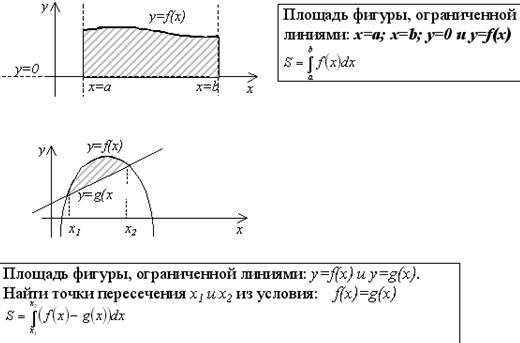
50. Вычисление площадей

.

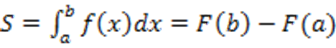Найти площадь фигуры, ограниченной линиями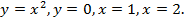

Вот искомая площадь:

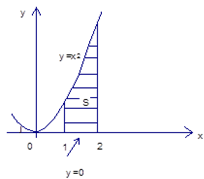
Вот формула: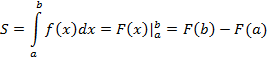

Пределы интегрирования .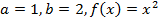

= .

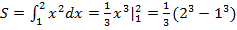Вычислили площадь криволинейной фигуры. Ответ: