Свойства умножения матрицы на число

Матрица

Матрица - это таблица данных, которая берется в круглые скобки.

Квадратная матрица

Квадратной матрицей называется матрица, у которой количество строк равно количеству столбцов (размера n×n), число n называется порядком матрицы.

Диагональная матрица

Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.

4. Матричная строка, столбец –

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов задает размер матрицы.

Количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

Единичная матрица

Единичной матрицей называется диагональная матрица, диагональные элементы которой равны 1.

6. Равные матрицы - Матрицы называются равными, если у них одинаковое число строк и столбцов и все соответствующие элементы совпадают.

Сложение матрицы

Сложение матриц (сумма матриц) A + B есть операция вычисления матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен:

сij = aij + bij

Умножение матриц

Произведением матрицы на матрицу называется матрица такая, что элемент матрицы , стоящий в -ой строке и -ом столбце, т.е. элемент , равен сумме произведений элементов -ой строки матрицы на соответствующие элементы -ого столбца матрицы .

Замечание

Умножать матрицы можно тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.

Умножение на число

Свойства умножения матрицы на число

1 · A = A

0 · A = Θ, где Θ - нулевая матрица

k · (A + B) = k · A + k · B

(k + n) · A = k · A + n · A

(k · n) · A = k · (n · A)

Найти произведение матрицы A = ( 4 2 ) и числа 5.

( 9 0 )

Решение:

5·A= 5· ( 4 2 ) = ( 5·4 5·2 ) = ( 20 10 )

( 9 0 ) ( 5·9 5·0 ) ( 45 0 )

Транспонированная матрица

Транспонирование матрицы - это операция над матрицей, при которой ее строки и столбцы меняются местами:

aTij = aji

A=					.

Решение:

AT=

Обратная матрица

Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице E:

A·A-1 = A-1·A = E

Свойства обратной матрицы:

1

2

3

4

Обратная матрица существует только для квадратных матриц с не равными нулю определителями.

12. Определители

A = ( 5 7 )

-4 1

Решение:

det(A) = (5 7)

(-4 1 ) = 5·1 - 7·(-4) = 5 + 28 = 33

Порядка

Го порядка

A = ( 5 7)

(-4 1)

Решение:

det(A) = (5 7)

(-4 1 ) = 5·1 - 7·(-4) = 5 + 28 = 33

Го порядка

∆ =

a11 a12 a13 a21 a22 a23 a31 a32 a33

=

= a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ - a₁₃·a₂₂·a₃₁ - a₁₁·a₂₃·a₃₂ - a₁₂·a₂₁·a₃₃

Линейные уравнения

из первого уравнения выразим:

Полученное выражение подставляем во второе уравнение:

Раскрываем скобки, приводим подобные слагаемые и находим значение :

Далее вспоминаем про то, от чего плясали:

Значение нам уже известно, осталось найти:

Ответ:

Векторы

Вектор это направляющий отрезок для которого указано какой из его концов является началом, а какой концом

16. Нулевой вектор – если начало и конец вектора совпадают

17. Длина вектора – расстояние между его началом и концом

18. Коллинеарные векторы – два ненулевых вектора, если они лежат на одной прямой или на параллельных прямых

19. Равные векторы – векторы которые сонаправленны и их длины равны

Через cos

Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

Задание. Вычислить скалярное произведение векторов и , если их длины соответственно равны 2 и 3, а угол между ними 60°.

Решение. Так как из условия , , а , то

Свойства скалярного произведения:

1 - симметричность.

2 . Обозначается и называется скалярный квадрат.

3 Если , то

4 Если и и , то . Верно и обратное утверждение.

5

6

7

26. Длина вектора в координатах – длина направленного отрезка которая определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.

27. Длина отрезка - Это расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек

d²= (х₂— х₁)²+ (y₂— y₁)²

Извлекая квадратный кореньиз выражения, находим:

|AB|² = (y₂ – y₁)² + (x₂ – x₁)².

Уравнения прямой и кривых

(x−x_A)²+(y−y_A)²=(x−x_B)²+(y−y_B)² – уравнение прямой

a₁₁x² + 2a₁₂xy + a₂₂y² + 2a₁x +2a₂y +a = 0 - Общее уравнение кривой второго порядка имеет вид

Общий вид уравнения прямой

Ax + By + C = 0.

Уравнение окружности

Мы имеем формулу для расчёта расстояния между двумя точками, если знаем координаты точек ∣AB∣=√(x_A−x_B)²+(y_A−y_B)², а если так, то квадрат расстояния AB²=( x_A−x_B)²+(y_A−y_B)².

Эллипс. Фокус Эллипса

Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух заданных точек F₁ и F₂ , называемых фокусами эллипса, есть величина постоянная.

36. Гипербола- геометрическое место точек, для каждой из которых модуль разности расстояний от нее до двух данных точек F₁,F₂ (фокусы) есть величина постоянная, равная 2a.

Элементы гиперболы:
A₁A₂=2a - действительная ось
B₁B₂=2b - мнимая ось
A₁ ,A₂ - вершины
F₁(c ; 0), F₂(-c ; 0) - фокусы
F₁F₂=2c - фокальное расстояние (фокусное расстояние)

c²=a²+b²

Уравнение :

Парабола

Формула параболы y=ax²+bx+cесли а>0 то ветви параболы направленны вверх,
а<0 то ветви параболы направлены вниз.
Свободный член c эта точке пересекается параболы с осью OY;

Вершина параболы, ее находят по формуле x=(-b)/2a, найденный x подставляем в уравнение параболы и находим y;

Нули функции или по другому точки пересечения параболы с осью OX они еще называются корнями уравнения. Чтобы найти корни мы уравнение приравниваем к 0 ax2+bx+c=0;

Виды уравнений:

a) Полное квадратное уравнение имеет вид ax2+bx+c=0 и решается по дискриминанту;

b) Неполное квадратное уравнение вида ax2+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:

ax2+bx=0,

х(ax+b)=0,

х=0 и ax+b=0;

c) Неполное квадратное уравнение вида ax2+c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);

38. Способы задания функции. Предел функции

Табличный способ. Заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Применяется когда область определения функции является дискретным конечным множеством.

При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента.

Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.

Пример:

Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Чтобы графическое задание функции было корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением.

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.

Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.

Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.

Точки разрыва. Св-ва

Точка k, в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:

1 функция 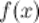определена в точке и ее окрестности;

2 существует конечный предел функции 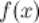в точке k;

3 это предел равен значению функции в точке k, т.е.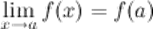

называется точкой разрыва функции.

Если в точке k нарушено условие непрерывности и односторонние пределы конечные но не равны - называется точкой разрыва первого рода.

Если хотя б один из пределов f (k+0) или f (k-0) не существует или равен бесконечности, то точка k называется точкой разрыва второго рода.

Если существуют левые и правый пределы и они равны друг другу но не совпадают со значением функции точки k то точка k называется точкой устранимого разрыва

Односторонние пределы

Односторонние пределы — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.

Число 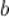называется правым пределом функции 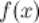в точке 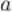, если для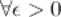 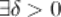такое, что для любого 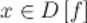и , выполняется неравенство 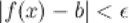(рис. 1). Правый предел обозначается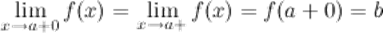

Число 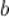называется левым пределом функции 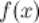в точке 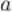, если для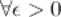 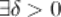такое, что для любого 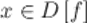и 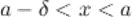, выполняется неравенство 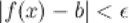(рис. 2). Левый предел обозначается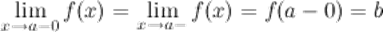

Производная.

Производной 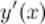от функции 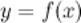в точке 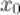называется предел отношения приращения функции 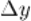к приращению аргумента 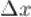: 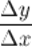при , если он существует, то есть:

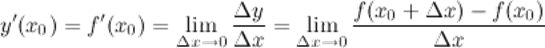
или

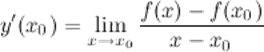
Таблица производных

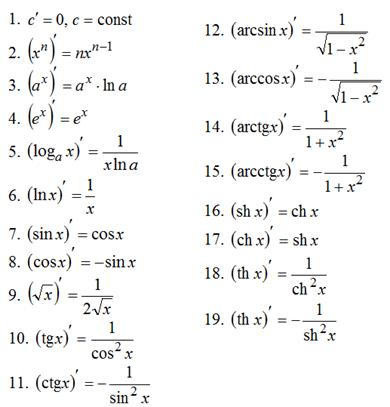
Правила дифференцирования

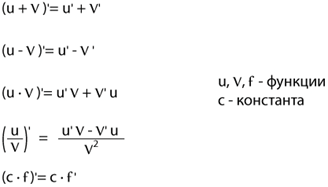
Исследование функции

Структура:

4 Область определения 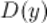и область допустимых значений 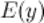функции.

5 Четность, нечетность функции.

6 Точки пересечения с осями.

7 Асимптоты функции.

8 Экстремумы и интервалы монотонности.

9 Точки перегиба и промежутки выпуклости, вогнутости.

10 Сводная таблица.

Интеграл

Основные формулы

Совокупность всех первообразных функции 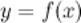, определенных на заданном промежутке, называется неопределенным интегралом от функции 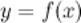и обозначается символом .

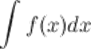То есть

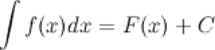
Знак 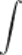называется интегралом, 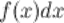- подынтегральным выражением, 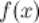- подынтегральной функцией, а 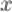- переменной интегрирования.

Операция нахождения первообразной или неопределенного интеграла от функции 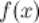называется интегрированием функции .

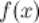Методы интегрирования

· Разложение

· Введение нового аргумента

· Интегрирование дробно-рациональных функций

48. Определённый интеграл — это форма ограниченная слева и справа прямыми а и b снизу осью ОХ сверху графиком функции f(x)

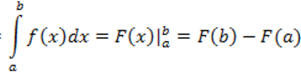
49. Криволинейные трапеции - называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a;b] функции f, осью Ox и прямыми x = a и x = b.

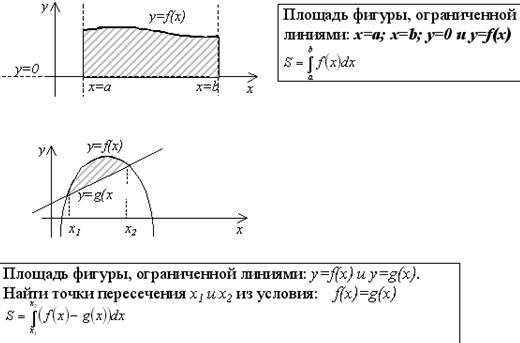
50. Вычисление площадей

.

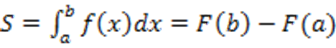Найти площадь фигуры, ограниченной линиями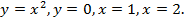

Вот искомая площадь:

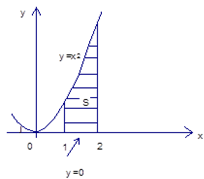
Вот формула: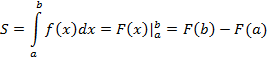

Пределы интегрирования .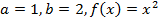

= .

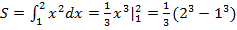Вычислили площадь криволинейной фигуры. Ответ:

Матрица

Матрица - это таблица данных, которая берется в круглые скобки.

Квадратная матрица

Квадратной матрицей называется матрица, у которой количество строк равно количеству столбцов (размера n×n), число n называется порядком матрицы.

Диагональная матрица

Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.

4. Матричная строка, столбец –

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов задает размер матрицы.

Количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

Единичная матрица

Единичной матрицей называется диагональная матрица, диагональные элементы которой равны 1.

6. Равные матрицы - Матрицы называются равными, если у них одинаковое число строк и столбцов и все соответствующие элементы совпадают.

Сложение матрицы

Сложение матриц (сумма матриц) A + B есть операция вычисления матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен:

сij = aij + bij

Умножение матриц

Произведением матрицы на матрицу называется матрица такая, что элемент матрицы , стоящий в -ой строке и -ом столбце, т.е. элемент , равен сумме произведений элементов -ой строки матрицы на соответствующие элементы -ого столбца матрицы .

Замечание

Умножать матрицы можно тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.

Умножение на число

Свойства умножения матрицы на число

1 · A = A

0 · A = Θ, где Θ - нулевая матрица

k · (A + B) = k · A + k · B

(k + n) · A = k · A + n · A

(k · n) · A = k · (n · A)

Найти произведение матрицы A = ( 4 2 ) и числа 5.

( 9 0 )

Решение:

5·A= 5· ( 4 2 ) = ( 5·4 5·2 ) = ( 20 10 )

( 9 0 ) ( 5·9 5·0 ) ( 45 0 )

Транспонированная матрица

Транспонирование матрицы - это операция над матрицей, при которой ее строки и столбцы меняются местами:

aTij = aji

A=					.

Решение:

AT=

Обратная матрица

Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице E:

A·A-1 = A-1·A = E

Свойства обратной матрицы:

1

2

3

4

Обратная матрица существует только для квадратных матриц с не равными нулю определителями.

12. Определители

A = ( 5 7 )

-4 1

Решение:

det(A) = (5 7)

(-4 1 ) = 5·1 - 7·(-4) = 5 + 28 = 33

Порядка

Го порядка

A = ( 5 7)

(-4 1)

Решение:

det(A) = (5 7)

(-4 1 ) = 5·1 - 7·(-4) = 5 + 28 = 33

Го порядка

∆ =

a11 a12 a13 a21 a22 a23 a31 a32 a33

=

= a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ - a₁₃·a₂₂·a₃₁ - a₁₁·a₂₃·a₃₂ - a₁₂·a₂₁·a₃₃

Линейные уравнения

из первого уравнения выразим:

Полученное выражение подставляем во второе уравнение:

Раскрываем скобки, приводим подобные слагаемые и находим значение :

Далее вспоминаем про то, от чего плясали:

Значение нам уже известно, осталось найти:

Ответ:

Векторы

Вектор это направляющий отрезок для которого указано какой из его концов является началом, а какой концом

16. Нулевой вектор – если начало и конец вектора совпадают

17. Длина вектора – расстояние между его началом и концом

18. Коллинеарные векторы – два ненулевых вектора, если они лежат на одной прямой или на параллельных прямых

19. Равные векторы – векторы которые сонаправленны и их длины равны