Элементы математики Свойства операций и отношений.
Элементы математики Свойства операций и отношений.
| Элементы: | Числовая алгебра | Право |
| 1. система объектов | Числа | Человек, государство, собственность, ... |
| 2. отношения между объектами | >, <, =, ... | родства, гражданство, к собственности (собственник, владелец,...), ... |
| 3. операции над объектами | + – */ ... | купли-продажи,... |
Часто абстрактные объекты в математике обозначаются именами. Например, в геометрии точки обозначаются прописными латинскими буквами A, B, C,...; имена отрезков образуются из имен концов отрезков – AB, CD,...., числовые значения длин отрезков представляются строчными латинскими буквами – a, b, c,... В числовой алгебре числа также могут заменяться именами: Вес = Рост – 100, a2 + b2 = c2, y < x2. Имена могут содержать и цифры, например, индексы: A1, x12..
В математике операции могут удовлетворять свойствам (на примере сложения и умножения чисел, для абстрактных сложения и умножения эти операции могут и называться не так):
a + b = b + a коммутативность
a(bc) = (ab)c ассоциативность
a(b + c) = ab + ac дистрибутивность (двух операций).
В числовой алгебре некоммутативными являются операции «/» и «–», они же не ассоциативны.
Отношения между объектами также могут обладать определенными свойствами.
Из a ▪ b и b ▪ c следует a ▪ c свойство транзитивности.
Например, в числовой алгебре:
из a < b и b < c следует a < c;
из a = b и b = c следует a = c
Свойство справедливо не для всех отношений. Например, отношение «является противоположным» не транзитивно. На множестве людей отношения «старше чем», «выше» обладают свойством транзитивности, а «является отцом» – нет.
Элементы теории множеств.
Под множеством мы будем понимать такой набор, группу, коллекцию элементов, обладающих каким-либо общим для них всех свойством или признаком.
Множества обозначим А, В, С…, а элементы множеств а, b, с…, используя латинский алфавит.
Можно сделать такую запись определения множества:
 , где
, где
“  ” – принадлежит;
” – принадлежит;
“=>“ – следовательно;
“ø” – пустое множество, т.е. не содержащее ни одного элемента.
Два множества будем называть равными, если они состоят из одних и тех же элементов
Например:

Если любой элемент из множества А принадлежит и множеству В, то говорят, что множество А включено в множество В, или множество А является подмножеством множества В, или А является частью В, т.е. если  , то
, то  , где “С” знак подмножества или включения.
, где “С” знак подмножества или включения.
Графически это выглядит так (рис.1):

(рис.1)
Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.

Рассмотрим операции над множествами и их графическую иллюстрацию (рис.2).
Объединением множеств А и В называется множество С, образованное всеми элементами, которые принадлежат хотя бы одному из множеств А или В. Слова “или” ключевое в понимании элементов входящих в объединение множеств.
Это определение можно записать с помощью обозначений:
А υ В, где 
где “ υ ” – знак объединения,
“ / ” – заменяет слова ”таких что“

(рис.2)
Пресечение двух множеств А и В называется множество С, образованное всеми элементами, которые принадлежат и множеству А, и множеству В. Здесь уже ключевое слово “и”. Запишем коротко:
А ∩ В = С, где 
“∩“ – знак пересечения. (рис.3)

(рис.3)
Обозначим буквой Е основное или универсальное множество, где  A С Е (“
A С Е (“  ”- любо число), т.е. А
”- любо число), т.е. А  Е = Е; А
Е = Е; А  Е =А
Е =А
Множество всех элементов универсального множества Е, не принадлежащих множеству А называется дополнением множества А до Е и обозначается ĀЕили Ā (рис.4)
 Е
Е
(рис.4)
Примерами для понимания этих понятий являются свойства:
_
А  Ā=Е Ø = Е Е Ā=Ā
Ā=Е Ø = Е Е Ā=Ā
_
А ∩ Ā= Ø Ē = Ø (Ā)=А
Свойства дополнения имеют свойства двойственности:
________ _ _
А  В = А∩В
В = А∩В
________ _ _
А  В = АUВ
В = АUВ
Введем еще одно понятие – это мощность множества.
Для конечного множества А через m (A) обозначим число элементов в множестве А.
Из определение следуют свойства:
m (A) + m (Ā) = m (E)
А = В => m(A) = m(B)
Для любых конечных множеств справедливы так же утверждения:
m (A  B) =m (A) + m (В) – m (А∩В)
B) =m (A) + m (В) – m (А∩В)
m (A∩B) = m (A) + m (В) – m (А  В)
В)
m (A  B
B  C) = m (A) + m (В) + m (С)– m (А∩В) - m (А∩С) – m (В∩С) – m (А∩В∩С).
C) = m (A) + m (В) + m (С)– m (А∩В) - m (А∩С) – m (В∩С) – m (А∩В∩С).
Объекты теории вероятностей
Случайное событие – всякий факт, который может произойти или не произойти в результате случайного явления.
Случайная величина – количественное проявление случайного явления, принимает различные значения.
Классификация событий
Все наблюдаемые при определенных условиях события можно разделить на следующие виды:
1) Достоверное – обязательно произойдет при определенных условиях. Например, выпадение какого-то очка при бросании кубика;
2) Невозможное – никогда не произойдет при определенных условиях. Например, выпадение 8 очков при однократном бросании одного кубика.
3) Случайное – может произойти или не произойти. Именно такие события изучает теория вероятности. Обозначается буквами латинского алфавита: А, В, С и т.п.
4) Несовместные – когда два события А и В одновременно не могут произойти. Например, А – выпадение «орла», В – выпадение «решки». Аналогия с не пересекающимися множествами:
| А |
| В |
5) Совместные – когда два события А и В протекают одновременно. Например, при бросании 2-х кубиков выпадение четных очков. Аналогия с пересекающимися множествами.
| А |
| В |
6) Независимые – наступление события А не влияет на наступление события В. Например, стрельба 2-х человек по мишени: промах одного не влияет (не зависит) на результат другого.
7) Зависимые – наступление или не наступление события А влияет на возможность наступления события В. Например, А – вытаскивание из колоды бубновой карты, В – вытаскивание затем бубнового туза.
8) Элементарное (простое) – событие, содержащее только один исход, не разложимое на другие события. Например,
испытание – стрельба по мишени
случайное событие – выбить не менее 7 очков – содержит 4 исхода, значит это не элементарное событие
случайное событие – выбить 10 очков – элементарное.
Совокупность всех исходов испытания называют пространством элементарных событий (исходов).
9) Противоположное событие – все остальные случаи, кроме рассматриваемого события.
Вероятность события.
На множестве случайных событий вводится числовая мера p, которая для события A характеризует степень возможности его наступления – вероятность и имеет тем большее значение, чем вероятнее событие.
Таким образом, вероятность события А, обозначаемая p (A) – это числовая мера возможности наступления случайного события.
Курсант стреляет 10 раз. Какова вероятность, что попадет 3 раза? – 3/10, т.е. 0,3.
В математике вероятность любого события находится всегда в интервале (т.е. для вероятности введено соглашение):
0 £ p (A) £ 1
События, для которых p (A) = 0 называются невозможными (не могут наступить); События, для которых p (A) = 1 называются достоверными (достоверно извест
Отношения между событиями
Отношения между событиями соответствуют рассмотренной классификации событий.
Дополним рассмотрение зависимых событий, т.е. когда вероятность события «зависит» от наступления другого события.
Шарики: 1 б + 2 ч. Два раза вытаскивают шарик. Какова вероятность каждый раз вытащить белый? Обозначим A – в первый раз белый, B – во второй раз белый. P(A) = P(B) = 1/3 (см. классический подход к определению вероятностей). А какова вероятность будет для второго раза, если известно, что в первый вытащен белый (наступило событие A) или вытащен черный (событие Ā)?
P (B|A) = 0. Запись читается: вероятность события B при условии, что наступило событие A, поэтому такую вероятность называют условной.
P (B|Ā) = 1/2
События A, B называются независимыми, если вероятность события B не зависит от того, произошло событие A или нет: P (B|A) = P (B). В противном случае события зависимы.
но об их наступлении).
Формула полной вероятности.
| H3 H1 A H2 |
Для любого события A будет справедливо разложение (см. рис. – A наступает всегда ровно с одним из Hi): A = H1A + H2,A +... + Hn A. Применяя аксиомы теории вероятностей, получим формулу полной вероятности:
p(A) = p(H1)p(A|H1) + p(H2) p(A|H2)+... + p(Hn)p(A|Hn)
p(H1)-вероятность одной из корзинок
p(A|H1)- вероятность вытянуть из корзинки H1 необходимый элемент
Примеры
Задача 1: Имеется 3 корзины, выбираем случайно одну, из которой вытаскиваем шарик. Определить вероятность того, что он окажется белым.
1-я: 3 б + 2 ч
2-я: 1 б + 4 ч
3-я: 2 б + 3 ч
Обозначим события H1 - выбрана 1-я корзина, H2 - 2-я, H3 - 3-я. Будем считать, что все события равновероятны (p(Hi) = 1/3).
p(б) = p(H1)p(б|H1) + p(H2) p(б|H2)+p(H3)p(б|H3) =1/3 3/5 + 1/3 1/5 + 1/3 2/5 = 6/15 = 2/5
Задача 2: Имеется корзина: 2 б + 3 ч. Игроки тащат по очереди. Сравнить вероятности вытаскивания белого у первого и второго игроков.
У первого p(б) = 2/5.
Второму может достаться для вытаскивания корзина 1 б + 3 ч (событие H1) или 2 б + 2 ч (событие H2). Первое событие происходит когда первый вытащит б, значит, p(H1) = 2/5, аналогично p(H2) = 3/5. Для второго:
p(б) = p(H1)p(б|H1) + p(H2) p(б|H2) = 2/5 1/4 + 3/5 2/4 = 8/20 = 2/5
Вероятности совпадают. Аналогично можно показать, что шансы всех участников равны.
Задача 3: Имеются корзины: 2 б + 3 ч и 1 б + 3 ч. Из второй в первую перекладывается случайно выбранный шарик. Определить вероятность того, что после этого из первой будет выбран белый.
p(б) = p(H1)p(б|H1) + p(H2) p(б|H2) = 1/4 * 3/6 + 3/4 * 2/6 = 9/24 = 3/8
9.Формула гипотез (Байеса).
Другое название – формула гипотез. Обратная задача: известно, что наступило некоторое событие, необходимо оценить вероятность различных гипотез при этом условии.
Часто существует несколько альтернативных гипотез из которых верна ровно одна. В результате эксперимента происходит событие A. Это может повлиять на оценку возможности гипотез. Например, от некоторых (несовместных с A) можно будет вообще отказаться.
Используя соотношение для любых событий Hk и A: p(Hk A) = p(Hk) p(A| Hk) = p(A) p(Hk |A), получим:
p(Hk |A) = p(Hk) p(A| Hk) / p(A)
Иногда p(A) известна, а в некоторых случаях ее можно получить по формуле полной вероятности.
Задача 1: В условиях задачи 1 на полную вероятность. Вытащили белый шар. Определить при этом вероятность того, что вытащили его из k-ой корзины (p(б) = 2/5 по формуле полной вероятности уже получена).
p(H1 |б) = p(H1) p(б| H1) / p(б) = 1/3 ´ 3/5 / 2/5 = 3/6 = 1/2
p(H2 |б) = p(H2) p(б| H2) / p(б) = 1/3 ´ 1/5 / 2/5 = 1/6
p(H3 |б) = p(H3) p(б| H3) / p(б) = 1/3 ´ 2/5 / 2/5 = 1/3
Задача 2: В условиях задачи 2 на полную вероятность. Второй игрок вытащил белый шарик. Определить при этом вероятности того, что первый вытащил белый и черный.
p(H1 |б) = p(H1) p(б| H1) / p(б) = 2/5 ´ 1/4 / 2/5 = 1/4
p(H2 |б) = p(H2) p(б| H2) / p(б) = 3/5 ´ 2/4 / 2/5 = 3/4
Отношения случайных величин
Две случайные величины x и y называются зависимыми, если распределение одной зависит от значения, которое принимает другая. Пример: зависимыми являются значения роста и веса случайных людей – интервалы значений случайной величины «вес» и средние веса для людей с ростом 160 см и ростом 210 см различаются.
Биномиальное распределение.
Случайное событие имеет вероятность p. Тогда вероятность того, что при n независимых испытаниях (вероятность одна и та же) оно наступит ровно m раз определяется:
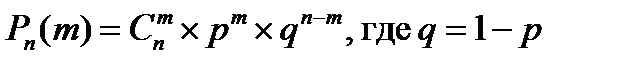
Случайная величина m – количество успехов в n независимых испытаниях имеет биномиальное распределение; p – вероятность успеха, q – неудачи. Биномиальным распределение называется потому, что вероятность является коэффициентами разложения бинома Ньютона: (p + q)n = pn(0) + pn(1) + ... + pn(n).
1. В городе каждый четвертый автомобиль – иномарка. Определить вероятность того, что из пяти встречных автомобилей три окажутся иномарками.
p = 1/4, q = 3/4, m = 3, n = 5.
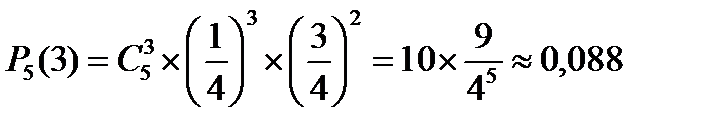
2. Вероятность при случайном блуждании по организации три раза подряд встретить женщину составляет 0,008. Определить долю мужчин в организации.
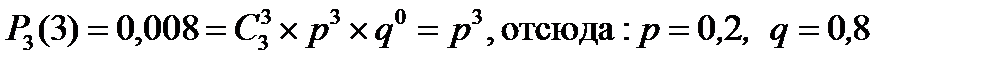
3. Шарики: 3 б + 2 ч. Вытаскиваем шар и кладем обратно (чтобы вероятность не менялась при следующем испытании – условие их независимости). Определить вероятность того, что из пяти попыток получим ровно 2 белых шара. Вероятность белого в каждой попытке одинакова p = 3/5; q = 2/5.
p5(2) = 10 ´ (3/5)2 ´ (2/5)3 = 720 / 55
4. Известна вероятность того, что встречный человек – мужчина p = 0,6. Определить вероятность того, что из десяти встреченных людей трое будут мужчинами.
p10(3) = (10!/(3! 7!)) ´ 0,63 ´ 0,47
5. Определить вероятность того, что событие из n попыток наступает хотя бы один раз. Заметим, что pn(0) + pn(1) + ... + pn(n) = 1 (полная группа событий). Отсюда:
p(событие наступает от одного раза) = pn(1) + ... + pn(n)= 1 – pn(0)= 1– qn
Выборочный метод
Генеральная совокупность – множество, подвергающееся изучению.
Выборочная совокупность (выборка) – подмножество генеральной совокупности, которое отбирается для наблюдения.
Объем выборки – количество элементов, входящих в нее.
Репрезентативность – способность выборки представлять свойства генеральной совокупности.
Ошибка репрезентативности – ошибка, возникающая потому, что выборка является только частью генеральной совокупности. Обстоятельства, определяющие величину ошибки репрезентативности:
1) способ формирования выборочной совокупности;
2) разброс изучаемого свойства в генеральной совокупности;
3) объем выборки.
Статистика – результат любой обработки выборки. Например, среднее значение, минимальное, размах.
Выборочный метод – получение свойств выборки и распространение их на всю генеральную совокупность.
Выборочные мода, медиана.
Медиана определяется таким образом, чтобы в выборке меньше ее и больше было одинаковое число значений. Для ее получения строится вариационный ряд и изучается его среднее положение:
2 3 5 910 20 100 для нечетного числа значений Me = 9
2 2 4 5 610 20 100 для четного числа значений Me = (5 + 6) /2 = 5,5.
Мода для выборки – наиболее часто встречающееся в выборке значение.
Например, для выборки x = 2, 5, 5, 3, 2, 3, 2, 1 Mo = 2
Для ряда распределения:
| X | 5 | 6 | |
| F | 8 | 4 | 4 |
Mo = 3, Me = 4
Для интервального ряда точка моды для интервала с наибольшей частотой определяется сложнее:
| X | x1 – x2 | x2 – x3 | x3 – x4 |
| F | f1 | f2 | f3 |
| f2 | ||||
| f1 | ||||
| f3 | ||||
| Mo | ||||
| x1 | x2 | x3 | x4 | |
 --+--------
--+--------
| X | 0 – 8 | 8 –16 | 16 –24 |
| F | 3 | 9 | 7 |
Mo = 8 + 8 / (1 + 2/6) = 14
| X | 0 – 5 | 5 –10 | 10 –15 |
| F | 2 | 5 | 3 |
| x | 5 – 10 | 10 –15 | 15 –20 |
| f | 5 | 20 | 10 |
Mo = 8
Mo = 13
Коэффициент корреляции
Для корреляционной связи двух величин существует оценка ее величины – коэффициент корреляции.
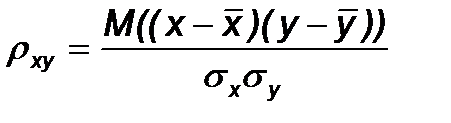
Свойства коэффициента корреляции:
1) для всех случаев значения находятся в интервале [–1,1];
2) для независимых величин равен нулю (обратное не обязательно верно!);
3) для связанных линейным соотношением y = kx + b он равен 1 или –1.
О силе связи судят по абсолютному значению коэффициента корреляции – чем оно больше, тем связь сильнее.
Элементы теории графов.
Оптимизация – поиск наилучшего по какому-либо критерию решения из возможных.
В качестве узла отмечают начало работы;
дуги – процесс ее выполнения. Узлов должно быть столько, сколько имеется работ; дуг – ровно столько, сколько чисел указано в колонке «работа». Дуги соединяют связанные работы: предварительная работа начинается, идет и только после ее окончания наступает зависимая работа. Числа на дугах соответствуют времени работ.
26. Задача определения пропускной способности сети.
Уже первое рассмотрение сети позволяет сделать вывод, что из узла (1) – источника не может вытекать поток более чем 8 + 2 = 10, а в узел (4) - сток не может втекать поток более чем 6 + 1 = 7, ведь потоку приходится проходить именно по дугам с такими пропускными способностями. Понятно, что поток не будет превышать min (10,7) = 7.
разрез сети – любое множество дуг, исключение которых отделяет источник от стока и не дает ресурсу перемещаться от первого ко второму.
Задача решается на основе теоремы о максимальном потоке:
Максимальный поток = минимальному разрезу.
Среди всех разрезов ищется с минимальной суммой, эта сумма и определяет пропускную способность всей сети.
На рисунке примера минимальным разрезом будет {(1,2),(3,4)}. Сумма пропускных способностей его 2+1=3 – самая маленькая, значит, и максимальный поток через данную сеть будет иметь значение 3.
27. Задача сетевого планирования.
Для комплекса работ, о каждой из которых известны время ее выполнения и перечень работ, которые должны быть завершены до ее начала, определить:
1). время начала каждой из работ;
2). время окончания всего комплекса.
Рассмотрим пример:
| Работа | Время выполнения | Работы, которые должны быть выполнены предварительно |
| 1. | ||
| 2. | ||
| 3. | ||
| 4. | 1, 2 | |
| 5. | 3, 4 |
Вводятся две фиктивные работы: «Начало» и «Конец» работ, и соединяются со всеми источниками и стоками соответственно. Фиктивные работы не требуют времени выполнения, их иногда называют событиями.
Алгоритм и его свойства.
Алгоритм – множество действий, связанных последовательностью выполнения. Может быть представлен в различной форме, главное, чтобы были отражены действия и связи следования. Например, может быть представлен в виде описания на языке (в том числе на алгоритмическом – специальном языке программирования). Иногда алгоритм представляется графически – в виде графа (блок-схемы). При этом узлы, описывающие действия, обозначаются с учетом специализации действий. Например, действие, заключающееся в проверке условия, обозначается ромбиком; в этом случае из него должны выходить две связи следования – в случае положительного и отрицательного результатов проверки. Обычное действие обозначается прямоугольником.
Свойства алгоритма: понятность для исполнителя, простота, правильность, число действий, число шагов (некоторые действия могут выполняться многократно), устойчивость (то есть насколько он работает правильно для различных данных), универсальность (насколько широко применим), скорость работы, точность (для приближенных алгоритмов), тип (по структуре – циклический, линейный,...).
Виды систем с управлением.
В общем случае для реализации в кибернетической системе основных функций управления необходимо включать в ее состав:
УО – управляющий объект;
ОУ – объект управления;
КПС – каналы прямой связи;
КОС – каналы обратной связи.
| УО |
| ОУ |
Виды систем с управлением:
Программное управление. 2) Управление по состоянию.
1)
| УО |
| ОУ |
| УО |
| ОУ |
| УО |
| ОУ |
| УО |
| ОУ |
Понятие электронной подписи
Реквизит электронного документа, полученный в результате криптографического преобразования информации с использованием закрытого ключа подписи и позволяющий проверить отсутствие искажения информации в электронном документе с момента формирования подписи (целостность), принадлежность подписи владельцу сертификата ключа подписи (авторство), а в случае успешной проверки подтвердить факт подписания электронного документа (неотказуемость)
На основе симметричного и ассиметричного шифрования.
Элементы математики Свойства операций и отношений.
| Элементы: | Числовая алгебра | Право |
| 1. система объектов | Числа | Человек, государство, собственность, ... |
| 2. отношения между объектами | >, <, =, ... | родства, гражданство, к собственности (собственник, владелец,...), ... |
| 3. операции над объектами | + – */ ... | купли-продажи,... |
Часто абстрактные объекты в математике обозначаются именами. Например, в геометрии точки обозначаются прописными латинскими буквами A, B, C,...; имена отрезков образуются из имен концов отрезков – AB, CD,...., числовые значения длин отрезков представляются строчными латинскими буквами – a, b, c,... В числовой алгебре числа также могут заменяться именами: Вес = Рост – 100, a2 + b2 = c2, y < x2. Имена могут содержать и цифры, например, индексы: A1, x12..
В математике операции могут удовлетворять свойствам (на примере сложения и умножения чисел, для абстрактных сложения и умножения эти операции могут и называться не так):
a + b = b + a коммутативность
a(bc) = (ab)c ассоциативность
a(b + c) = ab + ac дистрибутивность (двух операций).
В числовой алгебре некоммутативными являются операции «/» и «–», они же не ассоциативны.
Отношения между объектами также могут обладать определенными свойствами.
Из a ▪ b и b ▪ c следует a ▪ c свойство транзитивности.
Например, в числовой алгебре:
из a < b и b < c следует a < c;
из a = b и b = c следует a = c
Свойство справедливо не для всех отношений. Например, отношение «является противоположным» не транзитивно. На множестве людей отношения «старше чем», «выше» обладают свойством транзитивности, а «является отцом» – нет.
Элементы теории множеств.
Под множеством мы будем понимать такой набор, группу, коллекцию элементов, обладающих каким-либо общим для них всех свойством или признаком.
Множества обозначим А, В, С…, а элементы множеств а, b, с…, используя латинский алфавит.
Можно сделать такую запись определения множества:
 , где
, где
“  ” – принадлежит;
” – принадлежит;
“=>“ – следовательно;
“ø” – пустое множество, т.е. не содержащее ни одного элемента.
Два множества будем называть равными, если они состоят из одних и тех же элементов
Например:

Если любой элемент из множества А принадлежит и множеству В, то говорят, что множество А включено в множество В, или множество А является подмножеством множества В, или А является частью В, т.е. если  , то
, то  , где “С” знак подмножества или включения.
, где “С” знак подмножества или включения.
Графически это выглядит так (рис.1):

(рис.1)
Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.

Рассмотрим операции над множествами и их графическую иллюстрацию (рис.2).
Объединением множеств А и В называется множество С, образованное всеми элементами, которые принадлежат хотя бы одному из множеств А или В. Слова “или” ключевое в понимании элементов входящих в объединение множеств.
Это определение можно записать с помощью обозначений:
А υ В, где 
где “ υ ” – знак объединения,
“ / ” – заменяет слова ”таких что“

(рис.2)
Пресечение двух множеств А и В называется множество С, образованное всеми элементами, которые принадлежат и множеству А, и множеству В. Здесь уже ключевое слово “и”. Запишем коротко:
А ∩ В = С, где 
“∩“ – знак пересечения. (рис.3)

(рис.3)
Обозначим буквой Е основное или универсальное множество, где  A С Е (“
A С Е (“  ”- любо число), т.е. А
”- любо число), т.е. А  Е = Е; А
Е = Е; А  Е =А
Е =А
Множество всех элементов универсального множества Е, не принадлежащих множеству А называется дополнением множества А до Е и обозначается ĀЕили Ā (рис.4)
 Е
Е
(рис.4)
Примерами для понимания этих понятий являются свойства:
_
А  Ā=Е Ø = Е Е Ā=Ā
Ā=Е Ø = Е Е Ā=Ā
_
А ∩ Ā= Ø Ē = Ø (Ā)=А
Свойства дополнения имеют свойства двойственности:
________ _ _
А  В = А∩В
В = А∩В
________ _ _
А  В = АUВ
В = АUВ
Введем еще одно понятие – это мощность множества.
Для конечного множества А через m (A) обозначим число элементов в множестве А.
Из определение следуют свойства:
m (A) + m (Ā) = m (E)
А = В => m(A) = m(B)
Для любых конечных множеств справедливы так же утверждения:
m (A  B) =m (A) + m (В) – m (А∩В)
B) =m (A) + m (В) – m (А∩В)
m (A∩B) = m (A) + m (В) – m (А  В)
В)
m (A  B
B  C) = m (A) + m (В) + m (С)– m (А∩В) - m (А∩С) – m (В∩С) – m (А∩В∩С).
C) = m (A) + m (В) + m (С)– m (А∩В) - m (А∩С) – m (В∩С) – m (А∩В∩С).
