Внутренние усилия при изгибе

В инженерной практике часто применяются балки с поперечным сечением, имеющим вертикальную ось симметрии. Если внешняя нагрузка и реактивные усилия лежат в одной плоскости, которая совпадает с осью симметрии сечения, то балка будет изгибаться в той же плоскости (ось изгибаемого стержня не выходит из этой плоскости). Такой изгиб называютплоским (рис 7.4 а,б).

Далее будем рассматривать случаи, когда при плоском изгибе внешняя нагрузка перпендикулярна продольной оси балки. Поэтому в поперечном сечении балки возникают только поперечная сила и изгибающий момент , а продольная сила равна нулю. Такой изгиб называется поперечным.

Рис. 7.4 Плоский поперечный изгиб

Поперечная сила и изгибающий момент в данном поперечном сечении балки являются соответственно главным вектором и главным моментом относительно центра тяжести сечения внутренних сил, действующих в рассматриваемом сечении.

Условимся (рис. 7.5):

1) поперечную силу считать положительной, если она направлена так, что стремится повернуть элемент балки по ходу часовой стрелки;

2) изгибающий момент считать положительным, если он изгибает элемент балки выпуклостью вниз, вызывая растяжение нижних волокон.

а)
б) в)

г)

Рис. 7.5 Правило знаков для M и Q

Поперечная сила численно равна сумме проекций на нормаль к оси балки (на ось y) внутренних сил, а изгибающий момент – сумме моментов тех же сил относительно центра тяжести сечения.

Дифференциальные зависимости между M,Q и q.

Рассмотрим балку с внешней распределенной нагрузкой интенсивностью , направленной вниз вдоль положительной оси y (рис.7.6 а). Такую нагрузку будем считать положительной. Выделим из нее в произвольном месте элемент длиной (рис 7.6 б). Действие левой отброшенной части на элемент заменим поперечной силой и изгибающим моментом , а действие правой отброшенной части -

силой и моментом .

Рис 7.6 К выводу дифференциальных зависимостей

Здесь - приращение поперечной силы и изгибающего момента на элементе . На малом элементе интенсивность нагрузки можно считать постоянной. Составим уравнения равновесия:

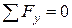(7.1)

(7.2)

Из уравнения (7.1) получим

(7.3)

Первая производная от поперечной силы по продольной координате xравна интенсивности распределенной нагрузки, взятой с обратным знаком.

Из уравнения (7.2), пренебрегая слагаемым как величиной второго порядка малости, получим

(7.4)

Первая производная от изгибающего момента по продольной координате xравна поперечной силе.

Зависимость (7.3) с учетом (7.4) можно записать в виде

(7.5)

Вторая производная от изгибающего момента по продольной координате xравна интенсивности распределенной нагрузки, взятой с обратным знаком .В дальнейшем индексы у будем опускать.