Раздел 1 множества и отношения

РАЗДЕЛ 1 МНОЖЕСТВА И ОТНОШЕНИЯ

Операции над множествами

Рассмотрим некоторые способы получения новых множеств из имеющихся. Эти способы называются операциями над множествами.

Пусть имеются два множества А и В.

Объединением (соединением, суммой) множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат А или В, т.е.

А È В = {x|x Î A или x Î B}

Здесь подразумевается не исключающий смысл слова «или». Т.о., по определению x Î AÈB тогда и только тогда, когда x есть элемент хотя бы одного из множеств А и В.

Например:

{1, 2, 3}È{1, 3, 4} = {1, 2, 3, 4}

Пересечением (произведением) множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат каждому из множеств А и В, т.е.

А Ç В = {x|(xÎA) Ç (xÎB)}

Например:

{1, 2, 3} Ç {2, 3, 4,} = {2, 3}

Множества, не имеющие общих элементов АÇВ=Æ, называют непересекающимися (расчлененными).

Разность А\В (или А – В) есть множество, состоящее из всех элементов А, не входящих в В, например, {1, 2, 3}\ {2, 3, 4} = {1}. Разность можно рассмотреть как относительное дополнение В до А. Если АÌU, то множество U\A называется абсолютным дополнением множества А и обозначается через 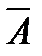. Оно содержит все элементы универсума U, кроме элементов множества А. Дополнение А определяется отрицанием свойства P(x) с помощью которого определяется А. Очевидно,

А\В = А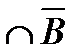

Дизъюнктивная сумма (симметрическая разность) А + В (или А Å В) есть множество всех элементов, принадлежащих или А, или В (но не обоим вместе). Например: {1, 2, 3} Å {2, 3, 4} = {1, 4}.

Дизъюнктивная сумма получается объединением элементов множеств за исключением тех, которые встречаются дважды.

Произведение множеств (декартово произведение) А´В есть множество всех упорядоченных пар элементов (а, b), из которых первый а принадлежит множеству А, а второй b – множеству В.

Например: А = {a₁, a₂, a₃, a₄} и B = {b₁, b₂}.

Тогда А ´ В = {(a₁, b₁), (a₁, b₂), (a₂, b₁), (a₂, b₂), (a₃, b₁), (a₃, b₂), (a₄, b₁), (a₄, b₂)}.

Порядок следования пар может быть любым, но расположение элементов в каждой паре определяется порядком следования перемножаемых множеств. Поэтому В ´ А ¹ А ´ В, если А ¹ В. Указанные операции над множествами обобщаются на любое их количество А₁, А₂, …, А_n. Так, в частности операция произведения множеств записывается

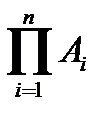= A₁ ´ A₂ ´ … ´ A_n.

В результате получаем множество упорядоченных совокупностей (a₁, a₂, …, a_n), для которых употребляется название: кортеж, последовательность, вектор или просто n-ка, часть для того, чтобы отразить строго определенный порядок следования элементов n-ки записывают <a₁, a₂, …, a_n>.

В частности, если A₁=A₂=…=A_n=A, декартово произведение называется n–кратным или декартовой n-й степенью и обозначается Аⁿ.

Операции над отношениями

Т.к. отношение – это множества, то над ними можно выполнять все теоретико-множественные операции как и над обычными множествами. Кроме этого для отношений существуют специфические операции: обращение (симметризация) и композиция.

Отношение, симметричное (обратное) некоторому отношению 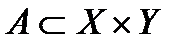, обозначается через 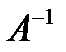и представляет собой подмножество множества 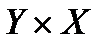, образованное теми парами 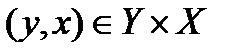, для которых 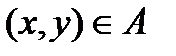. Переход от А к 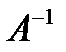осуществляется взаимной перестановкой координат местами каждой упорядоченной пары. Так, обратное отношение для «x есть делитель y» будет «y делится на x» и для приведенного примера выполняется множеством .

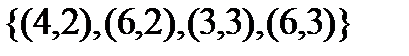При переходе от А к 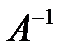область определения становится областью значений, и наоборот. Матрица обратного отношения получается транспонированием исходной матрицы. Граф обратного отношения находится из исходного графа заменой направлений всех дуг на противоположные.

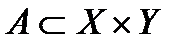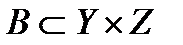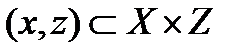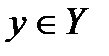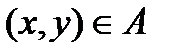Композиция отношений и есть отношение С, состоящее из всех тех пар , для которых существует такое , что и .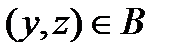

Сечение отношения С по x совпадает с сечением отношения B по подмножеству 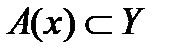, т.е. .

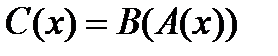Рассмотрим, например, два отношения: . .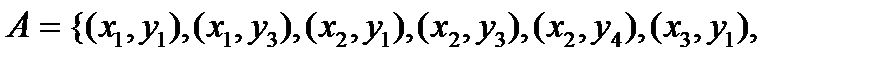

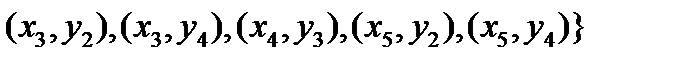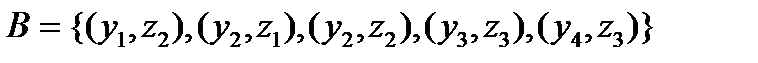Очевидно, 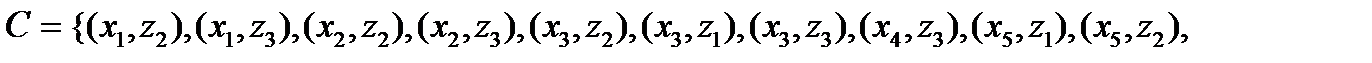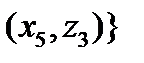. Сечение 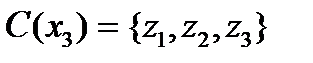. С другой стороны,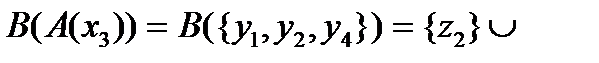

.

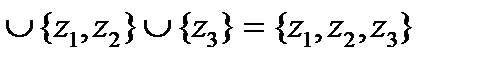Композицию С отношений А и B обычно записывают как 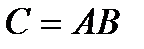(или 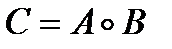), тогда .

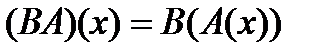Композиция отношений обладает ассоциативным законом 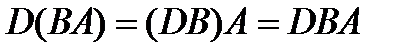, но не коммутативна 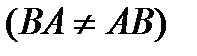. Можно показать , что 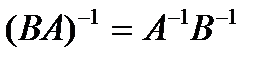. Композиция отношени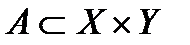й и 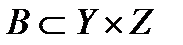наглядно представляется с помощью графов.

Прежде всего необходимо к графу отношения А добавить граф отношения В. Граф отношения 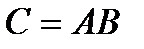получим, исключив вершины, соответствующие элементам множества Y. При исключении вершины 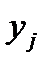каждый проходящий через нее путь от вершины x к вершине z заменяется одной дугой с тем же направлением. Параллельные ветви с одинаковыми направлениями соответствуют одинаковым парам в С и рассматриваются как одна ветвь.

Аналогично можно получить матрицу композиции 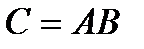как произведение матриц отношений A и B, которое выполняется по обычному правилу умножения прямоугольных матриц с последующей заменой отличного от нуля элемента результирующей матрицы единицей.

Свойства отношений

Пусть А – бинарное отношение в множестве X. Определим общие свойства таких отношений, которые должны выполняться для всех 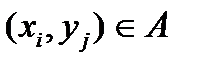. Говорят, что :

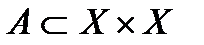Рефлексивно, если 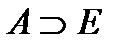(Е – тождественное отношение), т.е. оно всегда выполняется между объектом и им самим: 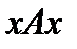. Этому отношению принадлежат все пары 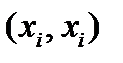, т.е. пары, в которых отношения «быть делителем на множестве N, т.к. каждое число из N является делителем самого себя. На графе свойство рефлексивности отображается петлей у каждой ветви.

Антирефлексивно, если 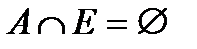, т.е. может выполняться только для несовпадающих объектов: из 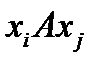следует .

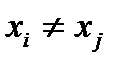Свойство симметричности, если 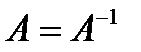, т.е. при выполнении соотношения 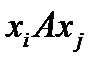выполняется и соотношение 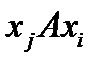(«быть родственником»).

Свойство асимметричности, если 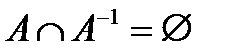, т.е. из двух соотношени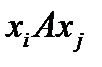й и 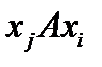по меньшей мере одно не выполняется; если отношение асимметрично, то оно и антирефлексно.

Свойство антисимметричности, если 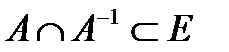, т.е. оба соотношения 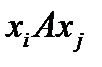и 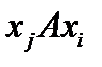выполняются одновременно только тогда, когда 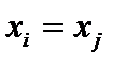(нестрогое неравенство 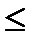; включение)

Свойство транзитивности, если 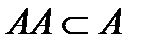, т.е. из 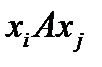и 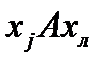(«быть делителем», «быть родственником»), т.е. если элемент x находясь в отношении с элементом y и элемент y находится в отношении A с элементом z, то элемент x находится в отношении A с элементом z. 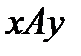и .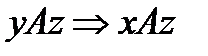

Для рефлексивного отношения все элементы матрицы на главной диагонали – единицы, а для антирефлексивного – нули. Симметричность отношения влечет и симметричность матрицы, асимметричность отношения – несимметричность матрицы с нулевыми элементами на главной диагонали, антисимметричность отношения – только несимметричность матриц. В матрице транзитивного отношения для каждой пары единичных элементов, один из которых расположен в i-м столбце и j-й строке, а другой в j-м столбце и k-й строке, обязательно существует единичный элемент, расположенный в клетке на пересечении i-го столбца и k-й строки.

РАЗДЕЛ 1 МНОЖЕСТВА И ОТНОШЕНИЯ