Классификация основных процессов и аппаратов химической технологии

Содержание

Условные обозначения. 3

Введение. 5

1. Общие положения. 6

1.1 Классификация основных процессов и аппаратов химической технологии. 7

1.2 Кинетические закономерности основных процессов химической технологии. 10

1.3 Общие принципы расчёта химических машин и аппаратов. 11

1.4 Применение метода моделирования для исследования и расчета ПАХТ. 13

1.5 Геометрическое и физическое подобие. 16

2. Гидромеханические процессы.. 20

2.1 Физические свойства жидкостей и газов. 20

2.2 Гидравлика. 23

2.2.1 Гидростатика. 23

2.2.2 Практическое приложение уравнения гидростатики. 26

2.3 Гидродинамика. 29

2.3.1 Основные характеристики движения жидкостей. 29

2.3.2 Распределение скоростей в движущемся потоке жидкости. 35

2.3.3 Дифференциальные уравнения движения Эйлера. 37

2.3.4 Дифференциальные уравнения движения Навье–Стокса. 38

2.3.5 Уравнение Бернулли. 39

2.3.6 Гидродинамическое подобие. 46

2.3.7 Гидравлические сопротивления в трубопроводах и каналах. 49

2.3.8 Движение тел в жидкостях. 51

2.3.9 Движение жидкостей через неподвижные пористые слои. 55

2.3.10 Гидродинамика псевдоожиженных слоев. 58

2.3.11 Гидродинамика двухфазных потоков. 61

2.4. Перемещение жидкостей (насосы) 69

2.4.1. Классификация и области применения насосов. 69

2.4.2. Параметры насосов. 73

2.4.3. Насосная установка. 75

2.4.4. Основное уравнение лопастных машин (уравнение Эйлера) 77

2.4.5. Характеристики центробежных насосов. 79

2.5. Процессы разделения неоднородных смесей. 81

2.5.1. Классификация неоднородных систем и способов их разделения. 81

2.5.2. Материальные балансы процессов разделения. 83

2.5.3 Осаждение. 84

2.6 Фильтрование. 92

2.6.1 Уравнения фильтрования. 92

2.6.2 Определение постоянных в уравнениях фильтрования. 95

2.6.3 Центробежное фильтрование. 96

2.7 Перемешивание в жидкой фазе. 98

2.7.1 Механические перемешивающие устройства. 98

2.7.2 Конструкции мешалок. 99

Библиографический список. 103

Условные обозначения

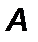–работа, Дж;

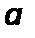– удельная поверхность зернистого слоя, м²/м³,

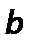–коэффициент температуропроводности, м²/с;

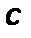–удельная теплоемкость вещества, Дж/(кг·с);

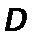–коэффициент диффузии, м/с²;

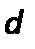– диаметр, м;

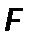–поверхность теплообмена, м²;

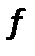–площадь поперечного сечения, м²;

g –ускорение свободного падения, м/с²;

H –напор насоса, высота, м;

h –высота, м;удельная энтальпия, Дж/кг;

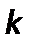–коэффициент скорости процесса;

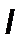–длина, м;

L –работа;

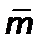–массовый расход, кг/с;

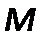–масса вещества, кг;

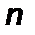–частота вращения, с^-1;

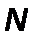–мощность;

Р –сила, Н;

р –гидростатическое давление, Н/м²;

Q –количество вещества, тепла ( тепловой поток), Дж;

q –удельныйтепловой поток, Дж/м²;

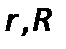–радиус, м;

Т – абсолютная температура, К;

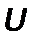–периметр, м;

–объем, м³;

v –удельный объем, м³/кг ;

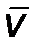–объемный расход, м³/с;

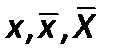–мольная, массовая, относительнаямассовая доля компонента жидкости в растворе;

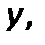
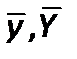–мольная, массовая, относительнаямассовая доля компонента газа в смеси;

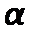– коэффициент теплоотдачи, Вт/(м²/К);

–коэффициент массоотдачи, кг/(м²·с·ед. движ. силы);

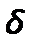– толщина стенки, пленки жидкости, пограничного слоя, зазор, м;

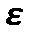– порозность зернистого слоя, относительная шероховатость поверхности;

φ –угол, химический потенциал;

η –КПД системы, установки;

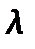– коэффициент теплопроводности, Вт/(м·К);

μ –динамический коэффициент вязкости, Па·с;

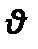–безразмерная температура;

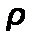– плотность вещества, кг/ м³;

–коэффициент поверхностного натяжения, Н/м;

τ – время, с;

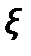–коэффициент местного сопротивления.

Введение

В связи со специфическими особенностями в системе материального производства химическая промышленность занимает особое место. Эти особенности обусловлены разнообразием и узкой специализацией применяемых машин и аппаратов, широким выбором источников сырья для производства одного и того же продукта, большой материалоемкостью, высоким энергопотреблением и степенью автоматизации производства и определяют высокую эффективность химической промышленности, способность быстро и гибко перестраиваться на производство новых видов продукции. Химическая, нефтехимическая и нефтеперерабатывающая промышленности оснащены самыми разнообразными машинами и аппаратами, стандартным, нестандартным и оборудованием специального назначения. В них обрабатывается сырье и целевые продукты различного агрегатного состояния, агрессивные и коррозионно-активные вещества, используются разнообразные виды энергии.

Развитие и техническое совершенствование химических и нефтехимических производств определяется значительным прогрессом в оформлении технологических процессов, появлением новых видов и конструкций оборудования, повышенными требованиями к его расчету и проектированию.

В процессе химического и нефтехимического производства сырье перерабатывается в целевой продукт. Для этого осуществляется ряд операций (стадий технологического процесса), включающих в себя подготовку сырья к его переводу в реакционноспособное состояние, химическое взаимодействие исходных компонентов (реагентов) и обработку полученной реакционной смеси. Для этих целей при аппаратурном оформлении того или иного технологического процесса помимо реакционных аппаратов используются различные механические процессы и аппараты для смешения, разделения, диспергирования сырья, гидромеханическое, тепловое, тепло- и массообменное оборудование.

Дисциплина «Процессы и аппараты химической технологии» базируется на фундаментальных законах физики и химии. Содержание разделов этой дисциплины во многом определяется спецификой производств региона, задачами подготовки специалистов широкого профиля, способных не только представлять сложные физико-химические процессы в виде уравнений, но и воплощать их в конкретном технологическом и аппаратурном оформлении, обеспечивающем строгие требования к качеству целевых продуктов, ресурсосбережению и экологической безопасности производств. При этом необходимо учитывать повышение значимости самостоятельного изучения предмета студентами в условиях возрастания объема программного материала при сохранении и даже сокращении числа учебных часов.

Общие положения

Совокупность тел, взаимодействующих между собой, представляет систему. Изменение состояния какой-либо системы, ее беспрерывное движение и развитие, происходящие в природе, производстве, лаборатории, обществе представляют собой процесс.

Нами будут рассматриваться процессы, создаваемые в определенных технологических целях.

Технология – наука о практическом применении законов физики, химии, биологии и других базисных наук для проведения технологических процессов. Эта наука возникла как самостоятельная отрасль знания в концеXVIII века в связи с ростом крупного машинного производства.

В технологии условно выделяют механическую и химическую технологии.

Механическая технология изучает процессы, в которых изменяются только физические свойства или форма перерабатываемых материалов.

Химическая технология представляет собой набор физических и химических процессов и средств, с помощью которых исходное сырье превращается в целевые продукты (в промежуточное сырье, продукты потребления).

Для осуществления процессов необходимы машины и аппараты, иными словами процесс должен иметь определенное аппаратурное оформление.

Устройство, созданное человеком и выполняющее механическое движение для преобразования энергии, материалов и информации с целью полной замены или облегчения физического и умственного труда человека, увеличения его производительности, называется машиной.

Машины, предназначенные для преобразования обрабатываемого предмета (продукта), состоящего в изменении его размеров, формы, свойств или состояния, называются технологическими. К ним относятся также и аппараты.

Под словом «аппарат» понимается любое устройство, в котором протекает технологический процесс. Чаще всего аппарат является сосудом, снабженным различными механическими приспособлениями. Однако некоторые из рассматриваемых в дисциплине устройств представляют собой типичные рабочие машины, например: центробежный экстрактор, дозатор, дробилку.

Машины и аппараты, различающиеся по своему технологическому назначению и конструктивному оформлению, состоят в основном из типовых деталей и узлов.

Характерной особенностьюмашин является наличие неподвижных и движущихся элементов, включающих в себя рабочие органы, валы, подшипники, корпуса (станины), привод и т.п.

Аппараты состоят, как правило, из неподвижных элементов: обечаек, крышек, опор, фланцев и др.

Технология производства самых разнообразных химических продуктовиматериалов состоит из ряда однотипных физических и физико-химических процессов, характеризуемых общими закономерностями.

Эти процессы в различных производствах проводятся в аналогичных по принципу действия машинах и аппаратах. Процессы и аппараты, общие для различных отраслей химической технологии, называют основными процессами и аппаратами.

Например, перегонка жидкостей (ректификация) – процесс разделения жидких смесей, основанный на различии температур кипения компонентов смеси при одинаковом давлении. Этот процесс применяется для разделения жидкого воздуха при получении азота, кислорода и других газов, разделения воды и азотной кислоты в производстве азотной кислоты, разделения воды и спирта, нефти, а также сложных смесей органических продуктов для получения дивинила в производстве синтетического каучука и т.п.

К числу основных аппаратов относятся тарельчатые и насадочные колонны, применяемые не только для проведения процессов ректификации, но и абсорбционных и экстракционных процессов, очистки газов от пыли и т.п.

Насосы, компрессоры, фильтры, центрифуги, теплообменники и сушилки также относятся к числу основных аппаратов и машин, которые в различных сочетаниях составляют типовое оборудование большинства химических производств.

Таким образом, в дисциплине «Процессы и аппараты химической технологии»(ПиАХТ) изучается теория основных процессов, принципы устройства и методы расчета аппаратов и машин, используемых для проведения химико-технологических процессов.

Анализ закономерностей протекания основных процессов и разработка обобщенных методов расчета аппаратов производится исходя из фундаментальных законов природы, физики, химии, термодинамики и других наук. Курс построен на основе выявления аналогии внешне разнородных процессов и аппаратов независимо от отрасли химической промышленности, в которой они используются.

В курсе ПиАХТ также изучаются закономерности перехода от лабораторных процессов к промышленным. Знание закономерностей перехода от одного масштаба к другому (от «стекла» к «железу») необходимо для проектирования большинства современных производственных процессов химической технологии. Химический процесс, изучаемый в пробирке, не всегда может быть воспроизведен с теми же показателями в крупном масштабе. Для осуществления процесса в промышленном реакторе помимо химической сущности процесса должны быть установлены его параметры в зависимости от конструкции аппарата, структуры потоков и режимов их движения, скорости переноса тепла и массы и др.

Совокупность влияния этих факторов определяет так называемую макрокинетику процесса, связанную с массовым движением макрочастиц – пузырей, капель, струй и т. п.

В науке о ПиАХТ изучается макрокинетика основных процессов химической технологии. При этом используются данные по микрокинетике, характеризуемой элементарными, независимо протекающими на молекулярном уровне процессами, такими, как теплопроводность, молекулярная диффузия и другими, которые рассматриваются в физике, физической химии, химической термодинамике и других науках.

Курс ПиАХТ является инженерной дисциплиной, представляющей собой важный раздел теоретических основ химической технологии. Этот курс является составной частью комплекса дисциплин, освещающих различные аспекты химической технологии как науки. К таким дисциплинам относятся курсы общей химической технологии и технологии конкретных отраслей химической промышленности.

Дисциплина ПиАХТ основывается на общих законах физики и химии и является теоретической основой химической технологии, позволяющей проанализировать и рассчитать процесс, найти его наиболее рациональные (наивыгоднейшие, оптимальные) параметры, а также разработать и рассчитать аппаратуру, необходимую для проведения этого процесса.

За время становления курса ПиАХТв него вошли четыре основные группы процессов: механические, гидромеханические, тепловые и массообменные. И при этом рассматриваются не только процессы, но и аппараты, в которых протекают эти процессы.

Гидромеханические процессы

Гидравлика

Гидромеханические процессы, связанные с перемещением жидкостей, сжатием и перемещением газов иногда называют гидравлическими по названию раздела гидромеханики – гидравлике, рассматривающей жидкости и газы как рабочие тела различных технических систем.

Гидравлика представляет собой науку, изучающую законы равновесия и механического движения жидкостей и разрабатывающую методы применения этих законов для различных прикладных задач.

Гидравликой рассматриваются вопросы покоя и движения жидкостей в двух разделах – гидростатике и гидродинамике. Гидростатика рассматривает законы равновесия в состоянии покоя, гидродинамика – законы движения жидкостей и газов.

Гидростатика

В гидростатике равновесие жидкостей рассматривается в состоянии относительного покоя, при котором в движущейся жидкости ее частицы не перемещаются друг относительно друга. Силы внутреннего трения отсутствуют, поэтому жидкость можно считать идеальной.

В состоянии покоя форма объема жидкости не изменяется и подобно твердому телу перемещается как единое целое.

Независимо от вида покоя на жидкость действуют силы тяжести и давления. В случае относительного покоя необходимо учитывать силу инерции переносного движения жидкости. Соотношение между силами, действующими на жидкость, которая находится в состоянии покоя, определяющему условия равновесия жидкости, выражается дифференциальными уравнениями равновесия Эйлера.

Дифференциальные уравнения равновесия Эйлера. В объеме жидкости, находящейся в покое (рис. 2.2), выделим элементарный параллелепипед объемом dVc ребрами dx,dy, dz, расположенными параллельно осям координатx, y, иz .

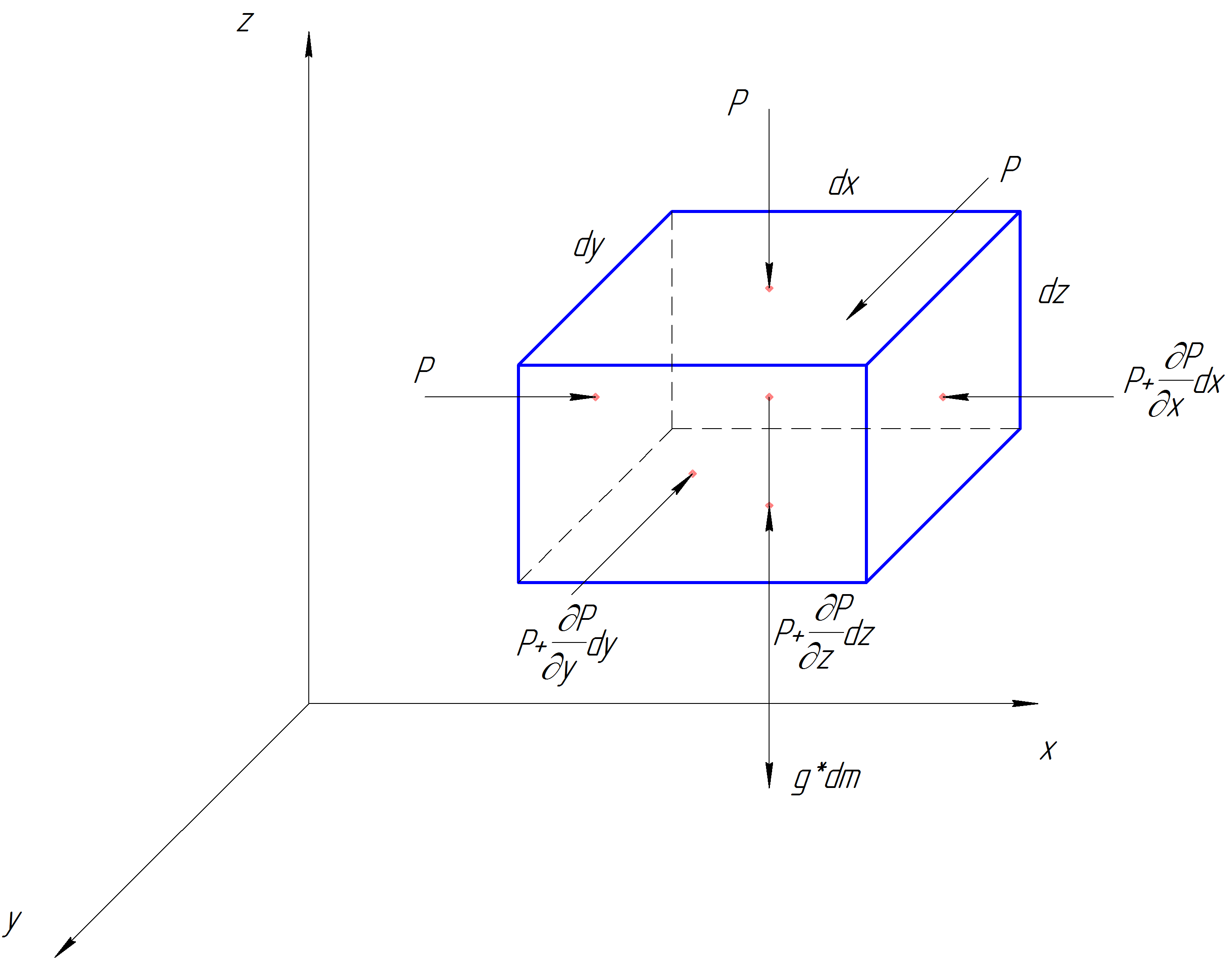
Рис. 2.2. К выводу дифференциальных уравнений равновесия Эйлера

Согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю.

Запишем уравнения равновесия для осей :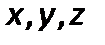

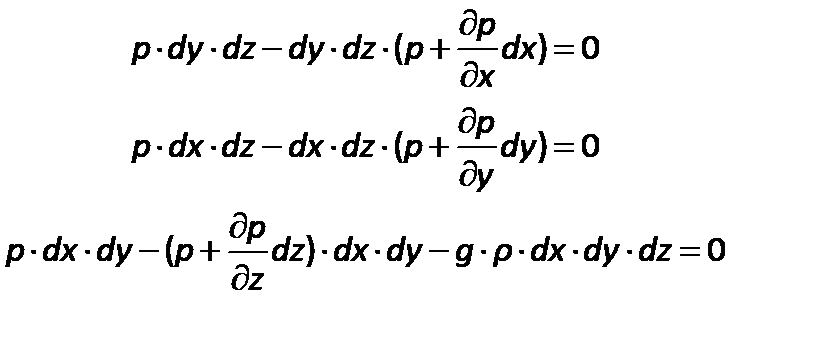(2.13)

Раскрыв скобки, получим:

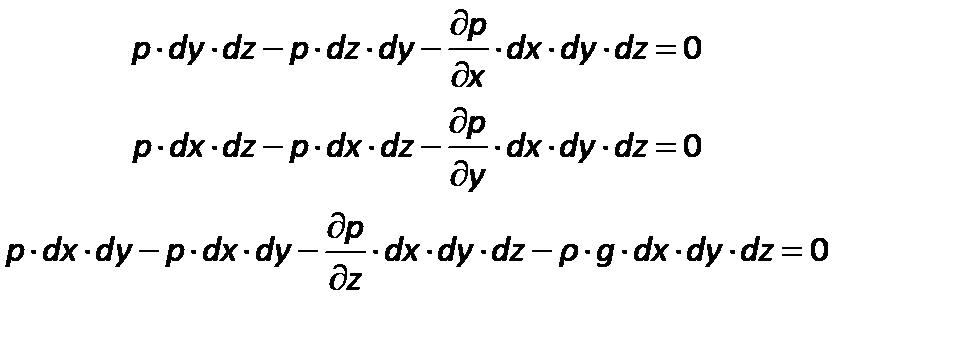(2.14)

После преобразований получим дифференциальные уравнения Эйлера:

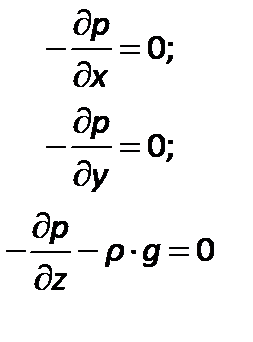(2.15)

Для нахождения закона распределения давления во всем объеме покоящейся жидкости p=f(x, y, z) необходимо проинтегрировать систему уравнений.

Гидростатические машины

На использовании основного уравнения гидростатики основана работа гидравлических прессов, домкратов, гидроцилиндров и др. Если в гидропрессе
(рис. 2.5) приложить небольшое усилие к поршню 1, перемещаемому в цилиндре меньшего диаметра 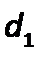, и создать давление на поршень, то, согласно закону Паскаля, такое же давление будет приходиться на поршень 2 в цилиндре с большим диаметром 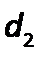, при этом сила давления на поршень 1 составит

,

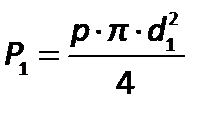а сила давления на поршень 2

.

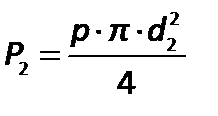В результате поршень в цилиндре большего диаметра передает силу давления во столько раз большую, чем сила, приложенная к поршню в цилиндре меньшего диаметра, насколько поперечное сечение цилиндра 2 больше, чем цилиндра 1, т.е.:

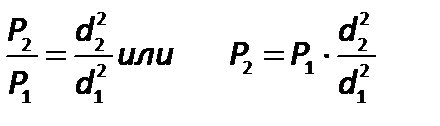(2.21)

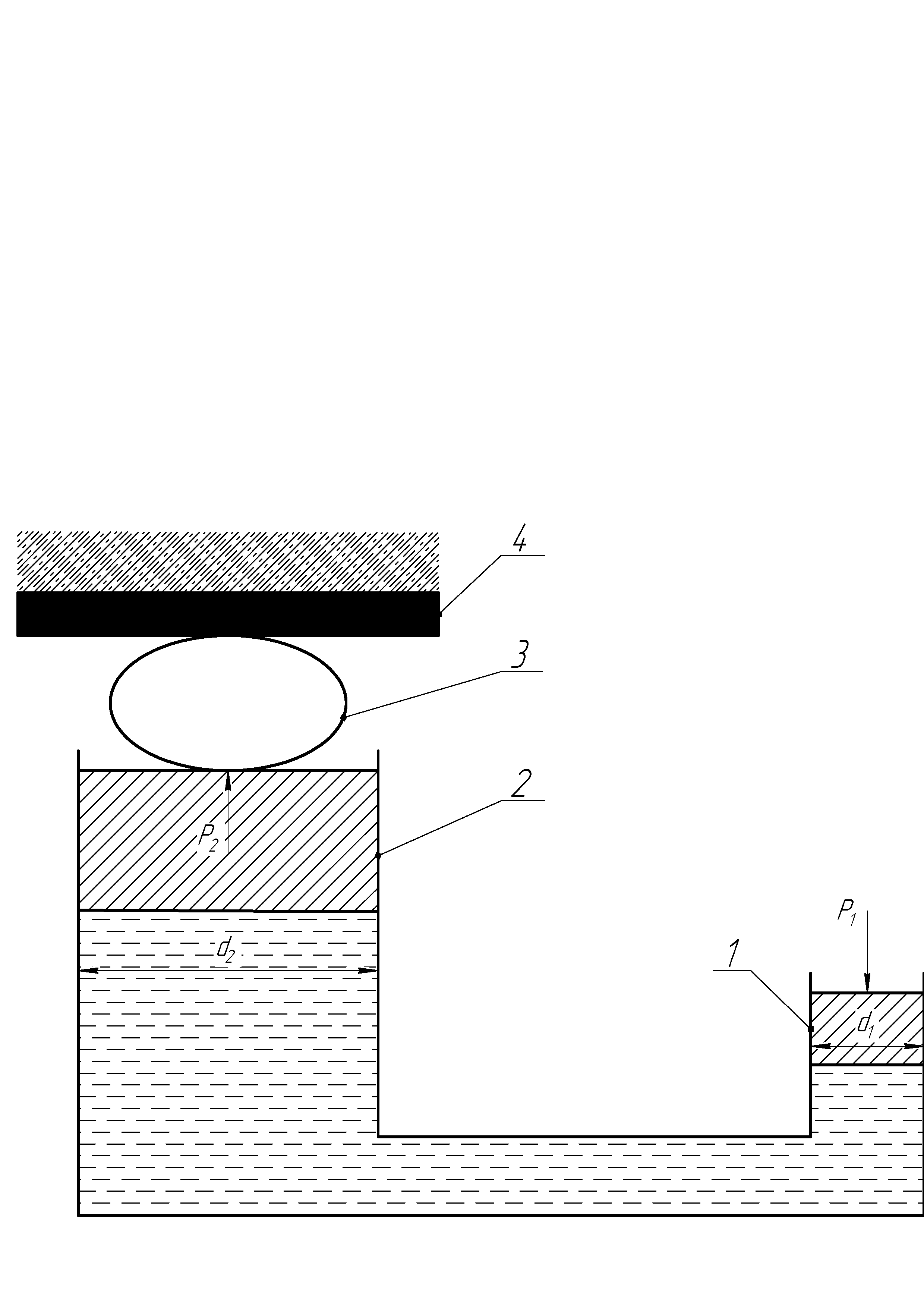
Рис. 2.5. Схема гидравлического пресса:
1, 2 – цилиндры пресса;3 – изделие; 4 – неподвижная плита

Гидродинамика

Движущей силой при течении жидкости является разность давлений, которая создается с помощью насосов или компрессоров, либо вследствие разности уровней или плотностей жидкости.

Знание законов гидродинамики позволяет находить Δp, необходимое для перемещения заданного количества жидкости с требуемой скоростью, а значит и расход энергии на это перемещение. И наоборот, определить скорость и расход жидкости при заданном Δp.

Различают внутреннюю, внешнюю и смешанную задачи гидродинамики.

К внутренней задаче гидродинамики относятся вопросы изучения закономерностей движения жидкости и газов внутри труб и каналов. Внешняя задача связана с изучением закономерностей обтекания жидкостями и газами различных тел (процессы осаждения, механического перемешивания и т.д.). Смешанная задача заключается в изучении движения жидкости и газов через зернистые и пористые слои твердых материалов. Жидкость в этом случае движется одновременно внутри каналов сложной формы и обтекает твердые частицы (процессы фильтрования, течения жидкостей и газов через насадки массообменных аппаратов, реакторов с твердым катализатором и т.п.).

Скорость и расход жидкости

Количество жидкости, протекающей через поперечное сечение потока в единицу времени, называется расходом жидкости.

Различают объемный (м³/с)и массовый (кг/с) расходы.

В разных точках поперечного сечения потока скорости частиц жидкости неодинаковы, поэтому в расчетах используют не истинные (локальные) скорости, а фиктивную среднюю скорость:

.

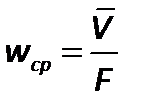Объемный расход жидкости равен – ,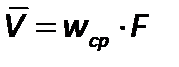

массовый расход – ,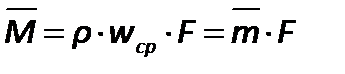

массовая скорость жидкости– .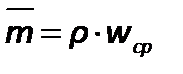

Режимы движения жидкостей

Характер движения жидкости зависит от скорости ее течения. Этот вопрос был решен в 1883 г. О. Рейнольдсом, который поставил простой убедительный опыт. Установка О. Рейнольдса показана на рис. 2.7. Характер движения жидкости устанавливается по степени размытости струйки подкрашенной жидкости, истекающей по трубке 2 из сосуда 1. В зависимости от высоты уровня жидкости в сосуде 1, устанавливалась та или иная скорость течения.

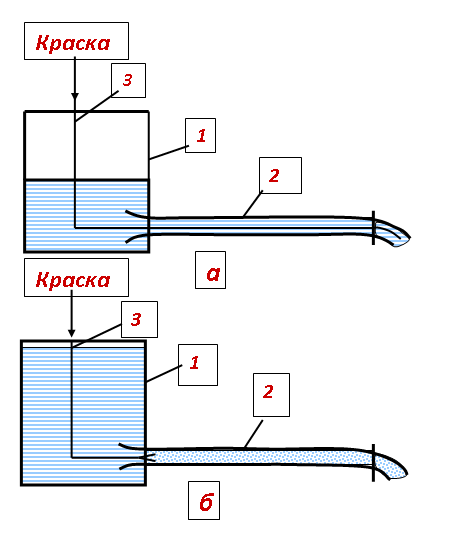
Рис. 2.7. Опыт Рейнольдса:

а – ламинарное движение; б – турбулентное движение

При малых скоростях течения струя окрашенной жидкости 3 не размывалась, что указывало на послойный характер движения жидкости. Такие течения были названы ламинарными.

При некоторойкритической скорости струйка размывалась по всему сечению, что свидетельствовало о вихревом характере перемешивания жидкости по всему сечению трубы 4. Такой режим течения был назван турбулентным. Рейнольдс показал, что переход от одного режима течения к другому соответствует определенному значению безразмерной величины:

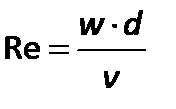(2.44)

где 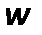–средняя скорость; 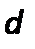–диаметр канала; –кинематический коэффициент вязкости жидкости.

Безразмерная переменная впоследствии был названа числом или критерием Рейнольдса.

Переход от ламинарного течения наступает при 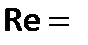2300.При 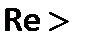2300 чаще всего наблюдается турбулентный режим течения. Однако при
2300 10000 режим течения неустойчиво турбулентный, или переходный.

Вышесказанное справедливо к стабилизированным изотермическим потокам в прямых трубах с малой шероховатостью стенок. Наличие различных возмущений, обусловленных шероховатостью стенок трубы, изменением скорости или направления течения потока, близость входа в трубу и т. п. могут существенно снизить значения критических чисел Рейнольдса.

Ламинарный режим

Распределение скоростей определяется режимом течения жидкости. При ламинарном режиме распределение может быть установлено законом Стокса:

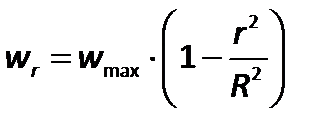(2.45)

представляющим параболическое распределение скоростей в сечении трубопровода,где –текущий радиус, отсчитываемый от оси трубопровода; –скорость на оси трубопровода.

Средняя скорость по сечению трубопровода связана с максимальной скоростью следующим соотношением:

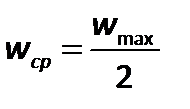(2.46)

Уравнение, определяющее объемный расход жидкости при ее ламинарном движении в круглой прямой трубе, носит название уравнения Пуазейля:

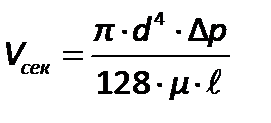(2.47)

Турбулентный режим

Турбулентный режимимеет наибольшее распространение в промышленной практике, характеризуется пульсационным движением частиц в продольном и поперечном направлениях по отношению к основному движению потока.

При турбулентном течении из-за хаотического движения частиц происходит выравнивание скоростей в основной массе потока и их распределение по сечению трубы характеризуется кривой, отличающейся по форме от параболы. При этом кривая имеет более широкую вершину (рис. 2.8).

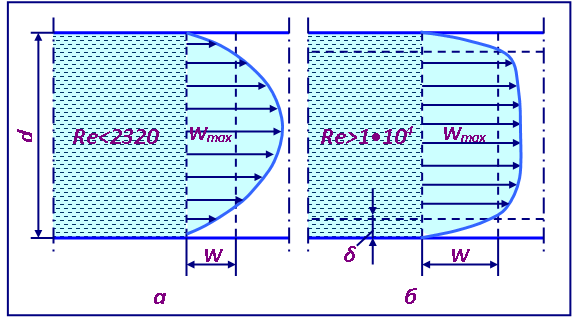
Рис. 2.8. Распределение скоростей при различных режимах движения:

а) ламинарный поток; б) турбулентный поток

В результате экспериментов установлено, что средняя скорость при турбулентном режиме не равна половине максимальной, как для ламинарного течения, а значительно больше этой величины, причем отношение 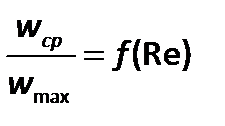. Например, при 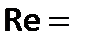10⁴скорость 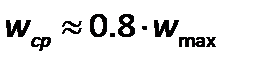, а при .

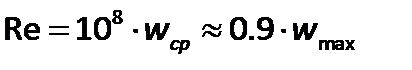В связи со сложным характером турбулентного движения не представляется возможным теоретически получить профиль распределения скоростей и значение 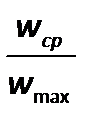. Кроме того, при турбулентномтечении профиль скоростей выражает распределение не истинных, а осредненных во времени скоростей.

В каждой точке турбулентного потока истинная скорость не остается постоянной во времени из-за хаотического движения частиц. Мгновенные значения скорости испытывают флуктуации, или нерегулярные пульсации, имеющие неустановившийся характер (рис. 2.9).

Истинную скорость измерить практически невозможно из-за хаотического перемещения частиц во всех направлениях. Скорости пульсируют около некоторой усредненной величины, превышая или становясь меньше ее.

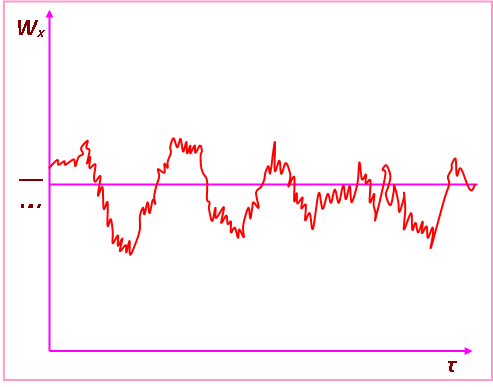
Рис. 2.9. Истинные и усредненная локальные скорости жидкости
при турбулентном движении

Уравнение Бернулли

Решение уравнений движения Эйлера для установившегося потока жидкости приводит к одному из наиболее важных и широко используемых уравнений гидродинамики – уравнению Бернулли.

После умножения левых и правых частей дифференциальных уравнений(2.54) и (2.56)на 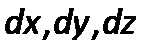и деления их на плотность жидкости 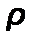получим

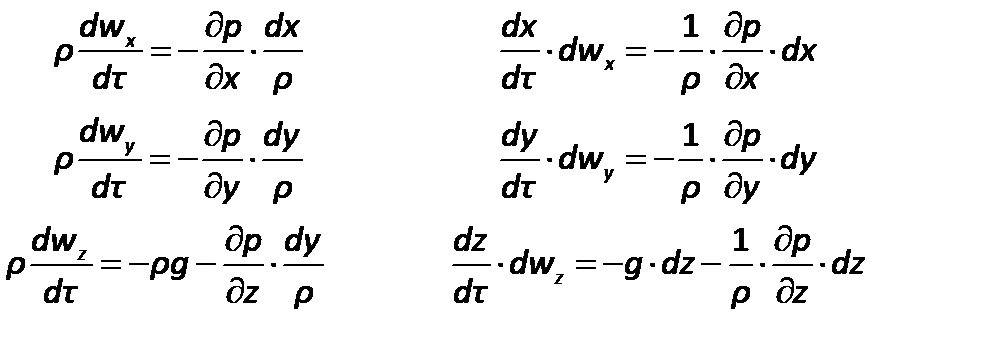(2.54)

Сложим эти уравнения, учитывая, что производные 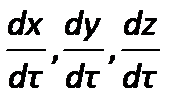выражают проекции 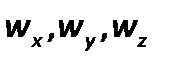скорости на соответствующие оси координат,и получим

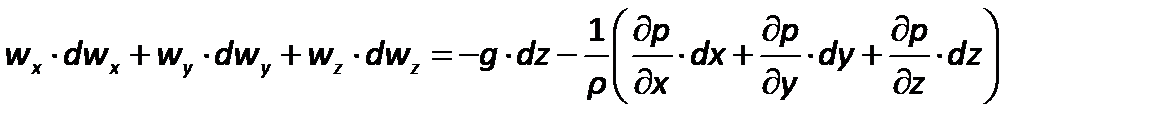(2.55)

Слагаемые левой части уравнения могут быть представлены как

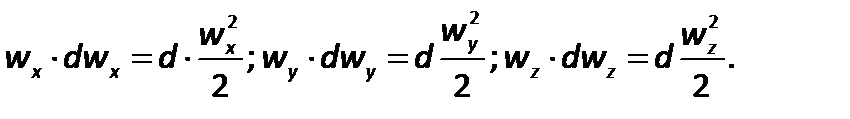(2.56)

а их сумма

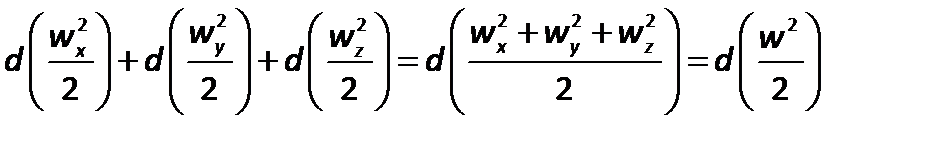(2.57)

В то же время сумма членов, стоящих в скобках в правой части записанного уравнения, представляет собой полный дифференциал давления 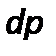(при установившихся условиях давление зависит лишь от положения точки в пространстве и не меняется со временем).

С учетом этих преобразований получим

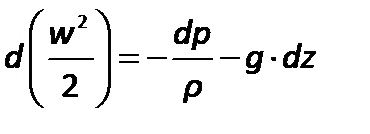(2.58)

Разделив обе части полученного уравнения на ускорение силы тяжести 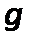и перенеся все члены в левую часть, найдем

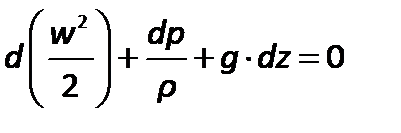(2.59)

Для несжимаемой изотермической жидкости сумма дифференциалов может быть заменена дифференциалом суммы

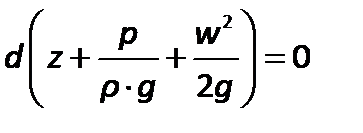(2.60)

тогда после дифференцирования

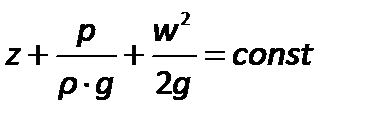(2.61)

Для любых двух поперечных сечений неразрывного потока жидкости уравнение имеет вид (рис. 2.10)

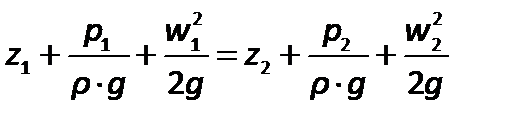(2.62)

Уравнение Бернулли описывает движение идеальной жидкости.

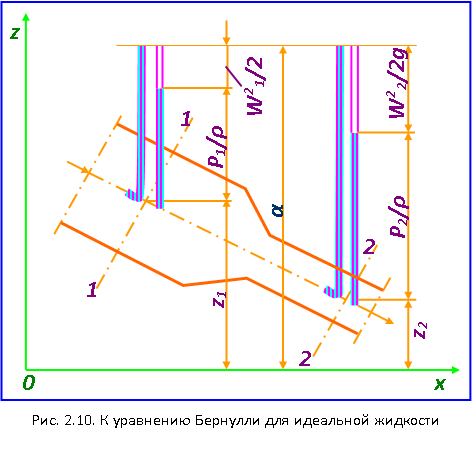
Величина 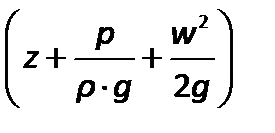представляет собой полный динамический напор.

Согласно уравнению Бернулли, для всех поперечных сечений установившегося потока идеальной жидкости величина гидродинамического напора остается неизменной.

Гидродинамический напор включает три слагаемых, из которых первые два zи 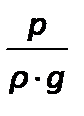входят в основное уравнение гидростатики и представляют собой:

z –нивелирную высоту, называемую также геометрическим напором, представляющую удельную потенциальную энергию положения в данной точке;

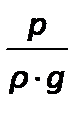– статический или пьезометрический напор характеризует удельную потенциальную энергию давления положения в данной точке;

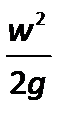– скоростной или динамический напор характеризует удельную кинетическую энергию в данной точке.

Таким образом, уравнение Бернулли имеет определенный энергетический смысл, состоящий в том, что при установившемся движении идеальной жидкости сумма удельной потенциальной 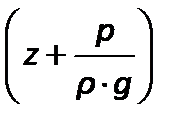и удельной кинетической 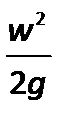энергий жидкости для каждого из поперечных сечений потока остается величиной неизменной.

При изменении поперечного сечения трубопровода и соответственно скорости движения жидкости происходит превращение энергии. При сужении трубопровода часть потенциальной энергии давления переходит в кинетическую, и, наоборот, при расширении трубопровода часть кинетической энергии переходит в потенциальную, но общее количество энергии остается постоянным.

Таким образом, уравнение Бернулли является частным случаем закона сохранения энергии и выражает энергетический баланс потока жидкости.

Для соблюдения баланса энергии при движении реальной жидкости в правую часть уравнения Бернулли должен быть введен член, выражающий потерянный напор. Тогда уравнение Бернулли для реальных жидкостей будет иметь вид

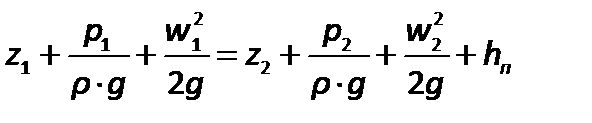(2.63)

Потерянный напор 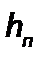характеризует удельную энергию, расходуемую на преодоление гидравлического сопротивления при движении вязкой жидкости.

Если умножить обе части уравнения на 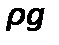, можно получить уравнение Бернулли в ином виде:

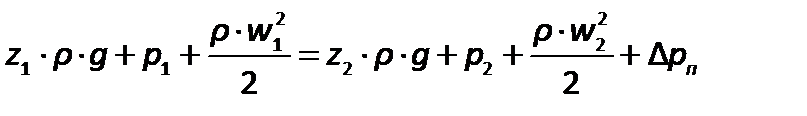(2.64)

.

В уравнении величина 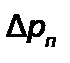– потерянное давление, равное

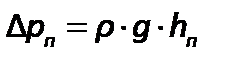(2.65)

Определение потерь напора или давления является практически важной задачей, связанной с расчетом энергии, необходимой для перемещения реальных жидкостей и газов при помощи насосов и компрессоров. Сложность решения этой задачи, как было сказано выше, обусловлена тем, что решение системы дифференциальных уравнений, описывающих движение реальной жидкости, в большинстве случаев оказывается невозможным.

Гидродинамическое подобие

Выше отмечалось, что дифференциальные уравнения Навье–Стокса невозможно решить для большинства технических задач.

Теория подобия позволяет преобразовать уравнения Навье–Стокса и получить из них некоторую общую функциональную зависимость между критериями подобия, характеризующими силы, действующие в потоке при движении вязкой жидкости.

Перепишем уравнение Навье–Стокса для капельной жидкости в развернутом виде для вертикальной оси :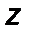

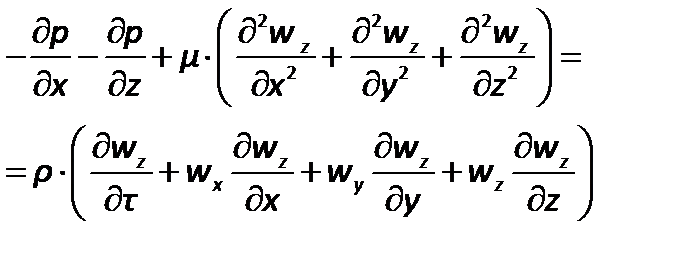(2.69)

Для получения безразмерных комплексов, критериев подобия, необходимо одну часть уравнения разделить на другую. Поскольку каждое из слагаемых уравнения выражает силу, действующую в потоке, то, приняв одну из них за единицу измерения – масштаб сил, безразмерные комплексы будут представлять собой соотношения сил к принятому масштабу. За масштаб сил в движущемся потоке принимается сила инерции.

Если движение жидкости установившееся, то ее скорость не зависит от времени. Член, характеризующий силу инерции после замены дифференциалов конечными величинами (операция отбрасывания знаков математических операторов), будет иметь вид

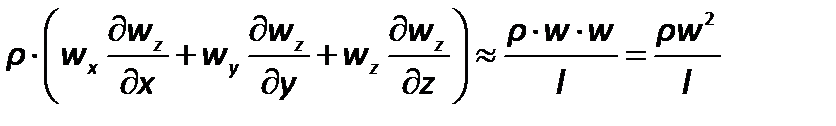(2.70)

где 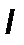– определяющий линейный размер.

Член, отражающий влияние сил тяжести на течение жидкости, рав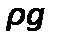ен .Член 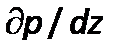, характеризующий влияние сил давления, представляется ввиде

.

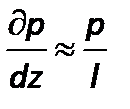Слагаемое, отражающее действие сил трения, представляется как

.

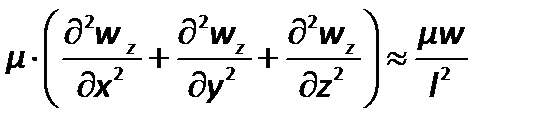Разделим члены одной части уравнения на члены другой его части и установим, таким образом, выражения, характеризующие соотношения между соответствующими силами и силой инерции.

Выражение, характеризующее отношение силы инерции и силы тяжести, называется критерием Фруда:

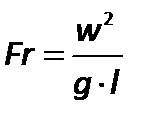(2.71)

Критерий Фруда отражает влияние сил тяжести, или собственного веса, на движение жидкости. Представляет собой меру отношения силы инерции к силе тяжести в подобных потоках.

Соотношение между силами давления и инерции представляет собой критерий Эйлера:

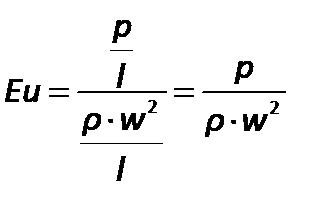(2.72)

Обычно критерию Эйлера придают иной вид, введя в него вместо абсолютного давления разность давлений 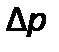между двумя какими-либо точками жидкости:

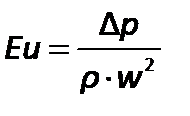(2.73)

Критерий Эйлера отражает влияние перепада гидростатического давления на движение жидкости. Его величина характеризует отношение изменения силы гидростатического давления к силе инерции в подобных потоках.

Безразмерный комплекс, являющийся отношением инерционных сил к силам трения в подобных потоках, представляет известный намкритерий Рейнольдса:

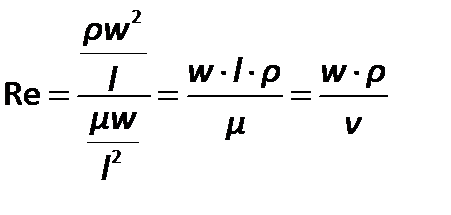(2.74)

Величина 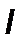в критерии Рейнольдса, как и в других критериях подобия, представляет определяющий линейный размер. При движении жидкости через трубопроводы или аппараты за этот размер принимается диаметр, а в случае некруглого сечения потока – эквивалентный диаметр .

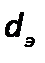При неустановившемся течении жидкости в уравнении Навье–Стокса 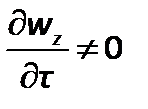. Преобразуем слагаемое, отражающее влияние нестационарности течения, 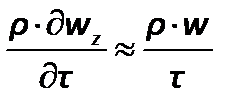. Безразмерный комплекс, полученный отношением силы инерции к члену уравнения, отражающему нестационарный процесс,называется критерием гомохронности:

Классификация основных процессов и аппаратов пищевых производств Вопрос 1: Классификация основных процессов химической технологии. Общая характеристика процессов и аппаратов в химической технологии Тема 1. общие сведения о химической технологии. сырье химической технологии Моделирование и проектирование процессов химической технологии. Иоффе И.Л. Проектирование процессов и аппаратов химической технологии. € Классификация основных процессов и аппаратов Классификация основных процессов химической технологии Оптимизация процессов химической технологии Раздел 1. Теоретические основы процессов химической технологии ← Предыдущая страница | Следующая страница →