Элементарные средства решения систем линейных алгебраических уравнений

При решении инженерных задач достаточно часто приходится сталкиваться с решением систем линейных алгебраических уравнений (СЛАУ). Как известно, обычная СЛАУ может быть представлена в матричном виде как АХ=В, где А — матрица коэффициентов уравнений размера m x n, X — искомый вектор неизвестных с n компонентами и В — вектор свободных членов, также содержащий n компонент. Решением системы называется совокупность чисел 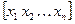, при подстановке которых все уравнения системы обращаются в тождества.

СЛАУ называется совместной, если имеет хотя бы одно решение, и несовместной, если не имеет ни одного решения. Таким образом, решить СЛАУ – значит определить, является ли она совместной или нет.

Существуют точные и приближенные (итерационные) методы решения СЛАУ. К точным относятся методы, которые дают точное решение задачи после конечного числа арифметических и логических операций. К указанным методам относятся, например, матричный метод, метод Крамера, метод Гаусса и т. д. К приближенным – метод Якоби, метод Гаусса – Зейделя и др.

Для определения совместности системы можно использовать теорему Кронекера-Капелли, согласно которой для того, чтобы СЛАУ была совместной, необходимо и достаточно, чтобы ранг матрицы А системы был равен рангу ее расширенной матрицы. Напомним, что расширенная матрица получается после дополнения матрицы коэффициентов столбцом свободных членов. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решение.

На рис. 5.1 представлен пример исследования на совместность следующей системы уравнений:

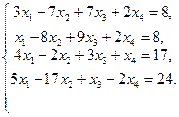
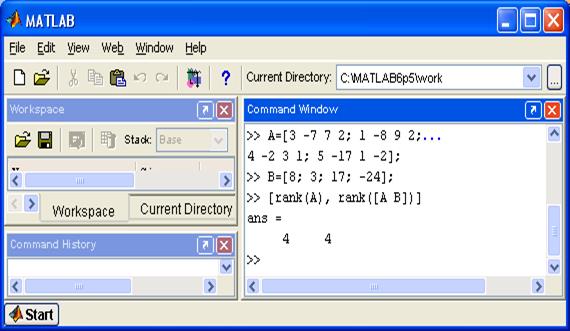
Рис. 5.1. Пример исследования на совместность заданной СЛАУ.

В результате исследования получили, что ранг расширенной матрицы равен рангу матрицы коэффициентов СЛАУ, следовательно, данная система совместна. При этом ранг совместной системы равен числу неизвестных, поэтому система имеет единственное решение.

Рассмотрим точные методы решения СЛАУ в системе MATLAB. Одним из таких методов является матричный метод решения СЛАУ, который предусматривает выполнение следующих шагов:

1. Убедиться в том, что система не является вырожденной (определитель ее не равен нулю), т. е. существует обратная матрица.

2. Найти обратную матрицу .

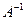3. Найти вектор – столбец X, вычислив произведение .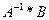

На рис. 5.2 приводится пример решения представленной выше системы уравнений с помощью матричного метода.

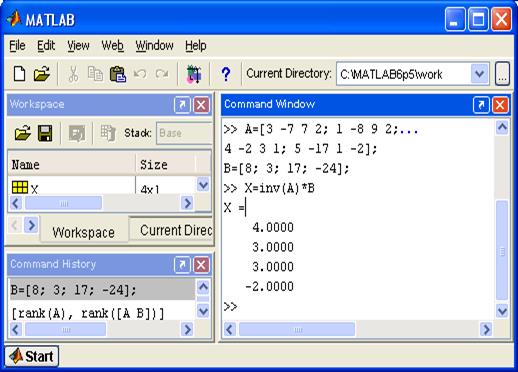
Рис. 5.2. Пример решения СЛАУ с помощью матричного метода.

Рассмотренный матричный метод решения требует определения обратной матрицы, для вычисления которой требуется значительное время, поэтому на практике данный метод не применяется.

В основе решения СЛАУ с помощью формул Крамера лежит теорема Крамера: система n уравнений с n неизвестными, определитель которой отличен от нуля всегда имеет решение, и притом единственное. Значение каждого из неизвестных в этом случае равно дроби, знаменателем которой является определитель системы, а числитель равен определителю системы, в которой вместо столбца коэффициентов при неизвестном располагается столбец свободных членов.

Пусть дана система n линейных уравнений с n неизвестными:

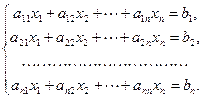
Обозначим 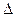определитель системы: 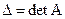. Заменим поочередно столбцы коэффициентов при 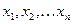на столбец свободных членов и получим n определителей:

.

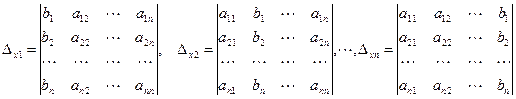Формулы Крамера для решения системы уравнений имеют вид:

.

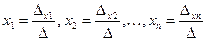Решение СЛАУ из предыдущего примера с помощью формул Крамера представлено на рис. 5.3.

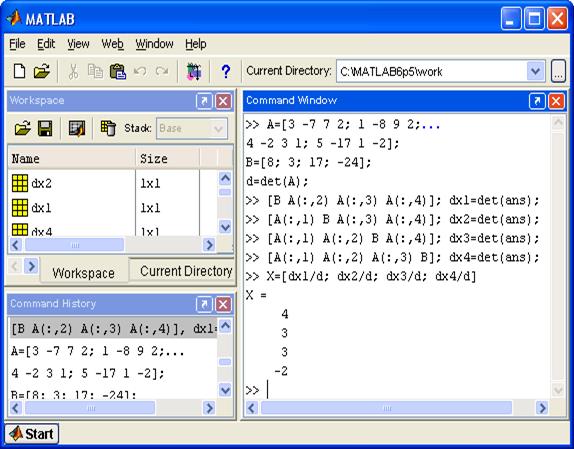
Рис. 5.3. Пример решения СЛАУ с помощью формул Крамера.

Вычисление определителей, используемое в методе Крамера, занимает очень много времени, поэтому этот метод также редко используется на практике.

Существо метода Гаусса состоит в последовательном исключении неизвестных. Систему из n уравнений сначала приводят к равносильной ей системе с треугольной матрицей коэффициентов (прямой ход). Затем выполняют обратный ход, вычисляя значения 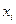и последовательно подставляя их в уравнения для получения значений 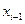. Для уменьшения влияния ошибок округления на решение СЛАУ указанным методом применяют его модификацию – метод Гаусса с частичным выбором главного элемента.

Этот метод в MATLAB реализован в функции rref(), которая на его основании осуществляет приведение расширенной матрицы к треугольной форме. Пример ее применения для решения СЛАУ представлен на рис. 5.4.

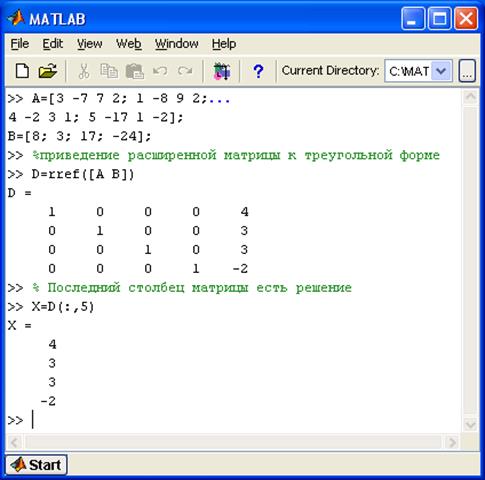
Рис. 5.4. Пример решения СЛАУ с помощью метод Гаусса с частичным выбором главного элемента.

Как было сказано выше, помимо точных методов решения СЛАУ существует ряд итерационных методов. Одним их них является метод наименьших квадратов, реализованный в системе MATLAB функцией lsqr().При вызове функции lsqr(A, B) итерации производятся либо до сходимости к решению, либо до появления ошибки, либо до достижения максимального числа итераций (по умолчанию равного min(20, m, n), где m – число уравнений, n – число неизвестных). Сходимость достигается, когда отношение вторых норм векторов norm(B-Ax)/norm(B) меньше или равно погрешности метода tol (по умолчанию 1е-6). Функция lsqr(A, B, tol) — возвращает решение с заданной погрешностью tol.

На рис. 5.5 приведен пример решения СЛАУ с использованием функции lsqr(A, B). В данном примере процесс итераций сходится на четвертом шаге с относительным остатком (отношением вторых норм векторов невязки и свободных членов) 1.7∙10^-11.

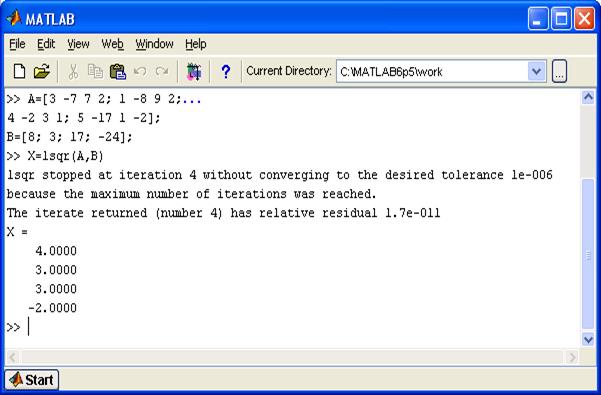
Рис. 5.5. Пример решения СЛАУ методом наименьших квадратов.

Помимо рассмотренных методов решения СЛАУ в MATLAB реализован еще ряд методов решения с помощью функций, расположенных в ядре системы. Описание этих функций можно посмотреть с помощью команды help имя_функции. Функция mldivide() или оператор «\» самостоятельно выбирают лучший метод решения заданной системы уравнений (см. рис. 5.6).

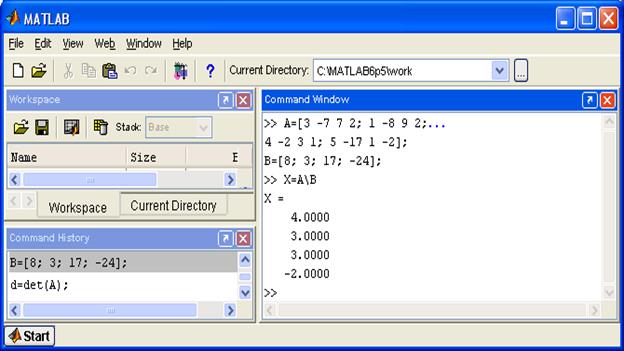
Рис. 5.6. Пример решения СЛАУ.