Основы работы в среде MATLAB
Лабораторная работа № 6
Основы работы в среде MATLAB
ЦЕЛЬ РАБОТЫ:
ü получить навыки работы с основными элементами интерфейса системы MATLAB;
ü получить навыки работы с классами данных в системе MATLAB;
ü изучить основы графической визуализации вычислений в среде MATLAB.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
MATLAB (MATrix LABoratory) —универсальная интегрированная система автоматизации математических расчетов. Особенностью данной системы, выделяющей ее среди прочих пакетов программ аналогичной направленности, является расширенное представление матричных операций, что обусловлено частым применением матриц в сложных математических расчетах, например, при решении задач линейной алгебры и математического моделирования статических и динамических систем и объектов. Слово «интегрированная» указывает на то, что в этой системе объединены удобная оболочка, редактор выражений и текстовых комментариев, вычислитель и графический программный процессор, ориентированный на математические расчеты для реализации численных методов. Благодаря расширенному набору матричных и иных операций и функций, а также наличию множества пакетов расширений система MATLAB применима для расчетов практически в любой области науки и техники.
Важными достоинствами системы являются ее открытость и расширяемость. Большинство команд и функций системы реализованы в виде текстовых m-файлов (с расширением .m) и файлов на языке Си, причем все файлы доступны для модификации. Пользователю дана возможность создавать не только отдельные файлы, но и библиотеки файлов для реализации специфических задач.
ИНТЕРФЕЙС СИСТЕМЫ MATLAB
После загрузки MATLAB появляется Рабочий стол MATLAB, содержащий визуальные инструменты для управления файлами, переменными и приложениями, связанными с системой MATLAB (рис. 4.1). Рабочий стол состоит из строки заголовка, строки главного меню, панели инструментов, области для размещения окон инструментальных средств и строки состояния с кнопкой Start. На Рабочем столе может быть представлено любое сочетание из представленных ниже инструментальных средств:
· окно запуска приложений (Launch Pad);
· окно команд (Command Window);
· окно истории команд (Command History);
· окно просмотра помощи (Help Browser);
· окно просмотра текущей директории (Current Directory Browser);
· окно просмотра Рабочей области (Workspace Browser);
· окно Редактора данных (Array Editor);
· Редактор m– файлов (Editor/ Debugger);
· Профайлер (Profiler), оценивающий быстродействие команд.
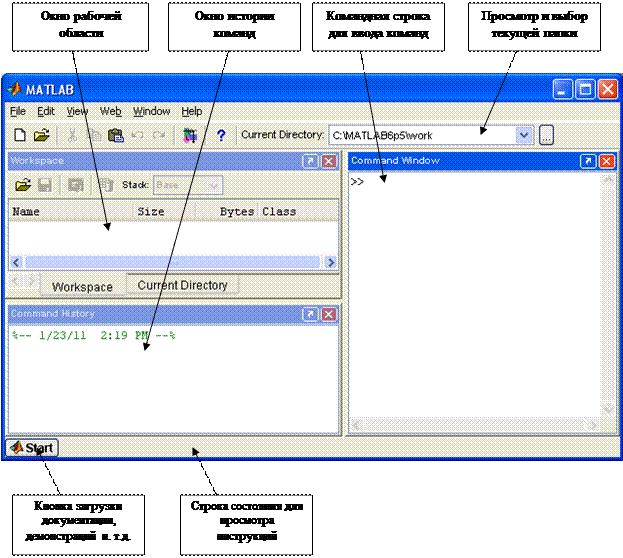Рис. 4.1. Рабочий стол системы MATLAB.
Помимо указанных инструментальных средств в систему MATLAB входят не управляемые посредством Рабочего стола графические окна (Figures), предназначенные для визуализации результатов вычислений.
Для управления окнами инструментальных средств предназначены команды меню View. Например, команда Desktop Layout открывает меню, в котором размещаются команды, предназначенные для отображения на Рабочем столе системы различных комбинаций инструментальных средств. Наиболее используемым расположением окон инструментальных средств при работе с системой MATLAB является расположение, принятое по умолчанию. Это расположение при необходимости можно установить командой View→ Desktop Layout→Default.
Для осуществления операций на файловом уровне предназначены команды меню File. Так с помощью подменю New можно открыть приложение для создания нового m – файла (Editor/ Debugger), динамической модели(SIMULINK), графического интерфейса пользователя (GUIDE), а также создать новое графическое окно. Команда Save Workspace as… позволяет сохранять данные, расположенные в рабочей области, на диске в виде двоичных файлов с расширением .mat. Для этих же целей служит и команда save. Например, вызов команды save fname X позволит записать значение переменной X в файл fname.mat. Следует отметить, что возможности сохранения всего текста сессии, формируемой в командном режиме, команда save не дает, для этого служит команда diary. Например, вызов команды diary filename приведет к записи на диск всех команд в строках ввода и полученных результатов в виде текстового файла с именем filename.m. Кроме того, в системе предусмотрена возможность приостановки записи в файл с помощью команды diary off и возобновления ранее прерванной записи с помощью команды diary on.
Для загрузки рабочей области ранее сохраненной сессии предназначена команда load. Например, для загрузки ранее сохраненного файла myf_1.mat следует вызвать команду load myf_1.mat. Если команда load используется в ходе проведения сессии, то произойдет замена текущих значений переменных теми значениями, которые были сохранены ранее в считываемом МАТ-файле. При этом для задания имен загружаемых файлов может использоваться знак *, означающий загрузку всех файлов с определенными признаками. Например, load lab*.mat означает загрузку всех файлов с началом имени lab, например lab_1, lab_2, lab_3 и т. д.
Для завершения работы с системой можно использовать команды exit, quit или комбинацию клавиш Ctrl+Q. Если необходимо сохранить значения всех переменных системы, то перед вводом команды exit следует дать команду save. В этом случае команда load после загрузки системы считает значения сохраненных переменных и позволит начать работу с системой с того момента, когда она была прервана.
Команды меню Edit позволяют отменять(Undo) или возвращать (Redo) отмененное действие, обмениваться информацией с буфером обмена (Cut–Вырезать, Copy– Копировать, Paste – Вставить, PasteSpecial – Специальная вставка), полностью выделять содержимое текущего окна (Selectall), а также очищать окно команд (ClearCommandWindow), окно истории команд (ClearCommandHistory) и содержимое рабочей области ( ClearWorkspace).
Команды меню Web позволяют перейти на страницу сайта фирмы разработчика системы MATLAB. Для переключения между окнами m– файлов, окнами библиотек блоков приложения SIMULINK, окнами моделей систем предназначены команды меню Windows. Доступ к справочной информации предоставляют команды меню Help.
Командное окно (Command Window) предназначено для ввода команд и вывода результатов их выполнения в текстовом режиме. Работа с командным окном происходит в диалоговом режиме. Пользователь вводит команду в командную строку после приглашения >> и нажимает Enter, после чего команда передается ядру системы MATLAB. Ядро проверяет команду на синтаксические ошибки и, в случае их отсутствия, выполняет команду и возвращает результат. В противном случае выводится сообщение об ошибке.
По умолчанию в командное окно результат выводится в числовом формате shortG. Изменить формат вывода числа можно с помощью диалогового окна Preferences, которое вызывается одноименной командой меню File. В данном окне после активизации инструментального средства Command Window из раскрывающегося списка поля Numeric format, расположенного внутри группы Text display, следует выбрать необходимый формат. Помимо этого сменить текущий формат можно также с помощью команды format. Список форматов вывода числовых данных представлен в таблице 4.1.
Таблица 4.1. Форматы вывода числовых данных.
| Формат | Описание | Пример |
| short | Короткое число с фиксированной точкой (под дробную часть отводится четыре разряда) | 1.3333 |
| long | Длинное число с фиксированной точкой (под дробную часть отводится четырнадцать разрядов) | 1.33333333333333 |
| shortE | Короткое число с плавающей точкой (под дробную часть отводится четыре разряда) | 1.3333e+000 |
| longE | Длинное число с плавающей точкой (под дробную часть отводится пятнадцать разрядов) | 1.333333333333338e+007 |
| shortG | Выбирается наилучшая форма представления числа из форматов short и short e | |
| longG | Выбирается наилучшая форма представления числа из форматов long и long e | |
| hex | Число выводится в шестнадцатеричной форме | 4010СВ |
| bank | Формат представления долларов и центов | 69.96 |
| + | Символьное обозначение числа: «+» – положительное число; «-» – отрицательное число; пробел – нулевое значение. | |
| rational | Число выводится в дробном виде | 1/3 |
Заметим, что задание формата сказывается только на форме вывода чисел и не влечет за собой изменения самого числа.
Переменные и определения новых функций в системе MATLAB хранятся в особой области памяти, именуемой рабочей областью (workspace). Для быстрого просмотра атрибутов объектов, располагающихся в рабочей области, их редактирования, сохранения и удаления предназначено Окно просмотра рабочей области (Workspace Browser) (рис. 2 ). В этом окне можно увидеть имя переменной, ее размер, число байтов, занимаемых переменной в памяти, и ее класс.
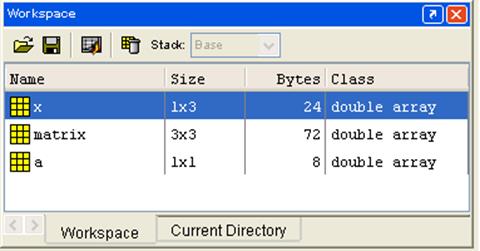
Рис. 4.2. Окно просмотра рабочей области.
Для просмотра и редактирования значений выделенной переменной предназначена кнопка Open (Открыть) 
палитры инструментов Workspace Browser, которая вызывает окно редактирования Array Editor. Указанное окно дает возможность быстрого доступа к любому элементу массива, позволяет менять тип значений элементов (меню Numeric format ), позволяет изменять число строк и столбцов массива (рис. 3). Палитра инструментов Workspace Browser позволяет также загружать данные из файла в рабочую область ( 
), удалять выделенный объект ( 
), сохранять рабочую область в файле ( 
). Дополнительные функции по работе с Workspace Browser можно получить из контекстно–зависимого меню, вызываемого щелчком правой кнопки мыши по объекту в окне просмотра рабочей области.
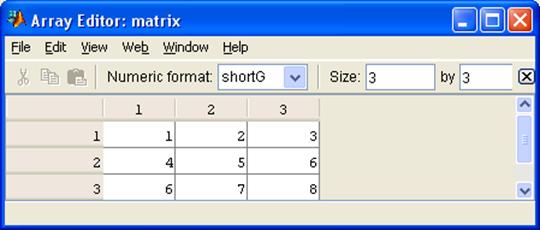
Рис. 4.3.Окно редактора данных.
Просматривать содержимое рабочей области, загружать и удалять данные можно также с помощью Command Window. Для просмотра имен переменных, находящихся в рабочей области, предназначена команда who. Полную информацию о содержании рабочей области дает команда whos, которая выводит в командное окно общее количество переменных и общий объем занимаемой ими памяти. Для очистки рабочей области используется функция clear . Например, clear x — уничтожит определение переменной х. Команда clear без параметров стирает все переменные.
Окно истории команд (Command History) служит для просмотра команд, заданных ранее в командной строке, даты и времени начала сеанса работы с системой. С помощью контекстного меню окна истории команд можно выполнять следующие действия: копировать (Copy) выделенные строки в буфер обмена, повторно выполнять команду или серию выделенных команд (Evaluate Selection), создавать новый m-файл (Create M-file) путем копирования выделенных строк в редактор m-файлов Editor/ Debugger, а также удалять выделенные строки(Delete Selection), удалять все строки из окна истории команд до выделенной строки (Delete to Selection) и полностью очищать окно истории команд (Delete Entire History).
Окно просмотра текущей директории (Current Directory Browser) дает возможность создания, переименования, удаления файлов и директорий, возможность перемещения по структуре директорий, просмотра содержания текущей директории и атрибутов файлов (тип, дата последнего изменения, краткое описание файла).
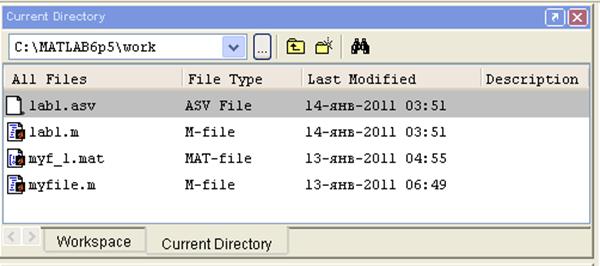
Рис. 4.4. Окно просмотра текущей директории.
КЛАССЫ ДАННЫХ
Данные в MATLAB группируются по классам. Все классы данных являются матричными и поддерживают работу с разреженными матрицами, где преобладают нулевые элементы.
Арифметические классы данных делятся на целые и вещественные. При этом данные целого класса могут быть числами со знаком и без знака, а вещественного – числами одинарной (single – 4 байта) и двойной (double – 8 байт) точности. При создании переменной она по умолчанию получает класс double, так как все числа при выполнении арифметических операций в системе MATLAB должны быть числами двойной точности. Остальные арифметические классы предназначены для эффективного хранения данных на диске.
В таблице 4.2 приводится список арифметических операторов и соответствующих им функций и синтаксис их применения. Заметим, что все операции в MATLAB реализуются посредством вызова соответствующих функций.
Таблица 4.2. Арифметические операторы и функции MATLAB.
| Название функции | Оператор | Знак оператора | Синтаксис |
| plus | Плюс | + | М1 + М2 |
| uplus | Унарный плюс | + | +М |
| minus | Минус | – | М1 – М2 |
| uminus | Унарный минус | – | –М |
| mtimes | Матричное умножение | * | М1 * М2 |
| times | Поэлементное умножение массивов | .* | А1 .* А2 |
| mpower | Возведение матрицы в степень | ^ | М1^х |
| power | Поэлементное возведение массива в степень | .^ | A1 .^ x |
| mldivide | Обратное (справа налево) деление матриц | \ | M1\M2 |
| mrdivide | Деление матриц слева направо | / | М1/М2 |
| ldivide | Поэлементное деление массивов справа налево | .\ | А1 .\ А2 |
| rdivide | Поэлементное деление массивов слева направо | . / | А1 ./ А2 |
В отличие от большинства языков программирования в системе MATLAB практически все операторы предназначены для выполнения операций над массивами, поэтому существует две различные операции, связанные с умножением, делением и возведением в степень. Например, оператор *означает умножение матриц, а оператор .* —поэлементное умножение матриц. Примеры использования некоторых из приведенных в таблице арифметических операторов приводятся на рис 4.5.
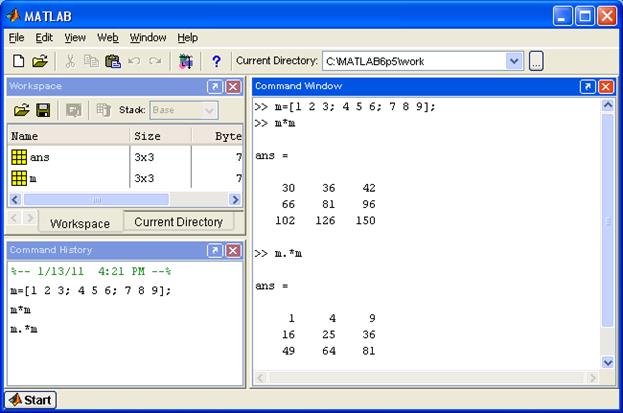
Рис. 4.5. Примеры использования операторов * и .*.
Тригонометрические и обратные тригонометрические функции, определенные в системе MATLAB, вычисляются для каждого элемента массива. При этом, все углы в функциях задаются в радианах. Приведем некоторые из указанных функций:
acos (X) — возвращает арккосинус для каждого элемента X;
acot (X) — возвращает арккотангенс для каждого элемента X;
asin(X) — возвращает арксинус для каждого элемента X;
atan(X) — возвращает арктангенс для каждого элемента X.
cos(X) — возвращает косинус для каждого элемента X;
cot(X) — возвращает котангенс для каждого элемента X;
sin(X) — возвращает синус для каждого элемента X;
tan(X) — возвращает тангенс для каждого элемента X;
cosh(X) — возвращает гиперболический косинус для каждого элемента X.
К основным математическим функциям системы MATLAB относятся также следующие функции:
abs(X) — возвращает абсолютную величину для каждого числового элемента вектора X;
ехр(Х) — возвращает экспоненту для каждого элемента X;
factor(n) — возвращает вектор-строку, содержащую простые множители числа n (для массивов эта функция неприменима);
G=gcd(A, В) — возвращает массив, содержащий наибольшие общие делители соответствующих элементов массивов целых чисел А и В;
lcm(A,B) — возвращает наименьшие общие кратные для соответствующих парных элементов массивов А и В (любой из аргументов А или В может быть скаляром);
log (X) — возвращает натуральный логарифм элементов массива X.
log2(X) — возвращает логарифм по основанию 2 элементов массива X;
log10(X) — возвращает логарифм по основанию 10 для каждого элемента X.
mod(X, Y) — возвращает остаток от деления X на Y;
pow2(Y) — возводит в квадрат каждый элемент массива Y;
primes(n) — возвращает вектор-строку простых чисел, меньших или равных n;
sqrt(A) — возвращает квадратный корень каждого элемента массива А.
Наряду с числовыми данными система MATLAB позволяет работать с данными, которые являются последовательностью символов. Переменные, содержащие только символы, относятся к символьному классу. Значения переменных данного класса заключаются в апострофы, например, text=’Unix’. Каждый символ в подобной переменной занимает в памяти 2 байта.
Система MATLAB позволяет также создавать двухмерные массивы символов – массивы строк. При этом количество символов в каждой из строк должно быть одинаковым, в противном случае в командное окно будет выдаваться сообщенное об ошибке. Для выравнивания числа символов в строках обычно используются пробелы, добавляемые в конец строки.
Данные логического класса могут принимать одно из двух значений: true (истина), которая ассоциируется с единицей, или false (ложь), ассоциирующуюся с нулем. Переменная логического класса занимает в памяти 1 байт. Значения логического класса получаются как результат операций отношения, список которых приводится в таблице 4.3.
Таблица 4.3. Операторы и функции отношения
| Название функции | Оператор | Знак оператора | Синтаксис |
| eq | Равно | = = | x = = y |
| ne | He равно | ~ = | x ~ = y |
| lt | Меньше чем | < | x<y |
| gt | Больше чем | > | x>y |
| le | Меньше или равно | <= | x<=y |
| ge | Больше или равно | >= | x>=y |
В общем случае операторы отношения поэлементно сравнивают два массива одного размера и выдают результат в виде массива того же размера, как показано на рис. 4.6.
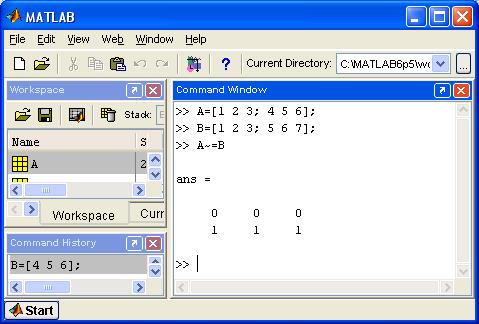
Рис. 4.6. Пример использования оператора He равно.
Если один из операндов — скаляр, происходит сравнение всех элементов второго операнда-массива со значением этого скаляра (рис. 4.7).
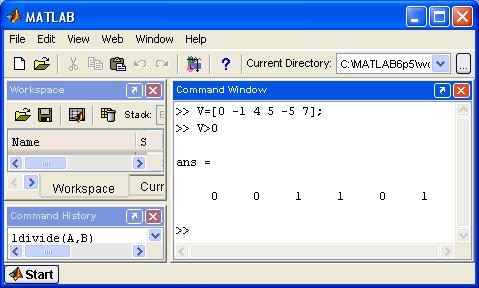
Рис. 4.7. Пример сравнения элементов массива со скаляром.
Также возможно применение операторов отношения и к символьным выражениям. В этом случае символы, входящие в выражения, представляются своими ASCII-кодами, а строки воспринимаются как векторы, содержащие значения кодов (рис. 4.8).
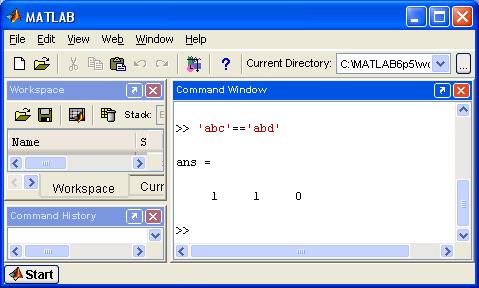
Рис. 4.8. Пример сравнения символьных выражений.
Логические операторы и соответствующие им функции служат для реализации поэлементных логических операций над элементами одинаковых по размеру массивов (табл. 4). При этом аргументами логических операторов могут быть и числа, и строки. При аргументах числах – логический нуль соответствует числовому нулю, а любое отличное от нуля число воспринимается как логическая единица. Для строк действует уже отмеченное правило — каждый символ строки представляется своим ASCII-кодом.
Таблица 4.4. Логические операторы и функции MATLAB
| Название функции | Оператор | Знак оператора | Синтаксис |
| and | Логическое И | (AND) & | and(A,B) А&В |
| or | Логическое ИЛИ | (OR) | | оr(А,В) А|В |
| not | Логическое НЕ | (NOT) ~ | not(А) ~B |
| хог | Исключающее ИЛИ | XOR | xor(A,B) |
| any | Верно, если все элементы вектора равны нулю | any | any(A) |
| all | Верно, если все элементы вектора не равны нулю | all(B) |
К классу операторов в системе MATLAB относятся также специальные символы. Они предназначены для создания самых разнообразных объектов входного языка и языка программирования системы и придания им различных форм. Рассмотрим некоторые из них.
Для формирования упорядоченных числовых последовательностей в MATLAB используется оператор : (двоеточие), имеющий следующий вид
Начальное_значение : Шаг : Конечное_значение
Данный оператор порождает последовательность чисел, которая начинается с Начального значения, идет с заданным Шагом и завершается Конечным значением, Если Шаг не задан, то он принимает значение 1. Подобные последовательности могут, например, потребоваться для создания значений абсциссы при построении графиков. Пример использования данного оператора приводится на рис. 4.9.
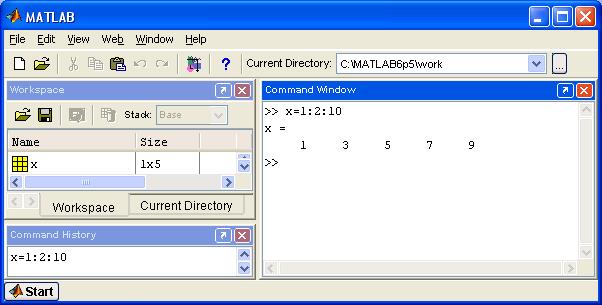
Рис. 4.9. Пример использования оператора : (двоеточие).
Система MATLAB специально предназначена для проведения сложных вычислений с векторами, матрицами и массивами, поэтому по умолчанию она предполагает, что каждая заданная переменная — это вектор, матрица или массив. Например, если задано А = 10, то это значит, что А — это матрица размера 1 х 1. Для формирования векторов и матриц используются символы [ ] (квадратные скобки). Так при задании вектора значения его элементов следует перечислить в квадратных скобках, разделяя пробелами, например, V = [l 2 3]. В результате будет создан вектор – строка размера 1 х 3. Для создания вектор – столбца вводимые элементы нужно разделять точкой с запятой «;». Например, присваивание V = [l; 2; 3] задает вектор – столбец размером 3 х 1.
Задание матрицы требует указания нескольких строк, для разграничения которых используется знак ; (точка с запятой). Этот же знак в конце ввода предотвращает вывод матрицы или вектора (и вообще результата любой операции) на экран дисплея. Так, присваивание М = [1 2 3; 4 5 6; 7 8 9] задает квадратную матрицу, содержащую три строки и три столбца. Элементы матриц и векторов можно также вводить в виде арифметических выражений, содержащих любые доступные системе функции, например, V = [17+55/(4+7) exp(14) sqrt(225)].
Для доступа к отдельному элементу вектора или матрицы следует указать имя требуемого вектора / матрицы и индекс (индексы) элемента в круглых скобках. Так, например, если обратиться к элементу М(2, 2), приведенной выше матрицы М, то результат будет равен 5.
Оператор : (двоеточие) позволяет также выбирать строки, столбцы и элементы из векторов, матриц и многомерных массивов:
А(: , j) — j-й столбец матрицы А;
А(i,:) — i-я строка матрицы А;
A(j:k) — A(j), A(j+l),...,A(k);
А(:) — записывает все элементы массива А в виде столбца.
Например, если требуется всем элементам третьего столбца матрицы М присвоить значение 7, то можно воспользоваться следующим выражением М(: , 3) = 7. В следующем примере элементы второй строки матрицы М умножаются на -2: M(2,:)* -2.
Для удаления отдельных столбцов или строк матриц используются пустые квадратные скобки [ ]. Например, для удаления второй строки матицы М можно использовать выражение М(2, :) = [].
Знак процента % используется для указания логического конца строки. Текст, находящийся после знака процента, воспринимается как комментарий и игнорируется (за исключением русскоязычных комментариев, которые нередко ведут к ошибочным командам).
В выражениях могут использоваться любые операции, а также их комбинации. При этом последовательность выполнения операций соответствует их приоритету. Рассмотрим приоритеты операций, начиная с наивысшего.
1. Операции транспонирования, поэлементного возведения в степень, матричного возведения в степень.
2. Унарные операции (т. е. применяемые к одному оператору): +, –, ~ (логическое отрицание).
3. Мультипликативные операции: умножение, деление.
4. Аддитивные операции: сложение, вычитание.
5. Оператор двоеточие «:».
6. Операторы отношения.
7. Логическое И.
8. Логическое ИЛИ.
Рис. 4.10. Построение графика синусоиды.
В одном графическом окне можно одновременно построить графики сразу нескольких функций. Например, можно задать переменные y1=sin(x); y2=cos(x); , а затем вызвать команду plot(x,y1,x,y2). Результат построения можно увидеть на рис. 4.11.
Рис. 4.11. Пример построения в одном графическом окне графиков двух функций.
Команда plot(X,Y,S) — аналогична команде plot(X,Y), но с помощью третьего параметра, строковой константы S, она дает возможность задавать тип линии графика. Значения константы S приведены в таблице 4.5.
Таблица 4.5. Значения параметра S команды plot(X,Y,S).
| Цвет линии | Тип маркера | ||
| Y | Желтый | . | Точка |
| М | Фиолетовый | Окружность | |
| С | Голубой | X | Крест |
| R | Красный | + | Плюс |
| G | Зеленый | * | Звездочка |
| В | Синий | S | Квадрат |
| W | Белый | D | Ромб |
| К | Черный | V | Треугольник (вниз) |
| А | Треугольник (вверх) | ||
| < | Треугольник (влево) | ||
| > | Треугольник (вправо) | ||
| Р | Пятиугольник | ||
| Тип линии | |||
| – | Сплошная | ||
| ; | Двойной пунктир | ||
| –. | Штрих-пунктир | ||
| – – | Штриховая |
Рассмотрим пример построения графиков трех функций с различным стилем представления каждой из них. Сначала зададим интервал изменения аргумента и сами функции y1, y2, и y3, а затем применим команду plot(x, yl,'- m',x, y2,'-. + r',x,y3,'- - o k'), как это представлено на рис. 4.12.
Рис. 4.12. Пример применения команды plot(X,Y,S).
Результат построения продемонстрирован на рис. 4.13.
Рис. 4.13. Пример построения графиков трех функций с различным стилем представления каждой из них.
Для построения графиков функций со значениями х и у, изменяющимися в широких пределах, как правило, используются логарифмические масштабы для координатных осей X и У. Для построения графика в этом случае используется команда loglogx(), синтаксис которой аналогичен ранее рассмотренному для функции plot(). Логарифмический масштаб используется. Ниже дан пример применения данной команды:
>>x=logspace(-1,3);
>>loglog(x, exp(x)./x)
>>grid on
Обратите внимание на то, что командой grid on строится координатная сетка. На рис. 4.14 представлен график функции ехр(х)/х в логарифмическом масштабе, о чем свидетельствует неравномерное расположение линий координатной сетки.
Рис. 4.14. График функции ехр(x)/x в логарифмическом масштабе.
В некоторых случаях предпочтителен полулогарифмический масштаб графиков, когда по одной оси задается логарифмический масштаб, а по другой — линейный. Для построения графиков функций в подобных случаях используются следующие команды:
· semilogx() — строит график функции в логарифмическом масштабе (основание 10) по оси X и линейном по оси Y;
· semilоgу () — строит график функции в логарифмическом масштабе по оси Y и линейном по оси X.
Запись параметров для представленных функций выполняется по аналогии с функцией plot().
Построение графика линии на плоскости в полярной системе координат осуществляется с помощью функции polar (phi, rho, s), где phi – задает полярный угол в радианах, rho – полярный радиус, а необязательный аргумент s служит для задания свойств линии и маркеров. Например, последовательный вызов приведенных ниже команд сформирует графическое окно представленное на рис. 4.15.
>> t=0:pi/50:2*pi;
>> polar(t,sin(5*t))
Рис. 4.15. Пример построения графика в полярной системе координат.
В прикладных расчетах часто встречаются графики, именуемые столбцовыми диаграммами, отражающие содержание некоторого вектора V. Особенно часто этот тип диаграмм используются при представлении данных финансово-экономических расчетов. При этом каждый элемент вектора представляется столбцом, высота которого пропорциональна значению элемента. Столбцы нумеруются и масштабируются по отношению к максимальному значению наиболее высокого столбца. Выполняет построение такого графика одна из следующих команд:
bar(x, Y) — строит столбцовый график элементов вектора Y (или группы столбцов для матрицы Y) со спецификацией положения столбцов, заданной значениями элементов вектора х, которые должны идти в монотонно возрастающем порядке;
bar(Y) — строит график значений элементов матрицы Y, а в качестве х используется вектор х=1:m;
BAR(Y,WIDTH) — команда аналогична ранее рассмотренным, но со спецификацией ширины столбцов (при WIDTH > 1 столбцы в одной и той же позиции перекрываются). По умолчанию задано WIDTH = 0.8.
По аналогии с командой plot в приведенных командах построения столбцовых диаграмм возможно задание спецификаций графиков, например типа линий, цвета и т. д. Спецификация 'stacked' задает рисование всех n столбцов в позиции m друг на друге, как это представлено на рис. 4.16. Помимо команды bar() существует аналогичная ей по синтаксису команда barh(), которая" строит столбцовые диаграммы с горизонтальным расположением столбцов.
Рис. 4.16. Пример построения диаграммы с вертикальными столбцами
Закрашенные секторы часто используются для построения цветных плоских круговых диаграмм. Для их построения в MATLAB служит команда piе:
pie(X) — строит круговую диаграмму по данным нормализованного вектора X/ SUM(X). При этом, если SUM(X)<=1.0, то значения в X непосредственно определяют площадь секторов;
pie(X,EXPLODE) — строит круговую диаграмму, у которой отрыв секторов от центра задается вектором EXPLODE, который должен иметь тот же размер, что и вектор данных X.
Система MATLAB также предоставляет возможность построения объемных круговых диаграмм с помощью команды pie3(), аналогичной команде pie(). На рис. 4.17 демонстрируется пример построения двух видов круговых диаграмм: плоской и объемной. В качестве исходных данных в обоих случаях берется вектор Х=[1 2 3 4 5]. Для построения плоской диаграммы используется команда pie(X,[1 1 1 1 1]), а для объемной – pie3(X,[1 1 1 1 1]).
Рис. 4.17. Пример построения круговых диаграмм.
В системе MATLAB предусмотрена также возможность построения графиков в полярной системе координат. Напомним, что в данной системе координат любая точка представляется как конец радиус-вектора, исходящего из начала системы координат под углом ТНЕТА к горизонтали и имеющего длину R. Для построения графика в этом случае используется команда polar(THETA ,R, S), где параметр THETA обычно меняется от 0 до 2*pi, а строковая константа S, задающая стиль построения, не является обязательным параметром.
Команда plot3(X,Y,Z,S) является аналогом команды plot (), но относится к функции двух переменных z(x, у). Она строит аксонометрическое изображение трехмерных поверхностей, определяемых матрицами одинакового размера X, Y и Z. Совместно с функциями построения графиков трехмерных поверхностей обычно используется функция meshgrid, формирующая двумерные массивы X и Y. Например, для преобразования области, заданной векторами х и у, в массивы X и Y, которые могут быть использованы для вычисления функции двух переменных и построения трехмерных графиков, можно воспользоваться выражением [X, Y] = meshgrid(x, y). При этом, строки выходного массива X будут являться копиями вектора х; а столбцы Y — копиями вектора у (рис. 4.18).
Рис. 4.18. Пример использования функции meshgrid().
Рассмотрим пример построения трехмерной поверхности, описываемой функцией 
. Листинг необходимый для построения команд приведен на рис. 4.19.
Рис. 4.19. Построение поверхности, описываемой функцией .
Результат построения демонстрируется на рис. 4.20.
Рис. 4.20. График поверхности, построенный линиями.
Наиболее представительными и наглядными являются сетчатые графики поверхностей с заданной или функциональной окраской. Для их построения предназначена функция mesh(X,Y,Z,C), которая выводит в графическое окно сетчатую поверхность Z(X.Y) с цветами узлов поверхности, заданными массивом С. При этом параметр C не является обязательным, то есть допустим вызов команды mesh(X,Y,Z). В этом случае C=Z и используется функциональная окраска, при которой цвет задается высотой поверхности. Пример построения сетчатого графика поверхности, описываемой функцией , с использованием функциональной окраски представлен на рис. 4.21.
Рис. 4. 21. Сетчатый график поверхности с функциональной окраской.
При использовании функциональной окраски весьма полезным является вывод шкалы цветов командой colorbar. Ее варианты перечислены ниже:
colorbar( 'vert') — выводит вертикальную шкалу цветов на текущий график (см. рис. 4.21);
colorbar( 'horiz') — выводит горизонтальную шкалу цветов на текущий график;
colorbar — устанавливает в текущий график новую вертикальную шкалу цветов или обновляет уже имеющуюся.
Иногда график поверхности полезно объединить с контурным графиком ее проекции на плоскость, расположенным под поверхностью. Для этого используется команда meshc(), аналогичная команде mesh(), но помимо графика поверхности строящая изображение ее проекции в виде линий равного уровня, что дает наилучшее представление об особенностях поверхности.
После того как график уже построен, MATLAB позволяет выполнить его форматирование в нужном виде. Для форматирования графиков в системе предназначены команды Figure Properties (Свойства рисунка), Axis Properties (Свойства осей) и Current ObjectProperties (Свойства текущего объекта)менюEdit графического окна. С помощью перечисленных команд можно,