Контактная нелинейность, вызванная, в частности, переменными размерами фактической зоны контакта.
Основные причины геометрической нелинейности:
– потеря устойчивости упругой системы при некоторой предельной деформации;
– изменение направления действия нагрузки вследствие деформации упругой системы.
Если стержень сжимать силами, действующими точно вдоль оси, то при нагрузке F, меньшей некоторой FКР, он будет укорачиваться, сохраняя свою форму. При нагрузке F>FКР прямолинейная форма равновесия становится энергетически невыгодной (неустойчивость по Эйлеру) и стержень начнет выпучиваться, искривляться. Похожие проблемы могут возникнуть для тела любой формы.
Для анализа устойчивости упругой системы в конечно-элементных пакетах обычно используются расчет типа Buckling («потеря устойчивости»). Для этого исследуемую конструкцию нагружают фактически действующей силой. Результатом расчета является число, показывающее, во сколько раз критическая сила FКР превышает приложенную нагрузку. Также рассчитывается формы, которые может приобрести исследуемая система после потери устойчивости.
Примером проявления геометрической нелинейности, вызванной изменением направления действия нагрузки при деформации, может служить изгиб стержня, нагруженного и вдоль и поперек оси (рисунок 4.2.14). При изгибе стержня под действием поперечной силы R линия действия продольной силы P отклоняется от оси стержня на величину D. В результате возникает дополнительный момент M=P´D, способствующий дальнейшему увеличении поперечной деформации. В свою очередь, увеличение поперечной деформации вызывает увеличение изгибающего момента от силы Р и т.д. В результате воздействие небольшой силы R может приводить к весьма значительному изгибу стержня.
Нелинейный расчет необходимо проводить, если по результатам линейного расчета деформация конструкции одного порядка с ее размерами. Например, достаточно часто деформация оболочки может значительно превышать ее толщину. В этом случае к результатам оценки напряжений по результатам статического расчета следует относиться с определенной настороженностью, и желательно выполнять еще и нелинейный расчет, а также расчет на устойчивость.
Физическая нелинейность возникает при использовании в расчетах материалов с нелинейной зависимостью деформации от приложенных нагрузок (напряжений) и/или зависимостью деформации от времени. Например, такая нелинейность возникает при использовании упруго-пластичных(elasto-plastic) илинелинейно-упругих (non-linear elastic) материалов.Примером зависимости деформации от времени может служить такое явление, как ползучесть (creep). При ползучести кратковременное воздействие нагрузки не вызывает пластической деформации, но при длительном воздействии той же самой нагрузки, особенно при повышенной температуре, деталь начинает «течь» (пластически деформироваться).
Главными причинами контактной нелинейности является а) трение в зоне контакта тел; б) нелинейная связь между фактической площадью контакта и величиной нагрузки.

Рисунок 4.2.14 – Причина возникновения геометрической нелинейности
15. Виды конечно-элементных расчетов. Динамическиерасчеты
Динамические расчеты обеспечивают решение следующих типовых задач:
– анализ нестационарных переходных процессов в объекте при сравнительно кратковременном (импульсном) действии нагрузки (Transient Dynamic/Time History);
– исследование динамической реакции объекта на достаточно длительное периодическое воздействие внешних факторов (Frequency/Harmonic Response);
– определение собственных частот и форм колебаний (Normal Modes/Eigenvalues).
Под нестационарным переходным процессом обычно понимают поведение конструкции в начальный период времени, когда ее движение еще не установилось и складывается из собственных колебаний и вынужденного движения, вызванных приложенной нагрузкой. Результат анализ нестационарных процессов обычно представляется в виде графика переходного процесса, т.е. зависимости амплитуд колебаний элементов системы от времени. В результате расчета можно оценить время переходного процесса, максимальные и установившиеся значения исследуемых параметров, коэффициент демпфирования системы и т.д.
При исследовании поведения изделия при вынужденных колебаниях (или реакции на периодическое внешнее воздействие) результат обычно представляется в виде графиков зависимости амплитуды колебаний (деформаций) элементов конструкции в зависимости от частоты возмущающей нагрузки. Такую зависимость еще называют амплитудно-частотной характеристикой (АЧХ) изделия. Важным результатом такого исследования является определение диапазона опасных частот внешнего воздействия, при которых происходит наступление резонанса.
Например, на рисунке 4.2.16 приведены амплитудно-частотные характеристики механической системы, построенные для точек (точнее, узлов) 1 и 2. Из анализа графиков можно заключить, что при статическом нагружении (частота внешнего воздействия равна 0) деформация в точке 1 равна 7 мм, а в точке 2 – 0.9 мм. Зато при частоте внешней возмущающей силы, равной 60 Гц, возникает резонанс, и деформация в точке 1 возрастает до 29 мм, а в точке 2 – до 4.4 мм. Пропорционально возрастают и напряжения, что может привести к поломке системе при частоте возмущающей силы около частоты резонанса. Зато при высоких частотах возмущающей силы (более 300…400 Гц) из-за своей инерционности система не успевает за возмущающей силой и деформация в рассматриваемых точках стремится к нулю.
Собственными (свободными) колебаниями называются колебания, возникающие в системе вследствие внешнего толчка, вызывающего первоначальное отклонение, и продолжающиеся затем благодаря внутренним упругим силам, восстанавливающих равновесие. Период (частота) собственных колебаний зависит от формы и упругих свойств системы. В процессе колебаний пространственная система может принимать различные формы, которые называются собственными формами. Таких частот (мод), в принципе, бесконечное количество, но при колебаниях реальной конструкции обычно возникают только несколько первых (старших), причем наибольшая энергия колебаний сосредоточена на первой собственной частоте. Сравнение значений собственных частот и вероятных частот внешней возмущающей силы позволяет избежать возникновения резонансных колебаний в конструкции, заранее принять меры по снижению вибраций.
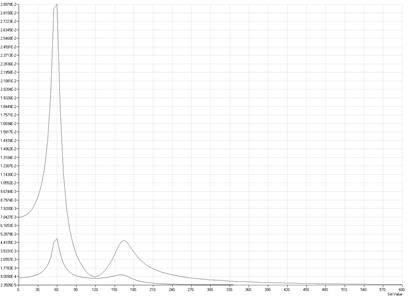
Рисунок 4.2.16 – Зависимость амплитуды колебаний различных частей конструкции в зависимости от частоты возмущающей нагрузки
Анализ форм собственных колебаний позволяет определить те места в конструкции, где деформации при колебаниях будут принимать наибольшие (или наименьшие) значения. Для сложных конструкций это далеко не тривиальная задача, решение которой позволяет существенно снизить наблюдаемый уровень вредных вибраций. Например, на некоторых режимах работы двигателя автомашины могут возникать достаточно мощные низкочастотные колебания, близкие к частоте собственных колебаний кабины машины. Если максимальные амплитуды этих колебаний будут локализоваться в районе педалей (т.е. там, где размещаются ступни водителя), то с точки зрения водителя вибрации будут недопустимо сильные. Но если чуть-чуть изменить конструкцию кабины (например, переместить на несколько миллиметров элементы жесткости), то в районе педалей окажется зона с минимальными амплитудами колебаний. В результате окажется (с точки зрения водителя), что вибрации исчезли.
В некоторых случаях может оказаться полезным наоборот, увеличивать амплитуду вибраций.Известно, что при точении колебания режущей кромки резца в диапазоне частот порядка 200…300 герц помогают образовываться мелкой (дробленной) стружке. Поэтому необходимо ввести резец в режим колебаний на заданной частоте. Для этого, в частности, необходимо, чтобы первая собственная частота резца была равна заданной. Но собственная частота цельного резца порядка нескольких килогерц. Один из самых простых способов снижения собственной частоты системы «резец – резцедержатель» – выполнить прорезь в теле резца. Подбирая расположение и глубину прорези, достаточно просто изменить собственную частоту колебаний части резца в районе режущей кромки с тем, чтобы она соответствовала заданному диапазону.
16. Представление результатов расчета
Результаты расчета можно просмотреть самыми разными путями. Например, самая полная информация о перемещениях, напряжениях и т.д. в каждом узле исследуемого тела записана в текстовом файле результатов. Это не всегда удобно, поскольку такой файл имеет большой размер. Поэтому обычно вначале визуально оценивают распределение расчетных параметров в теле, а затем уточняют значения параметров в элементах с экстремальными значениями.
Раскраска пластины отражает распределение расчетных параметров, в данном случае эквивалентных напряжений по фон Мизесу.Для грубой оценки значений расчетного параметра с правой стороны экрана размещаетсяшкала (т.н. легенда), состоящая изцветных квадратиков. Возле каждого цветного квадратика шкалы стоит соответствующее ему среднее численное значение параметра. Как правило, холодным цветам (фиолетовый, синий, …) соответствует минимальное, а теплым (оранжевый, красный, …) – максимальное значение расчетного параметра.
В некоторых случаях бывает удобно представить результаты распределения расчетных параметров в виде графика зависимости параметра от, например, какой-нибудь координаты. При такой форме представления результатов легко уточнить места расположения экстремальных значений исследуемого параметра.
Следует отметить, что 16-тицветная раскраска в принципе не может позволить оценить точное значение параметра. Цветное изображение предназначено только для качественной оценки распределения исследуемого параметра (например, напряжений). При необходимости уточнить значение параметров, например, напряженно-деформированного состояния, вконкретномконечном элементе достаточно указать на него и получить полный список всех относящихся к нему расчетных параметров.
Следует хотя бы кратко упомянуть об оценке результатов, получаемых при прочностных расчетах. Для оценки напряжений по умолчанию обычно предлагается значения эквивалентных напряжения sЭКВ, вычисленные по энергетической гипотезе фон Мизеса (VonMises Stress):
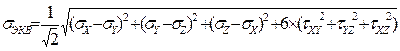
где sX, sY, sZ – нормальные, а tXY, tYZ, tXZ – касательные напряжения. Такой критерий, вытекающий из четвертой теории прочности, наиболее подходит для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию. С другой стороны, для хрупких материалов, для материалов, имеющих разное сопротивление на растяжение и сжатие, для ламинированных материалов, композитов и т.д. может оказаться целесообразным оценивать предельно допустимые напряжения по другим критериям. Например, это могут быть значения наибольших главных напряжений (MajorPrn Stress), допустимые деформации (Translation), максимальные сдвиговые напряжения в верхних волокнах пластины (MaxShear Stress) и т.д. Выбор нужного критерия является важнейшим этапом в оценке результатов расчета и, к сожалению, определяется только знанием и опытом проектировщика.
