III. Общие выводы по результатам проведенного эконометрического анализа

3.1. Характеристика ряда динамики.

3.2. Оценка уравнения Тренда.

3.3. Основная тенденция изменения показателей во времени.

3.4. Прогнозный интервал показателя.

IV. Эконометрический анализ данных на основе регрессионной модели:

4.1. Анализ исходных данных

Построим графики зависимостей x(t), y(t), y(x) (рис. 2 – 4):

Рис. 2 Рис. 3 Рис. 4

Выводы: Графический анализ исходных данных показывает, что для построения модели регрессии может быть использовано уравнение ____ :

y(x) = ____________________ .

4.2. Построение модели регрессии y(x).

В соответствии с методом наименьших квадратов (МНК) для определения параметров ɑ₀ и ɑ₁ решим систему уравнений:

.

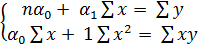Для удобства вычислений параметров системы уравнений составим таблицу

Таблица 4

n	x	y	x2	xy
∑

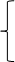Исходя из Таблицы 4, система уравнений с численными значениями параметров имеет вид:

	ɑ0 +		ɑ1 =
	ɑ0 +		ɑ1 =

Решим систему уравнений по правилу Крамера:

D0 =		=		-		=

D1 =		=		-		=

D2 =		=		-		=

_____________ ,

_____________ .

Вывод: Модель регрессии с численными коэффициентами имеет вид:

_______________

4.3. Анализ качества модели регрессии – анализ остатков

Определим остатки по формуле (см. Таблица 5):

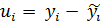
Таблица 5

t	xi	yi			ui – ui-1	(ui – ui-1)2	ui2
∑

Вычислим коэффициент Дарбина-Уотсона dr (промежуточные вычисления выполнены в Таблице 5):

____________ ≈ _______ .

Коэффициент dr является критерием проверки гипотезы о наличии автокорреляции в остатках генеральной совокупности. По таблице Дарбина-Уотсона находим для заданного уровня значимости ɑ = 0,05 и числа наблюдений n = теоритические значения d_L = __________________________ и d_u = _______ .

Для сравнения табличных и расчетных значений построим схему:

Присутствует автокорр. «+»

Зона неопределен-ности

Автокорр. отсутствует

Зона неопределен-ности

Присутствует автокорр. «-»

dL

du

4-du

4-dL

Рис. 5

Вывод: Критерий Дарбина-Уотсона dr = __ ? подтверждает гипотезу о автокорреляции в остатках, поскольку:

< dr <

4.4. Корреляционный анализ данных.

Рассчитаем линейный коэффициент корреляции по формуле:

.

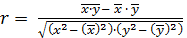Выполним промежуточные вычисления (Таблица 6).

Таблица 6

n	x	y	x∙y	x2	y2
∑
Среднее значение

Величина линейного коэффициента корреляции равна:

_______________________________ .

Вывод: Величина коэффициента корреляции r_xy = ____ свидетельствует

о _________________ __________________ связи между показателями x и y.

^{(направление связи) (сила связи)}

Выполним проверку статистической значимости линейного коэффициента корреляции с помощью критерия Стьюдента (t – статистики):

__________ .

Табличное значение критерия Стьюдента определим, используя группу функций «Статистические», функция СТЬЮДРАСПОБР (для MS Excel – 207; в зависимости от года MS Excel название функции может немного меняться).

t_табл. (ɑ = 0,005; n-k-1 = ___) = _________ .

где ɑ = 0,05 – уровень значимости, n – число заданных значений y;

k – количество независимых переменных (х) в уравнении регрессии.

Сравним t_расч. и t_табл.: t_расч. ___ t_табл.

Вывод: Проверка статистической значимости линейного коэффициента корреляции r_xy показывает, что коэффициент значимо отличается от нуля.

Общий вывод: Корреляционный анализ показал, что между показателями x и y имеется __________________ взаимосвязь.

4.5. Статистический анализ параметров уравнения регрессии.

Проверку статистической значимости парметров уравнения регрессии выполним с помощью критерия Стьюдента (t – статистики).

Рассчитаем значения t – статистики t_расч. и сравним с t_табл.

______________ .

.

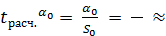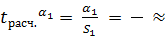t_табл. (ɑ, n-2) = t_табл. (0,05; ___) = .

___ t_табл.

Вывод:Параметр уравнения регрессии ɑ₀ статистически ___ значим, поэтому его следует __ в модели. Параметр уравнения регрессии ɑ1 статистически ___ значим, следовательно, фактор x оказывает статистически ___ значимое воздействие на изменение y. Его следует _____________ в модели.

4.6. Оценка качества модели в целом по коэффициенту детерминации.

1) Определим коэффициент детерминации: .

Для упрощения расчетов составим Таблицу 7.

Таблица 7

t	x	y		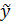	u2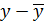
∑

Среднее значение показателя: ________

________________ ≈ .

Вывод: На ___% вариация признаков y (________________________ ) объясняется влияние фактора х (_____________________________________________ ).

2) Оценим статистическую значимость R².

Проверяем нулевую гипотезу о том, что коэффициент детерминации в генеральной совокупности равен нулю. Проверку гипотезы осуществляем с помощью F – критерия (критерия Фишера). Для k = 1 – число факторов в модели:

________________ ≈ _________ .

F_табл. (ɑ, n-k-1, k) = t_табл. (0,05; ___; ___) = ____ .

_____ F_табл. (ɑ, n-k-1, k).

Вывод: Проверка статистической значимости коэффициента детерминации R² показывает, что R² ___ значимо отличается от нуля. Нулевая гипотеза ___ отклоняется с заданным уровнем доверительной вероятности ɑ = 0,05.

Общий вывод: Построенная для прогноза регрессионная модель ____ адекватна.