ИДЗ по теме «Вычисление сводных характеристик выборки. Проверка статистических гипотез»

ИДЗ по теме «Вычисление сводных характеристик выборки. Проверка статистических гипотез»

На опыте было получено 200 значений одного и того же признака, что составило выборочную совокупность.

Номера значений признака	Значения признака, полученные на опыте
1 – 10
11 – 20
21 – 30
37 – 40
41 – 50
51 – 60
61 – 70
71 – 80
81 – 90
91 – 100
101 – 110
111 - 120
121 – 130
131 – 140
141 – 150
151 – 160
161 -170
171 – 180
181 – 190
191 – 200

1. Составить распределение равноотстоящих вариант, разбив всю совокупность на 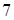интервалов, используя 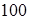данных из 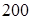предложенных (согласно номера варианта).

2. Построить полигон и гистограмму частот.

3. Методом произведений найти .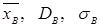

4. Методом сумм найти .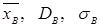

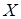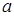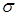5. Считая, что выбранные данные взяты из нормально распределенной генеральной совокупности с неизвестными параметрами и , найти:

а) методом моментов точечные оценки неизвестных параметров 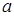и 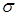нормального распределения;

б) методом наибольшего правдоподобия точечные оценки параметров 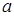и 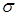нормального распределения, плотность которого 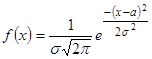(указание: составить и решить систему ).

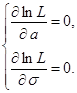6. Считая, что выборочные 100 данных взяты из нормально распределенной генеральной совокупности 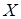, определите доверительные интервалы для оценки неизвестного математического ожидания 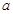генеральной совокупности с заданной надежностью 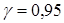, используя полученные Вами значения 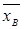и .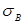

7. Построить нормальную кривую по полученному распределению. Найти асимметрию и эксцесс эмпирического распределения.

8. Используя критерий Пирсона, при уровне значимости а) 0,05;

б) 0,01

проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности 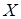с эмпирическим распределением выборки объема .

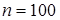Вариант	Номера значений признака	Вариант	Номера значений признака
	1 – 100		41 – 90, 141 – 190
	11 – 110		51 – 100, 151 – 200
	21 – 120		31 – 50, 101 – 180
	31 – 130		41 – 60, 121 – 200
	41 – 140		51 – 70, 11 – 190
	51 – 150		21 – 50, 101 – 170
	61 – 160		31 – 60, 111 – 180
	71 – 170		41 – 70, 121 – 190
	81 – 180		51 – 80, 131 – 200
	91 – 190		61 – 90, 111 – 180
	101 – 200		71 – 100, 121 – 190
	1 – 50, 101 – 150		81 – 110, 131 – 200
	11 – 60, 11 – 160		21 – 60, 111 – 170
	21 – 80, 121 – 150		31 – 70, 121 – 180
	1 – 50, 131 – 180		41 – 80, 131 – 190

Базовый уровень

Тема 52. Генеральная и выборочная совокупности, их характеристики.

1. Дайте определение генеральной и выборочной совокупностей. Назовите основные характеристики генеральной и выборочной совокупности.

Выборочной совокупностьюили простовыборкойназывают совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность объектов, из которых производится выборка.

2. Что такое объём выборки, объём генеральной совокупности?

Объемом совокупности(выборочной или генеральной) называют число объектов этой совокупности.

Например, если из 1000 деталей отобрано 100 деталей, то объем генеральной совокупности N=1000, а объем выборки n=100.

3. Как построить полигон и гистограмму частот?

Пусть из генеральной совокупности извлечена выборка, причем наблюдалось:

x_1- n ₁ раз_;

х_2- n₂ раза;

…

х_к- n_к раз.

и n₁₊ n_2+….n_к=n-объем выборки.

Наблюдаемые значения х_1,х_2….,х_к – называют вариантами, а последовательность вариант, записанная в возрастающем порядке – вариационным рядом.

Числа наблюдений n_1,n_2,…,n_{к –} называют частотами, а их отношения к объему выборки 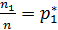, ,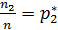….., 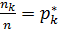относительными частотами.

Причем

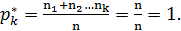
Для графического изображения статистического распределения используют полигоны и гистограммы. Для построения полигонана оси Ох откладывают значения x_i, а на оси Оу – значения частот n_i(относительных частот pi^*).

Пример:

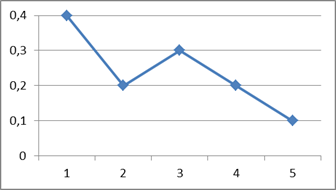
xi
Pi*	0,4	0,2	0,3	0,1

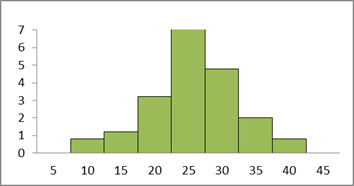
Полигоны используют в случае небольшого количества вариант. В случае большого количества вариант и в случае непрерывного распределения признака чаще строят гистограммы. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала n_i – сумму частот вариант, попавших в i-ый интервал. Затем на этих интервалах как на основаниях строят прямоугольники с высотами .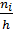

Линейная регрессия

Пусть задана система случайных величин Х и Y, и пусть случайные величины Х и Y зависимы.

Представим одну из случайных величин как линейную функцию другой случайной величины Х:

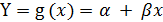, (2.6)

где α, β – параметры, которые подлежат определению.

В общем случае эти параметры могут быть определены различными способами, наиболее часто используются методом наименьших квадратов (МНК).

Функцию 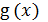называют наилучшим приближением в смысле МНК если математическое ожидание 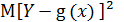принимает наименьшее возможное значение.

В этом случае функцию 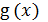называют среднеквадратической регрессией Y на Х. Можно доказать, что линейная среднеквадратическая регрессия имеет вид:

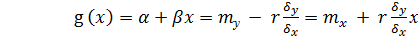, (2.7)

где 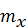, 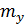– математические ожидания случайных величин Х, Y соответственно;

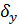, - среднеквадратические отклонения случайных величин Х, Y соответственно;

r – коэффициент парной корреляции, который определяется:

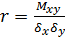(2.8)

где 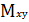– ковариация

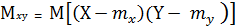(2.9)

Тогда 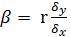- коэффициент регрессии.

4. Отыскание параметров выборочного уравнения прямой линии среднеквадратической регрессии по несгруппированным данным.

Рассмотрим определение параметров выбранного уравнения прямой линии среднеквадратической регрессии по не сгруппированным данным. Пусть изучается система количественных признаков (Х,Y), т.е. ведутся наблюдения за двумерной случайной величиной (Х,Y).Пусть в результате n наблюдений получено n пар чисел .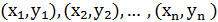

Требуется по полученным данным найти выборочное уравнение прямой линии среднеквадратической регрессии:

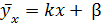
Поскольку данные не сгруппированные, т.е. каждая пара чисел встречается один раз, то можно перейти от условной средней к переменной у. Угловой коэффициент kобозначим через 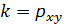и назовем его выборочной оценкой коэффициента регрессии .

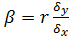Итак, требуется найти:

(2.10)

Очевидно, параметры 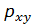и b нужно подобрать так, чтобы точки 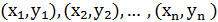, построенные по исходным данным, лежали как можно ближе к прямой (2.10) см. рис. 2.1.

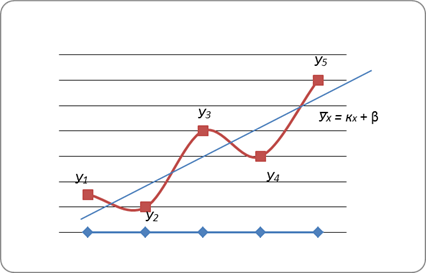
Уточним смысл этого требования. Для этого введем следующее понятие. Назовем отклонением разность вида: ,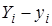

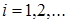
Подберем параметры 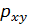и b так, чтобы сумма квадратов указанных отклонений была наименьшей:

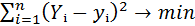
В этом состоит требование метода наименьших квадратов (МНК).

Эта сумма есть функция F отыскиваемых параметров pху и b

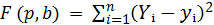
или

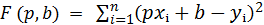
Дляотыскания min найдем частные производные и приравняем к нулю:

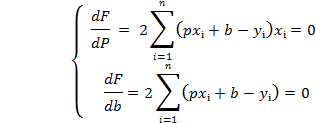
Далее:

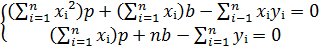
Для простоты вместо 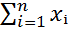будем писать 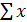(индекс i – опускаем), тогда:

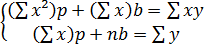
Получили систему двух линейных уравнений относительно p и b.

Решая эту систему получим:

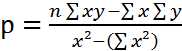(2.11)

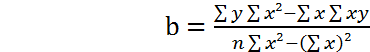
Повышенный уровень

Тема 52. Генеральная и выборочная совокупности, их характеристики.

1. Расскажите, в каком случае лучше строить гистограмму, а в каком случае полигон?

Гистограмма - интервалы, а полигон – точки.

2. Объясните, как получить на основе статистических данных распределение с равноотстоящими вариантами.

ИДЗ по теме «Вычисление сводных характеристик выборки. Проверка статистических гипотез»

На опыте было получено 200 значений одного и того же признака, что составило выборочную совокупность.

Номера значений признака	Значения признака, полученные на опыте
1 – 10
11 – 20
21 – 30
37 – 40
41 – 50
51 – 60
61 – 70
71 – 80
81 – 90
91 – 100
101 – 110
111 - 120
121 – 130
131 – 140
141 – 150
151 – 160
161 -170
171 – 180
181 – 190
191 – 200

1. Составить распределение равноотстоящих вариант, разбив всю совокупность на 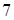интервалов, используя 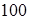данных из 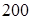предложенных (согласно номера варианта).

2. Построить полигон и гистограмму частот.

3. Методом произведений найти .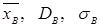

4. Методом сумм найти .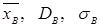

5. Считая, что выбранные данные взяты из нормально распределенной генеральной совокупности 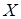с неизвестными параметрам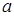и и 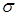, найти:

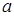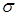а) методом моментов точечные оценки неизвестных параметров и нормального распределения;

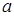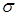б) методом наибольшего правдоподобия точечные оценки параметров и нормального распределения, плотность которого 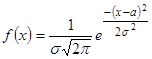(указание: составить и решить систему ).

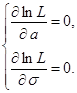6. Считая, что выборочные 100 данных взяты из нормально распределенной генеральной совокупности 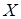, определите доверительные интервалы для оценки неизвестного математического ожидания 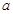генеральной совокупности с заданной надежностью 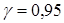, используя полученные Вами значения 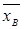и .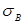

7. Построить нормальную кривую по полученному распределению. Найти асимметрию и эксцесс эмпирического распределения.

8. Используя критерий Пирсона, при уровне значимости а) 0,05;

б) 0,01

проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности 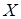с эмпирическим распределением выборки объема .

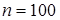Вариант	Номера значений признака	Вариант	Номера значений признака
	1 – 100		41 – 90, 141 – 190
	11 – 110		51 – 100, 151 – 200
	21 – 120		31 – 50, 101 – 180
	31 – 130		41 – 60, 121 – 200
	41 – 140		51 – 70, 11 – 190
	51 – 150		21 – 50, 101 – 170
	61 – 160		31 – 60, 111 – 180
	71 – 170		41 – 70, 121 – 190
	81 – 180		51 – 80, 131 – 200
	91 – 190		61 – 90, 111 – 180
	101 – 200		71 – 100, 121 – 190
	1 – 50, 101 – 150		81 – 110, 131 – 200
	11 – 60, 11 – 160		21 – 60, 111 – 170
	21 – 80, 121 – 150		31 – 70, 121 – 180
	1 – 50, 131 – 180		41 – 80, 131 – 190

Базовый уровень

Тема 52. Генеральная и выборочная совокупности, их характеристики.

1. Дайте определение генеральной и выборочной совокупностей. Назовите основные характеристики генеральной и выборочной совокупности.

Выборочной совокупностьюили простовыборкойназывают совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность объектов, из которых производится выборка.

2. Что такое объём выборки, объём генеральной совокупности?

Объемом совокупности(выборочной или генеральной) называют число объектов этой совокупности.

Например, если из 1000 деталей отобрано 100 деталей, то объем генеральной совокупности N=1000, а объем выборки n=100.

3. Как построить полигон и гистограмму частот?

Пусть из генеральной совокупности извлечена выборка, причем наблюдалось:

x_1- n ₁ раз_;

х_2- n₂ раза;

…

х_к- n_к раз.

и n₁₊ n_2+….n_к=n-объем выборки.

Наблюдаемые значения х_1,х_2….,х_к – называют вариантами, а последовательность вариант, записанная в возрастающем порядке – вариационным рядом.

Числа наблюдений n_1,n_2,…,n_{к –} называют частотами, а их отношения к объему выборки 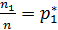, ,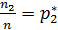….., 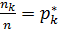относительными частотами.

Причем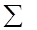

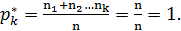
Для графического изображения статистического распределения используют полигоны и гистограммы. Для построения полигонана оси Ох откладывают значения x_i, а на оси Оу – значения частот n_i(относительных частот pi^*).

Пример:

xi
Pi*	0,4	0,2	0,3	0,1

Полигоны используют в случае небольшого количества вариант. В случае большого количества вариант и в случае непрерывного распределения признака чаще строят гистограммы. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала n_i – сумму частот вариант, попавших в i-ый интервал. Затем на этих интервалах как на основаниях строят прямоугольники с высотами 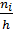.