Сформулировать определение логического следования. Доказать правила следования.

Логическое следование – это отношение, существующее между посылками и обоснованно выводимыми из них заключениями. Логическое следование относится к числу фундаментальных, исходных понятий логики, которую нередко характеризуют как науку о том, "что из чего следует".

Будучи исходным, понятие логического следования не допускает точного определения. В частности, описание его с помощью слов "видимо", "вытекает" и т.п. содержит неявный круг, поскольку последние являются синонимами слова "следует". Понятие следования обычно характеризуется путем указания его связей с другими логическими понятиями, и прежде всего с понятиями логического закона и модели.

Из высказывания А логически следует высказывание В, когда импликация "если А, то В" является частным случаем закона логики.

Важнейшие правила следования

Связь отношения логического следования с общезначимостью.

Th 1. 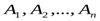╞В, тогда и только тогда, когда ╞ .

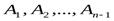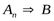В частности, А╞В тогда и только тогда, когда ╞ .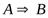

Это утверждение доказывается методом от противного.

Следствие 1. 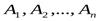╞В, тогда и только тогда, когда ╞ .

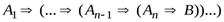Следствие 2. 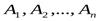╞В, тогда и только тогда, когда 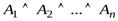╞В.

Применяя к этому следствию Th,получим:

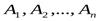╞В тогда и только тогда, когда ╞ .

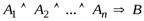Th 2.а) ╞ .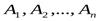

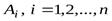б) Если ╞ …, ╞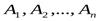

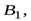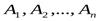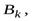
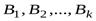╞С ,

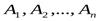то ╞С.

Для сокращения записей обозначим Г любое множество формул, возможно пустое. Тогда первую Th можно сформулировать так:

Г, А╞В тогда и только тогда, когда Г ╞ .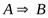

Th 3.а)ЕслиГ, А╞ С иГ, В╞ С, тоГ, АÚВ╞ С.

б) ЕслиГ╞ АÚВ иГ, А╞ С иГ, В╞ С, то Г╞ С.

в) Если Г, А╞ В иГ, А╞ В, то иГ ╞ А.

□ а)Пусть Г, А╞ С (*), иГ, В╞ С (**),

н оГ, АÚВ╞ С.

Тогда существует набор значений атомов, входящих хотя бы в одну из формул множества ГÈ{A, В, С}, при котором все формулы множества ГÈ{A, В} имеют значение И, а формула С — значение Л.

Н о если при некотором наборе формулаАÚВ имеет значение И, то по определению дизъюнкции значение И имеет хотя бы одна из формул А или В. Если таковой является формула А, то при рассматриваемом наборе все формулы множества ГÈ{A} имеют значение И, а формула С — значение Л, значит

Г, А╞ С., что противоречит условию (*).

Если же значение И имеет формула В, то подобным образом получим противоречие с условием (**).

б), в) доказать самостоятельно. ■

Важнейшие правила следования
Логическая операция	Введение	Удаление
	→	→
	→	→
	→	→
	→	→
	→	→

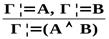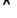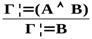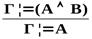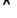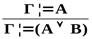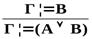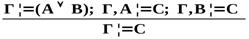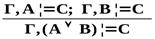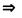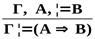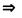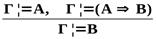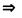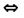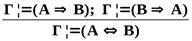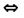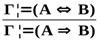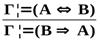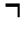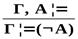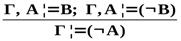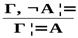Сформулировать определение линейной зависимости векторов.

Определение 1

Пусть имеем систему из n-векторов 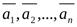и имеем набор чисел 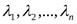_, тогда

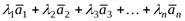(1)

называется линейной комбинацией данной системы векторов с данным набором коэффициентов.

Определение 2(через нулевую линейную комбинацию)

Система векторов 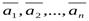называется линейно зависимой, если существует такой набор коэффициентов 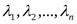, из которых хотя бы один не равен нулю, что линейная комбинация данной системы векторов с этим набором коэффициентов равна нулевому вектору:

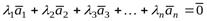.(2)

Пусть 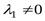, тогда

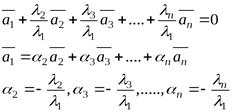
Определение 3 (через представление одного вектора системы в виде линейной комбинации остальных)

Система векторов 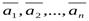называется линейно зависимой, если хотя бы один из векторов этой системы можно представить в виде линейной комбинации остальных векторов этой системы.

Утверждение 1

Определения 2 и 3 эквивалентны.