Дать определение квантификация многоместных высказывательных форм. Сформулировать правила построения отрицания предложений, содержащих кванторы.
Кванторы применяются для того, чтобы перейти от высказывательной формы к истинному высказыванию, эта операция называется квантификацией.
Квантификация - переход от высказывательной формы к истинному высказыванию.
Рассмотрим двуместную высказывательную форму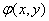 
и всевозможные варианты её квантификации:
(1) 
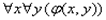
(2) 
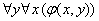
(3) 
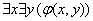
(4) 
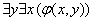
(5) 
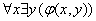
(6) 
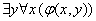
(7) 
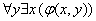
(8) 
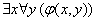
(1) ≡ (2)
(3) ≡ (4)
Одноименные кванторы можно менять местами
(6) => (5)
(8) => (7)
Если высказывательная форма зависит от n переменных, то при квантификации высказывательной формы по xi переменной, xi переменная становится связанной (связана квантором), при этом все остальные называются свободными.
Чтобы перейти от высказывательной формы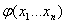 
к истинному высказыванию нужно проквантифицировать её n раз по каждой переменной.
Отрицание предложений кванторами.
Рассмотрим такой пример: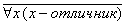 
(отрицание предложения необходимо начинать со слов <неверно, что:>) - <неверно, что все ученики отличники>. Попытаемся перефразировать: <среди учеников есть хотя бы неотличник> или 
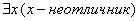, т. е. 
≡ 
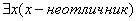. Ещё один пример: 
≡ 
.
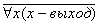Правила построения отрицания предложения с кванторами:
- каждый квантор меняем на противоположный;
- отрицание переносим на высказывательную форму.
Пример: Предложение: <в каждой стране найдётся город, у всех жителей которого глаза одинакового цвета>.
Запись кванторами: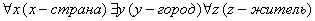 
(глаза одинакового цвета)
Отрицание кванторами: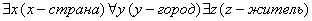 
(неверно, что глаза одинакового цвета)
Отрицание предложение: <существует страна, в каждом городе которой найдётся житель с глазами разного цвета>.
Дать определение кванторов, свободных и связанных переменных.
Кванторы – логические символы или специальные обозначения для некоторых часто встречающихся выражений.
Например: 1) Квантор общности –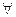 
– любой, каков бы ни был.
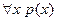– для всех x истинно (или выполнимо) свойство p(x).
2) Квантор существования –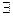 
– существует.
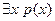– найдутся (или существуют) x, обладающие свойством p(x).
Свободные и связанные переменные
Множество свободных переменных* формулы F определяется рекурсивно, следующим образом:
Определение 1 (Свободные переменные).
- Все переменные, входящие в атомарную формулу, являются свободными переменными этой формулы,
- свободные переменные формулы F являются свободными переменными формулы F,
- переменные, являющиеся свободными для хотя бы одной из формул F или G, являются свободными переменными формулы (F G),
- все свободные переменные формулы F кроме v являются свободными переменными формулы Kv F.
Определение 2 (Замкнутая формула).Формула без свободных переменных называется замкнутой формулой, или предложением.
Определение 3 (Связаная переменная).Переменная v связана в формуле F, если F содержит вхождение Kv, где K – квантор.