Волшебные и магические квадраты

Теперь самое время провести различие: есть два вида квадратов, которые можно условно назвать «волшебными» и «магическими».

Волшебные квадраты — это вид «развлекательной математики», что- то вроде кроссвордов для поклонников данной науки. Они называются «волшебными», поскольку позволяют жонглировать числами путем самых невероятных комбинаций. Хотя их самые ранние версии имели метафизическую подоплеку, для большей части исторических или современных волшебных квадратов не существует мистических ассоциаций. Они просто не предназначены для этих целей, равно как и кроссворды не могут являться путеводной нитью для Хроник Акаши [12].

Квадраты второго типа, настоящие магические квадраты, схожи с первыми своей математической составляющей, но, кроме того, они имеют очень древние корни и долгую историю магического и оккультного использования. Вот о магических квадратах и поговорим далее.

Квадрат Дюрера (почти квадрат Юпитера)

Среди множества людей, очарованных волшебными/магическими квадратами, были художник Альбрехт Дюрер (1471-1528) и американский политик Бенджамин Франклин (1706-1790). Франклин, служивший в конце 1730-х, задолго до своего политического взлета, секретарем в Пенсильванской ассамблее, скуки ради занимался составлением квадратов [13]. Хотя оба, вероятно, наслаждались этими головоломками, Франклин (который был масоном) и Дюрер, конечно же, интересовались и метафизическими аспектами.

Квадрат Юпитера появляется на гравюре Дюрера «Меланхолия» — или почти появляется, поскольку Дюрер позволил себе здесь некоторые вольности (рис. 25, 26, 27). Зачем использовать квадрат Юпитера, если меланхолия метафизически соответствует планете Сатурн? Быть может, исцеления ради, Юпитер (он же Иов, как в слове «веселый» [14]) должен был противодействовать «сатурнальной» угрюмости?

Картина «Меланхолия» наполнена оккультными ассоциациями, над которыми до сих пор бьются историки искусств: сложное геометрическое тело, лестница в семь ступеней, компас (показывающий 5Г25' — значение, используемое для создания семиконечной звезды или разделения круга на 7) и другие реквизиты (рис. 25). Известно, что Дюреру нравилось создавать визуальные головоломки, чтобы с их помощью испытывать и забавлять своих друзей. Вероятно, и «Меланхолия» стоит в том же ряду.

Его решение развернуть квадрат Юпитера на 180° (рис. 26, 27), возможно, было обусловлено спецификой процесса печати. Работавшие в технике гравюры художники, для получения нормального оттиска с вытравленного на пластине изображения, должны были создавать свои композиции в зеркальном виде. Это означает, что любой текст и числа должны были быть первоначально написаны наоборот. Быть может, работая над размещением чисел на гравировальной доске, Дюрер захотел увековечить дату создания картины? Таким образом, повернув традиционный квадрат, он получил искомый 1514 год, прописавшийся в нижнем ряду. Есть еще одна числовая комбинация, о которой Дюрер, безусловно, знал: каждая строка

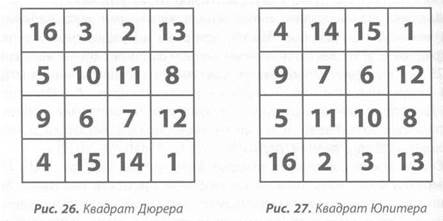квадрата Юпитера при сложении дает 34, а в 1514 году Альбрехту Дюреру исполнилось тридцать четыре года.

Мы используем квадрат Дюрера для исследования возможностей некоторых квадратов — волшебных или магических. В квадрате 4-го порядка имеется шестнадцать ячеек, содержащих числа от 1 до 16. Принципиальным моментом здесь является местоположение каждого числа.

Игры с математикой квадрата Юпитера

Рисунок 28 демонстрирует математику квадрата Юпитера.

. А, В и С. Строки, столбцы и диагонали, как в квадрате Сатурна. Каждое из этих сочетаний в сумме дает 34.

• D. То же происходит и с четырьмя углами: 16+13 + 4+1 =34, и

• Е. С четырьмя центральными ячейками: 10 + 11 + 6 + 7 = 34.

• F. И даже с парами внутренних чисел, расположенных вдоль внешних краев:

3 + 2 + 15 + 14 (вдоль верхнего и нижнего края) = 34 5 + 9 + 8 + 12 (вдоль левого и правого края) = 34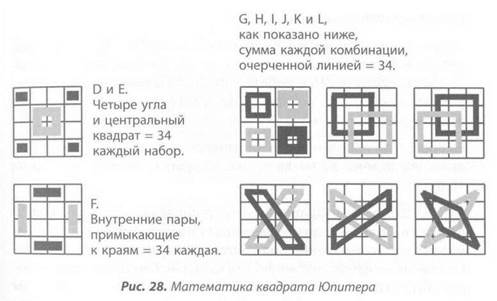

Итак, вот уже четырнадцать различных способов сложения до 34, возможных в этом квадрате, но есть и другие.

G, Н, I, J, К и L показывают еще четырнадцать способов достижения 34 путем сложения конкретных клеток в квадрате Юпитера [15], и этих способов может быть даже еще больше. Если А, В и С работают во всех планетарных квадратах, то многие из этих вариантов присущи именно данному квадрату. Есть свои хитрости и у других квадратов. Я оставляю за вами право их обнаружения, если, конечно, эта логическая игра захватывает ваше воображение.

Если же вы жаждете более детального и углубленного математического анализа, то обратитесь к соответствующей литературе, представленной в конце книги в библиографии.

Теперь давайте вернемся к мистике.

Планетарные квадраты

Здесь они показаны в порядке возрастания, от меньшего к большему. Важно понимать, что сила воздействия от использования этих квадратов зависит не от бездумного копирования их внешнего вида; она заключена в самом акте их созидания с нуля, в последовательной записи одного числа за другим. Когда вы рисуете свой собственный квадрат, используйте последовательность нумерации для медитации. Вписывайте каждое число в квадрат по очереди — 1, 2, 3 и т. д. —- а не просто строчите их ряд за рядом. Совет: сначала пишите цифры карандашом, а затем, обводя их ручкой в соответствующем порядке, — от 1 и далее — фокусируйте на них все свое внимание.

Несколько общих замечаний:

Первое: если вы умножите число в центральной ячейке любого квадрата нечетного порядка на число самого порядка, то вы получите общую сумму чисел в любом ряду/столбце квадрата. Например, у Марса квадрат 5-го порядка, а центральное число — 13, отсюда

5 х 13 = 65 [16].

Второе: если порядок квадрата делится на 3, то общая сумма квадрата упрощается до числа 9. Во всех других случаях — до числа Ю (до 1).

Третье: для всех квадратов нечетного порядка — Сатурна, Марса, Венеры и Луны — вначале следует определить центр. Число 1 находится непосредственно под центром квадрата, а его самое большое число — непосредственно над центром. Сам центральный квадрат будет содержать число «центра»: 1-2-3-4-5-6-7-8-9. Если вы определите начальную, центральную и конечную точки, то схема этих квадратов нечетного порядка выявится сама собой.

Квадраты четного порядка — Юпитера, Солнца и Меркурия —начинаются с числа 1 в верхнем правом углу и заканчиваются наибольшим числом в левом нижнем углу. Помимо этого, их последовательности хитрее, во всяком случае, на мой взгляд. Удачи в обнаружении их схем!

Квадрат Сатурна

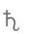
Используется для усиления/улучшения:

• понимания прошлого опыта;

• развития личной дисциплины;

• правильного использования границ и ограничений;

• осмысления кармы.

Для дополнительной информации обратитесь к материалам раздела «Суббота» в главе № 4 [9].

Раскладка квадрата: сетка 3 на 3, квадрат 3-го порядка. Содержащиеся числа: от 1 до 9.

Общая сумма каждой строки, столбца и диагонали: 15. Общая сумма всего квадрата: 45.

Деление общей суммы на число порядка: 45 : 3 = 15.

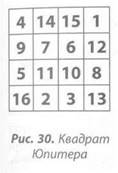Квадрат Юпитера

Используется для усиления/улучшения:

• успеха в судебных делах;

• расширения дела;

• удачи, успеха (и собственного ощущения радости?);

• установления партнерства, союзов;

• духовного роста.

Для дополнительной информации обратитесь к материалам раздела «Четверг» в главе № 4.

Раскладка квадрата: сетка 4 на 4, квадрат 4-го порядка. Содержащиеся числа: от 1 до 16.

Общая сумма каждой строки, столбца и диагонали: 34. Общая сумма всего квадрата: 136.

Деление общей суммы на число порядка: 136 : 4 = 34.

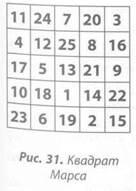Квадрат Марса

Используется для усиления/улучшения:

• принятых решений;

• физической силы, энергии;

• личной храбрости и силы воли;

• контроля темперамента, страстей;

• благословения транспортных средств и механизмов;

• технических способностей;

• коммерческой кулинарии.

Для дополнительной информации обратитесь к материалам раздела «Вторник» в главе № 4.

Раскладка квадрата: сетка 5 на 5, квадрат 5-го порядка. Содержащиеся числа: от 1 до 25.

Общая сумма каждой строки, столбца и диагонали: 65. Общая сумма всего квадрата: 325.

Деление общей суммы на число порядка: 325 : 5 = 65.

Квадрат Солнца

Используется для усиления/улучшения:

• уверенности в себе;

• здоровья, жизненных сил;

• лидерских способностей;

• понимания цели;

• самореализации;

• успеха в новых проектах.

Для дополнительной информации обратитесь к материалам раздела «Воскресенье» в главе № 4.

Раскладка квадрата: сетка 6 на 6, квадрат 6-го порядка. Содержащиеся числа: от 1 до 36.

Общая сумма каждой строки, столбца и диагонали: 1 п Общая сумма всего квадрата: 666.

Деление общей суммы на число порядка: 666 : 6 = 111.

Квадрат Венеры

Используется для усиления/улучшения:

• понимания гармонии и красоты;

• способности к дружбе и любви;

• открытости для радости, игривости и романтики;

• любви и взаимоотношений;

• чувственности;

• домашней кулинарии.

Для дополнительной информации обратитесь к материалам раздела «Пятница» в главе № 4.

Раскладка квадрата: сетка 7 на 7, квадрат 7-го порядка. Содержащиеся числа: от 1 до 49.

Общая сумма каждой строки, столбца и диагонали: 175. Общая сумма всего квадрата: 1225.

Деление общей суммы на число порядка: 1225 : 7 = 175.

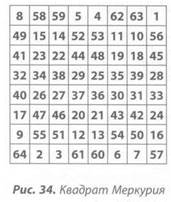Квадрат Меркурия

Используется для усиления/улучшения:

• ясности мышления и восприятия;

• четкости и эффективности общения;

• концентрации, особенно в ходе учебы;

• интеллектуальных стремлений, способностей к приобретению знаний;

• контактов на духовном плане;

• безопасности и своевременности путешествий.

Для дополнительной информации обратитесь к материалам раздела «Среда» в главе № 4.

Раскладка квадрата: сетка 8 на 8, квадрат 8-го порядка. Содержащиеся числа: от 1 до 64.

Общая сумма каждой строки, столбца и диагонали: 260. Общая сумма всего квадрата: 2080.

Деление общей суммы на число порядка: 2080 : 8 = 260.

Используется для усиления/улучшения:

• интуиции и инстинкта;

• фертильности (определенной) и творческих способностей;

• эмоциональной настроенности;

• познаний в области психики;

• всех садовых и фермерских начинаний;

• безопасности путешествий по воде.

Для дополнительной информации обратитесь к материалам раздела «Понедельник» в главе № 4.

Раскладка квадрата: сетка 9 на 9, квадрат 9-го порядка.

Содержащиеся числа: от 1 до 81.

Общая сумма каждой строки, столбца и диагонали: 369.

Общая сумма всего квадрата: 3321.

Деление общей суммы на число порядка:

3321 : 9 = 369.

Использование планетарных квадратов

Выберите планету, традиционная тематика которой соответствует вашим запросам. Например, для улучшения концентрации при подготовке к экзамену логично остановить свой выбор на Меркурии. Открытие нового дела обычно в компетенции Солнца, тогда как усиление товарооборота в уже существующем бизнесе лучше всего обратиться к Юпитеру. Все, что касается ограничений, должно быть адресовано Сатурну. Если же вы желаете благословить и защитить свое новое транспортное средство, то здесь наилучший выбор — Марс.

Одна моя подруга недавно купила дизельную машину, которую она переделала так, что теперь ее можно заправлять использованным растительным маслом. Браво! В качестве воззвания о даровании сохранности машине и ее пассажирам, можно выбрать ключевое слово или коротенькую фразу: «Благослови Мерседес» или «Защити мою машину» или, быть может, «АВС-987», (вымышленный) регистрационный номер. В данном случае подойдет следующее: «Езди хорошо, останься невредимой»[1].

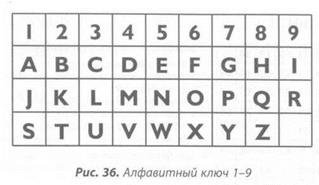
Затем мы ищем числа, соответствующие буквам в выбранной фразе. Наша первая задача состоит в том, чтобы использовать числа от 1 до 9 в качестве ключа для алфавита (рис. 36). Многие из нас, вероятно, Уже знакомы с этим ключом, поскольку он используется в нумерологии и в простом шифровании.

При работе со схемой 1-9 наша фраза будет выглядеть как на рисунке 37.

Если вы используете квадрат Сатурна или вам нужны буквы от Q до Z в квадрате Юпитера, то вам следует применять шифрование 1-9, показанное на рисунке 36.

Однако мы также пользуемся квадратом Марса, квадратом 5-го порядка, с двадцатью пятью отдельными клетками. Поскольку наша фраза не включает Z, двадцать шестую букву, мы можем, вместо того чтобы задействовать одно число из кода 1-9 для трех разных букв, назначить отдельное число для каждой буквы. Дабы воспользоваться уникальными числами прибегните к ключу 1-26, показанному на рисунке 38.

Примечание: если вы упростите каждое двузначное число, этот шифр , _дет соответствовать шифру 1-9 на рисунке 36.

Теперь фраза будет выглядеть как на рисунке 39.

Гематрия

Разбирая побуквенно различные слова, мы иногда встречаем удивительные числовые параллели. Например, lion (лев) выражается в числах как 3-9-6-5; cheetah (гепард) как 3-8-5-5-2-1-8; a tiger (тигр) как 2-9- 7-5-9, если работать с набором простых чисел (см. рис. 36). Давая суммы 23, 32 и 32, все они упрощаются до 5.

Если вы находите такие совпадения интригующими, гематрия может стать вашим любимым занятием. Схожая с приведенным примером, но куда более сложная гематрия основывается на двадцати двух буквах древнееврейского алфавита и еще пяти буквах того же алфавита, повторяющихся в несколько отличных формах, когда они исполняют роль окончаний. Итого двадцать семь. Каждой букве присваивается числовое значение, но в отличие от уже виденных нами алфавитов типа A-Z, эти значения зачастую достигают куда более значительных величин — вплоть до трехзначных — так что когда слово записывается подобным образом, сумма может быть внушительной. Другие отличия: в гематрии суммы не упрощаются до однозначных чисел; у каждой буквы есть также глубокий эзотерический смысл; кроме того, гематрия основывается на иврите, а многие из нас работают на родном языке, поскольку заклинание должно быть фонетическим.

«Каббала называет древнееврейский алфавит „буквами ангелов"». Так написала мадам Блаватская в своей книге «Тайная доктрина» [17], потому использование ивритских букв в гематрии является одним из способов исследования их божественных ассоциаций. Гематрия глубокое, древнее, сложное и тонкое учение — это самое общее определение того, чем оно занимается.

Согласно гематрии, лев, которого мы упоминали ранее, имеет следующее численное значение: 30 + 10 + 70 + 50 = 160. Тогда как гепард {cheetah) выглядит гораздо солиднее: 60 (с/г) + 8 (долгое е) + 300 (t) + 1 (а) = 369.

Для более глубокой интерпретации обратимся к символике гематрии (рис. 40). С ее точки зрения, имя нашего старого знакомца льва (lion) слагается из букв, имеющих следующие метафорические значения: «стимул вола», то есть «прут», «рука», «глаз» и «рыба» [18]. Название буквы ламед, часто переводимое как «стимул вола», в более широком смысле может означать нечто вроде «мотиватора». Йод или «рука», возможно, олицетворяет собой стремление к воплощению своих идей в физическую реальность, то есть, буквально, борьбу с судьбой. Айн или «глаз» подразумевает видение и восприятие, взгляд и понимание. Наконец, Нун или «рыба», должно быть,

говорит о негостеприимной для людей окружающей среде и необходимости адаптации для выживания во враждебном мире. Как видим, посредством этого глубокого толкования понятие «лев» обретает куда более сложное символическое значение.

Название на иврите	Изначальное значение	Буква (англ. алфавит)	Числовое значение
Алеф	Бык	А
Бет	Дом	В
Гимель	Верблюд	C/G
Далет	Дверь	D
Хе	Окно	Е/Н
Вав	Дверная ручка или крючок	St/V
Зайн	Оружие	Z
Хет	Ограда	Долгая E/Ch
Тет	Змея	Th/T
Йод	Рука	I
Каф	Ладонь	К
Ламед	Прут	L	ЗО
Мем	Вода	М
Нун	Рыба	N
Самех	Поддержка	Твердая Ch/S
Айн	Глаз	О
Пе	Рот	Р
Цаде	Рыболовный крючок	Q/Tz
Коф	Затылок	R/Rh/Q
Реш	Голова	S/R
Шин	Зуб	T/Sh
Тау	Крест	Y/U/Th
Каф (конечная)		Ph
Мем (конечная)		Ch
Нун (конечная)		Ps
Пе (конечная)		Долгая 0
Цаде (конечная)		S

Рис. 40. Древнееврейский гематрический код

Жестокий «король джунглей»? Безусловно, но рассмотренные выше характеристики дают много пищи для размышлений и могут служить руководством для человеческих поступков в условиях «джунглей» современной жизни.

Настоящие практики от гематрии будут использовать не только комплекс метафорических значений букв, слагающих имя объекта исследования, но также изучать и числовую составляющую, в данном случае слова «лев». Какие еще слова дают сумму 160? Можно ли с их помощью расширить наше понимание исследуемого слова?

Вавилоняне также использовали ге- матрическую систему. У царя Саргона II

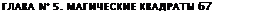
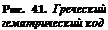
(ок.

ной 16 283 кубита (1 кубит = 0,48 м), построенная на основе числового значения его имени [19]. Этот грандиозный пример может вдохновить нас на самостоятельное использование ге- _матрии, быть может, не для постройки массивных стен, но для куда более скромных измерений и подсчетов, основанных на гематрическом значении собственного имени или качеств, которые мы желали бы заполучить.

Так, если бы я делала талисман, способствующий проявлению ранее упомянутых львиных качеств, я бы украсила его числом 160.

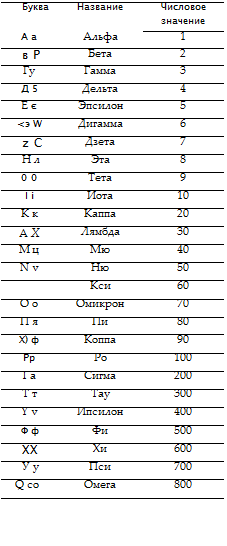
Греческие буквы также имеют числовые значения, и существует собственная традиция их изучения (рис.

41). Например, гностическое божество Абраксас имеет числовое значение 365 (1 + 2 + 100 + 1 + 60 + 1 + 200), равное числу дней в году [20].

В традиционной практике ученые применяют гематрию к священным текстам, выискивая слова с равными числовыми значениями.

Перед первооткрывателем, обнаружившим однажды этот числовой резонанс, может открыться бессчетное количество направлений для исследования. Результат? Тайная гармония, скрытая в паутине взаимосвязей смыслов и совершенно невидимая для случайного читателя того же текста.

Запаситесь терпением: это запросто может оказаться работой на десятилетия.

Неважно, используете вы код с рисунка 36 или с рисунка 38, в любом случае, давайте начинать. Мы собираемся «вписать» фразу «Езди хорошо, останься невредимой» в квадрат Марса (рис. 31), используя числа, которые мы только что подобрали. С этого момента у вас под рукой должны быть калька, линейка и ластик. Для начала проведите «тест-драйв» своей Фразы на кальке, наложенной поверх магического квадрата. Таким образом вы сможете определить, где расположены ваши числа, и избежать ошибок в нарисованном от руки квадрате, над созданием которого вы Долго трудились. Для начала обратитесь к рисунку 42. Как можете убе-

диться, ваша фраза графически имеет, скорее, приятный дизайн, а не выглядит хаотичным клубком. Редактируйте и вновь воспроизводите свой чертеж — вот для чего вам нужны калька и ластик. Рисуйте линии от руки или при помощи линейки, если хотите, чтобы они были совершенно прямыми. Когда потренируетесь на черновике, уберите кальку и, сфокусировавшись на своих стремлениях, проведите линии на самом квадрате.

Рисунок 42. Начало фразы по Марсу: это первые четыре «буквы» (R-u-п w), обозначающиеся числами 18 (со звездочкой), 21, 14 и 23. Ничего обязательного, но запомните, короткие фразы работают лучше, чем словесные нагромождения. На рисунке 43 показывается, как должен выглядеть результат.

Рисунок 43. Конец фразы по Марсу: графическая форма искомой фразы, начало и окончание которой помечены звездочками.

Как правило, создаются и используются квадраты, соответствующие планете, находящейся на тот момент в астрологически благоприятном положении относительно других небесных тел. Можно просто работать в день, связанный с конкретной планетой. Если хотите, очертите круг и определите стороны света перед началом работы.

Экспериментируйте с различными цветами и типами фломастеров, цветных карандашей, экзотической бумаги или чем угодно, что может подстегнуть вашу фантазию. Когда ваш узор будет готов, его можно вырезать или вышить, начертить на водной поверхности или над церемониальным возлиянием. Возможности безграничны. Фиксируйте случаи использования квадратов. Эти записи станут вашим справочником или книгой рецептов для будущего применения. Если что-то работает особенно хорошо, есть смысл вновь и вновь воспроизводить данную процедуру, а в случае неэффективности чего-либо вы можете внести необходимые коррективы.

Что еще можно делать с магическими квадратами

• Определите в каждом квадрате его «магическую линию». Делается это следующим образом: найдя число 1, проведите от него линию к числу 2, затем к числу 3 и так далее, по возрастающей, к конечному числу. В результате, перед вашими глазами предстанут великолепные геометрические узоры, которые могут послужить и вполне практическим целям. Планировка сада? Деловой логотип? Татуировка? Наложенный на выбранную карту маршрут для отпуска?

• Прочертите линию, соединяющую дату и время вашего рождения. Это действие должно способствовать активизации позитивных талантов и потенциала, имеющихся у вас в наличии. Используйте квадрат планеты, которая управляет вашим знаком, или планеты, положение которой вы находите наиболее благоприятным для вашего колдовства, или же проделывайте это с каждым квадратом, а потом сравнивайте результаты. Таким вот образом можно обнаружить порядок линий, который в дальнейшем станет основой личного магического символа.

Лунный лабиринт

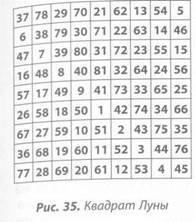
В поисках каких-либо еще магических чудес квадратов я обратилась к замечательной книге Клиффорда А. Пиковера «Дзен магических квадратов, кругов и звезд». Используя магический квадрат 9-го порядка (не квадрат Луны), Пиковер обнаружил интересный геометрический рисунок, получившийся при вымарывании всех нечетных чисел [21]. Я скопировала эту идею, наложив кальку поверх другого квадрата 9-го порядка, настоящего квадрата Луны (рис. 35). Поскольку я использовала другой квадрат, то и получила совершенно иной узор. Потрясенная неожиданным узнаванием, я поняла, что вижу перед собой «семенную диаграмму» — основу для семиоборотного лабиринта (см. рис. 44, 45).

Варианты этого лабиринта обнаружены по всему миру, на пространстве от Крита до юго-запада Америки. Я впервые узнала о «семенной Диаграмме» на семинаре по лабиринтам, где мы создавали большой лабиринт на песчаном берегу горного озера [22]. Она состоит из вертикального + (знак плюса) в центре, четырех уголковых L-образных форм и четырех угловых точек. Эти компоненты скрытно присутствуют в обычном квадрате Луны и становятся видимыми только при вымарывании всех нечетных чисел.

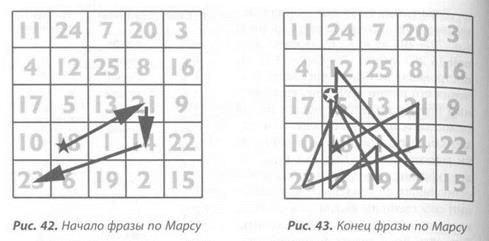
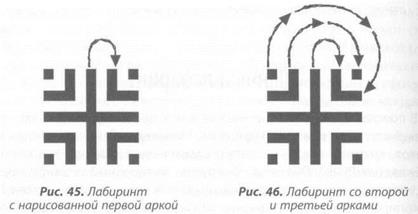
Оставив достаточно места по сторонам, вычертите большую семенную диаграмму на песчаном пляже или нарисуйте маленькую на листе бумаги, а затем приступайте к созданию лабиринта. Соединив верхушку главной вертикальной линии с вершиной правого верхнего L (как показано на рис. 45), продолжайте создавать арки, прочерчи-

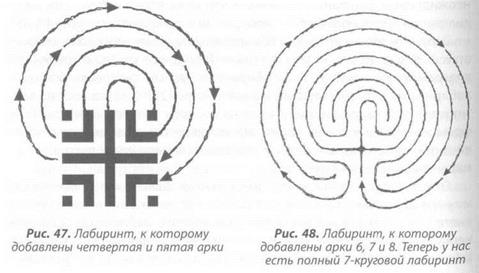_вая линии слева направо, как показано на рисунке 46 и 47. В общем, если вы начали с линии, то закончите точкой и наоборот. Заметьте, что U-образные «углы» разворота, образующие петли лабиринта, являются также внешними углами квадрата Луны.

Как и сама Луна, растущая и убывающая справа налево, двигается по небосводу слева направо, так и вы, будучи в лабиринте, должны перемещаться как посолонь, так и противосолонь. Попробуйте раскрасить созданный на бумаге лабиринт карандашами всех цветов радуги, сменяя один цвет на другой в месте скруглення углов.

Несколько необычных дополнительных замечаний:

Первое: в квадрате Луны 81 ячейка и, соответственно, 81 число, а масса самой Луны составляет 1/81 от массы Земли [23].

Следующее: Земля движется в пространстве со скоростью 28 миль в час; Луна — со скоростью 2268 миль в час. Это означает, что Луна движется в 81 раз быстрее Земли [24].

Последнее: как вырезано на статуях майя в Паленке «81 луна составляет 2392 дня» [25]. Разделите 2392 на 81 и вы получите 29,53 — число, равное количеству дней в лунном цикле, по подсчетам современных ученых.

Глава № 6

Ход конем и коды храмовников?

Одной из замечательных особенностей магических квадратов является их способность служить полем для всякого рода узоров. Это их свойство изящно демонстрирует квадрат Меркурия (8 на 8), сетку которого можно использовать как шахматную доску. В отличие от шахматных фигур, особый интерес для нас представляют кони.

Ход конем

Каждая шахматная фигура имеет свой способ перемещения по доске. Конь [1] ходит буквой «Г» — на две клетки по прямой, неважно, по горизонтали или по вертикали, а затем на одну налево или направо. Этот особенный способ передвижения дает возможность осуществить шахматную хитрость, интригующую игроков и математиков на протяжении нескольких столетий: ход конем.

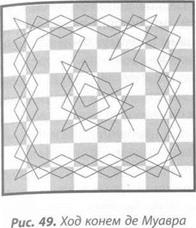
Речь идет не об игре в шахматы. В ходе конем в игре участвует лишь один конь, и ему предстоит совершить большое путешествие по доске. Конь, передвигаясь своим стандартным способом и посещая каждую клетку всего один раз, должен в обязательном порядке побывать на всех клетках доски. Хотя маршруты коня по шахматной доске были известны многим игрокам, первое дошедшее до нас решение дал французский математик Абраам де Муавр (1667-1754). Его последовательность создает узор, который временами смотрится как плетенка, хотя можно заметить, что ее начальная и конечная точки не стыкуются и потому цепочка является разомкнутой (рис. 49).

Другой французский математик Адриен Мари Лежандр (1754-1883) смог найти решение, при котором первая и последняя позиции на доске находились друг от друга в одном прыжке коня, так что цепочка могла быть замкнута или пройдена повторно через финальный ход, возвращающий к исходной клетке. Конь Лежандра хоть и следует более извилистым путем, чем тот, что нашел де Муавр, но узор его маршрута также упорядочен по своей сути. Если вы обратите внимание на рисунки, получающиеся после записи фраз на ваших собственных магических квадратах,

то оцените различие: отображение слов не связано с какими-либо ограничениями или предсказуемостью (рис. 50).

Контрастирующая с вышеназванными вариантами, оригинальная версия хода конем была предложена швейцарским математиком Леонардом Ойлером (1707-1783). Согласно ей конь двигается сначала через одну часть доски, а затем — через другую, за один ход покрывая половину шахматной доски, что делает возможным повторное прохождение, замыкающее цепочку. В ойлеровском узоре — половинка к половинке — есть что-то от «плетенки» де Муавра, но, в любом случае, они совершенно отличны друг от друга [2] (рис. 51).

Вот некоторые из возможных вариантов хода конем, представленные вам для возбуждения интеллектуального аппетита и получения визуального представления о том, как это может выглядеть. Теперь переходим к другим рыцарям, к тамплиерам (храмовникам).