Интегральный метод расчета струи
При решении многих прикладных задач может быть использован интегральный метод расчета струи, предложенный Г.А.Абрамовичем.
Преимущество этого метода заключается в его относительной простоте и наглядности: в ряде случаев расчет струи может выполняться без использования компьютера по алгебраическим формулам, дающим возможность также проводить анализ влияния исходных параметров струи на ее характеристики. Основной недостаток интегрального метода расчета струи заключается в том, что он может быть использован только для расчета течений, поперечные поля которых обладают свойствами подобия и автомодельности. Такие течения называются, соответственно, подобными и автомодельными.
В случае струйных течений под подобием поперечных полей понимается совпадение безразмерных полей одноименных параметров в сходственных течениях нескольких струй, а под автомодельностью – независимость формы безразмерного поля некоторого параметра вдоль оси одной струи. В случае однофазных течений понятия подобия и автомодельности тождественны. Особенностью подобных и автомодельных течений является то, что для описания поперечного поля каждого параметра этих течений необходимо иметь только одно выражение, которое справедливо для любого сечения струи.
Интегральный метод расчета струи основан на использовании законов сохранения массы, количества движения и энергии, записанных для начального и текущего сечений струи, а также в использовании свойств подобия и автомодельности поперечных полей параметров и уравнения, описывающего изменение границ струи. В результате решения интегральных уравнений находятся значения всех параметров на оси струи, по которым с использованием универсальных формул, например формул Шлихтинга, могут быть рассчитаны параметры газа в произвольной точке рассматриваемого сечения струи.
Из опытов известно, что подобие и автомодельность поперечных полей параметров струй наблюдаются не по всей длине струй, а на отдельных их участках. В связи с этим в интегральном методе расчета струя с равномерным распределением параметров в ее начальном сечении делится на три участка (рис. 4.1): начальный, переходный и основной. Начальный участок струи начинается на срезе сопла (в начальном ее сечении) и заканчивается в сечении, в котором струйный пограничный слой, начинающийся на кромке сопла, смыкается на оси струи. Область, лежащая между внутренними границами слоя смешения, называется потенциальным ядром струи или ядром постоянных параметров. На некотором расстоянии от конца начального участка струйное течение приобретает такой же вид как течение газа из точечного источника. Этот участок струи называется основным. Между начальным и основным участками струи располагается переходный участок. В расчетах обычно принимают, что сразу за начальным участком следует основной участок, сопрягающийся с начальным участком в переходном сечении. Подобие и автомодельность поперечных полей одноименных параметров струи наблюдаются только в пределах начального и основного участков и отсутствуют в переходном участке. При этом формулы, описывающие безразмерные поля избыточных параметров струи в начальном и основном ее участках различны.
В основном участке струи безразмерные поля скоростей и температур обычно описываются формулами [2, 8]
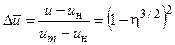 (4.7)
(4.7) 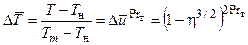 (4.8)
(4.8)
в которых u, Т - скорость и температура в рассматриваемой точке струи, uн , Тн - скорость и температура на границе струи, um, Тm - скорость и температура на оси струи, Prт - турбулентное число Прандтля (для круглой струи Prт = 0,75…0,8), h = r/Rгр - безразмерная координата, r - текущий радиус струи, Rгр - радиус границы струи.
За границу струи принимается значение радиуса струи, на котором параметры газа отличаются на 1% от их значений во внешнем потоке. В интегральном методе расчета принимается, что границы струи по скорости, температуре и концентрации совпадают.
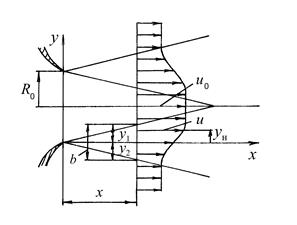 При описании безразмерных полей параметров в начальном участке струи вводится система координат, изображенная на рис. 4.2. В этой системе координат безразмерные поля скоростей и температур газа могут быть описаны формулами [2]
При описании безразмерных полей параметров в начальном участке струи вводится система координат, изображенная на рис. 4.2. В этой системе координат безразмерные поля скоростей и температур газа могут быть описаны формулами [2]
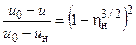 (4.9)
(4.9) 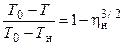 (4.10)
(4.10)
 где u0, Т0 - скорость и температура газа в потенциальном ядре струи, hн - безразмерная координата
где u0, Т0 - скорость и температура газа в потенциальном ядре струи, hн - безразмерная координата
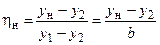 .
.
В последнем выражении: у1 - ордината внутренней границы слоя смешения, у2 - ордината внешней границы слоя смешения, yн - ордината точки в слое смешения со скоростью u, b - ширина слоя смешения.
Формулы (4.7)-(4.10) называются формулами Шлихтинга. Наряду с формулами Шлихтинга для описания безразмерных полей параметров струи могут использоваться и другие формулы, но ими пользуются редко и поэтому они здесь не рассматриваются.
Для расчета параметров газа в произвольной точке слоя смешения начального участка струи с использованием формул (4.9) и (4.10) достаточно знать параметры газа в потенциальном ядре струи и на ее границе. Чтобы рассчитать параметры газа в какой-либо точке основного участка струи, наряду со значением параметров газа во внешней среде (на границе струи) необходимо предварительно определить значения этих параметров на оси струи.
Получим систему уравнений, позволяющую рассчитывать параметры газа на оси основного участка струи. Будем рассматривать дозвуковую неизотермическую (Т0 ¹ Тн) осесимметричную изобарическую струю постоянного состава, имеющую в начальном сечении равномерные поля всех параметров. Изобарической струей называется струя, давление в каждой точке которой постоянно (р=р0=рн). В этом случае система уравнений состоит из уравнения количества движения, энергии и уравнения, описывающего изменение границ струи.
Изменение границы струи в ее основном участке описывается уравнением [1]
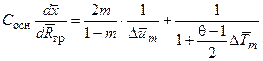 (4.11)
(4.11)
в котором
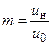 ,
, 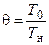 ,
, 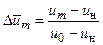 ,
, 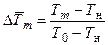 ,
, 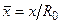 ,
, 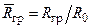
Сосн - константа, для основного участка струи Сосн = 0,22.
Величина т называется коэффициентом спутности, а величина q - начальным подогревом.
Особенность использования законов сохранения в интегральном методе расчета параметров струи заключается в том, что они применяются для избыточного количества рассматриваемой субстанции в струе по отношению к окружающей среде.
Так, уравнение сохранения избыточного количества движения в изобарической струе в общем виде записывается следующим образом [2]
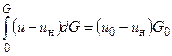
Здесь: G - расход газа, протекающего через произвольное поперечное сечение струи, G0 - расход газа через начальное сечение струи, dG = rudF - расход газа через элемент dF сечения струи.
Для круглой струи
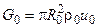 ,
, 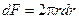
Следовательно, уравнение количества движения можно переписать в виде
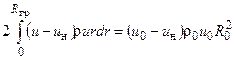
Разделим левую часть этого уравнения на его правую часть
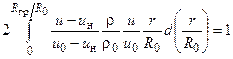
Использование формул
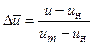 ,
, 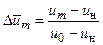 и
и 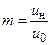
позволяет записать отношение скоростей u/u0 в виде
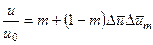
Отношения (u-uн)/(u0-ин) и r/R0, можно записать следующим образом
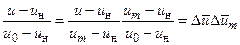 ,
, 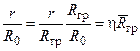
Учитывая, что 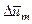 и
и 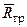 от r не зависят и, вводя обозначения
от r не зависят и, вводя обозначения
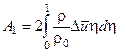 ,
, 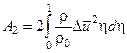 (4.12)
(4.12)
окончательно получаем
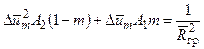 (4.13)
(4.13)
Уравнение сохранения избыточного количества тепла, записанное для основного участка струи, имеет вид [2]
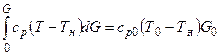
Проведя преобразования этого уравнения по аналогии с преобразованием уравнения количества движения в случае ср= const, имеем
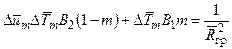 (4.14)
(4.14)
При записи этого уравнения введены обозначения
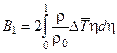 ,
, 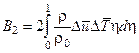 (4.15)
(4.15)
В интегралах (4.12) и (4.15) 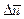 и
и 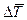 описываются формулами (4.7) и (4.8), а отношение плотностей r/r0 может быть найдено из условия p=p0 с использованием формул
описываются формулами (4.7) и (4.8), а отношение плотностей r/r0 может быть найдено из условия p=p0 с использованием формул 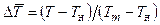 ,
, 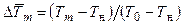 и
и 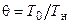 :
:
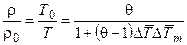
Вместо уравнения (4.14) можно использовать уравнение, связывающее 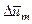 и
и 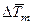 . Это уравнение получается путем деления левой и правой частей уравнения (4.14) на соответствующие части уравнения (4.13):
. Это уравнение получается путем деления левой и правой частей уравнения (4.14) на соответствующие части уравнения (4.13):
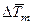 =КТ
=КТ 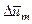 (4.16)
(4.16)
Здесь
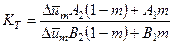 (4.17)
(4.17)
В интегральном методе расчета струи часто предполагается, что коэффициент КТ практически не изменяется по длине струи и слабо зависит от начального подогрева 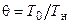 .
.
Решая систему уравнений (4.11), (4.13) и (4.16), можно найти 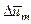 ,
, 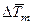 ,
, 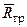 и, следовательно, um, Tm и Rгр, а затем по формулам Шлихтинга (4.7) и (4.8) рассчитать значения u и Т в любой точке основного участка струи.
и, следовательно, um, Tm и Rгр, а затем по формулам Шлихтинга (4.7) и (4.8) рассчитать значения u и Т в любой точке основного участка струи.
В общем случае эта система решается с использованием компьютера. Точное аналитическое решение может быть получено для струи постоянной плотности (r0=rн), когда значения интегралов (4.12) и (4.15) являются постоянными величинами; при Prт =
= 0,75 А1= 0,258, А2 = 0,134, В1= 0,328 и В2= 0,155.
В случае круглой затопленной (uн = 0) неизотермической (q ¹ 1) струи, изменение параметров вдоль оси которой описывается системой уравнений
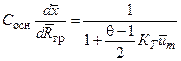 , Сосн = 0,22
, Сосн = 0,22
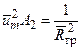 ,
, 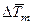 =КТ
=КТ 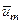 ,
,
можно получить приближенное решение этой системы уравнений. Но полученное решение является громоздким. Для вычисления параметров на оси затопленной неизотермической круглой струи с начальными равномерными полями всех ее параметров при 1 £ q£ 5 можно пользоваться следующим относительно простыми алгебраическими уравнениями [1]:
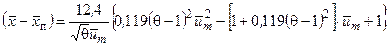 (4.18)
(4.18)
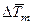 =КТ
=КТ 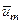 (4.19)
(4.19)
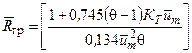 (4.20)
(4.20)
В этих выражениях 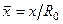 , х - расстояние данного сечения от начального сечения струи, R0 - радиус начального сечения струи (радиус сопла),
, х - расстояние данного сечения от начального сечения струи, R0 - радиус начального сечения струи (радиус сопла), 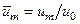 ,
, 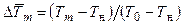 ,
, 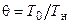 ,
, 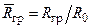 , КТ=А2/В2= 0,745.
, КТ=А2/В2= 0,745.
Абсцисса переходного сечения струи 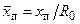 пропорциональна длине ее начального участка
пропорциональна длине ее начального участка 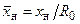 . В первом приближении можно считать, что
. В первом приближении можно считать, что 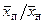 не зависит от m и q и между ними существует зависимость [1]
не зависит от m и q и между ними существует зависимость [1]
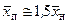 (4.21)
(4.21)
Для вычисления длины начального участка 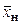 можно использовать формулу [1]
можно использовать формулу [1]
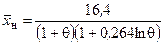 (4.22)
(4.22)
В том случае, если начальные поля параметров струи являются неравномерными, использование формулы (4.22) дает значительную погрешность в вычислении 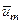 .
.
Расчеты струй с неравномерными полями параметров газа в их начальных сечениях могут проводиться по уравнениям (4.13) и (4.14), если в них ввести коэффициенты, учитывающие эту неравномерность. Но эти расчеты можно выполнить только с использованием компьютера. Для расчета струй, в которых начальные поля скорости газа близки по форме к полю скорости при турбулентном течении газа в трубе, в [9] предложены простые алгебраические уравнения, дающие хорошее согласование расчета с экспериментом
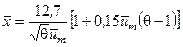 (0 < q < 10) (4.23)
(0 < q < 10) (4.23)
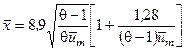 (q > 10) (4.24)
(q > 10) (4.24)
4.2. Лабораторная работа "Теоретическое и экспериментальное исследование турбулентной газовой струи"
Цели работы - получение экспериментальных и теоретических зависимостей 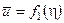 ,
, 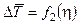 ,
, 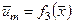 и
и 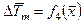 , сопоставление этих зависимостей между собой.
, сопоставление этих зависимостей между собой.
