Лекция 3. Геометрические характеристики плоских сечений стержня.

Математические определения геометрических характеристик плоских фигур: статические моменты, осевые моменты инерции и центробежный, полярный момент инерции. Центральные оси. Главные оси. Определение положения центра тяжести элементарных сечений и составленного из элементарных фигур. Нахождение геометрических характеристик сечений относительно центральных осей.

Различают следующие характеристики сечений: площадь А, статические моменты площади, моменты инерции площади, центробежный момент инерции площади.

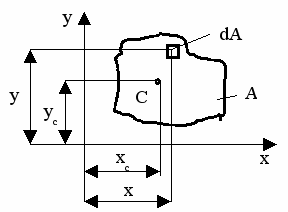
Рис.1

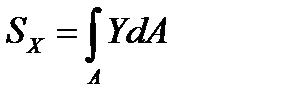
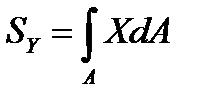Под статическим моментом площади относительно некоторой оси понимается сумма произведений площадей элементарных площадок на расстояния от их центра тяжести до соответствующей оси:

Определение центра тяжести сечения. Статические моменты сечения относительно осей проходящих через центр тяжести равны нулю, поэтому их используют для определения координат центров тяжести сечения. Для этого проводят вспомогательные оси x и y и координаты центра тяжести сечения определяют по зависимостям:

.

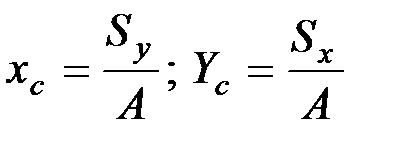Моменты инерции сечения. Осевым моментом инерции сечения называется интеграл по площади произведения элементарной площадки на квадрат расстояния до оси. Осевые моменты инерции сечения относительно осей x и y будут соответственно равны

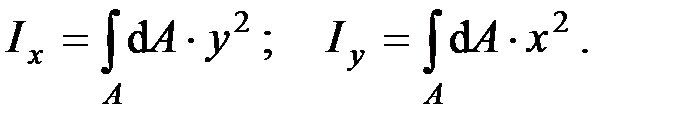(1)

Полярным моментом инерции сечения 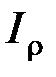называется интеграл по площади произведения элементарной площадки на квадрат расстояния до начало координат.

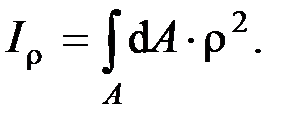
Учитывая, что , получаем

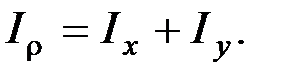
Полярный момент инерции сечения равен сумме осевых моментов инерции сечения.

Оси, относительно которых центробежный момент инерции равен нулю, называются главными центральными осями, осевые моменты инерции относительно их принимают свои экстремальные значения (максимум и минимум).

Полярный момент инерции

.

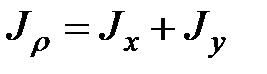
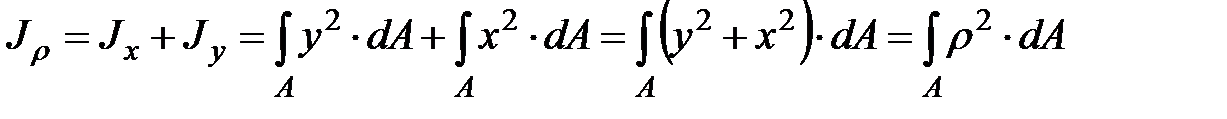Полярный момент инерции относительно данной точки – сумма произведений элементарных площадей dA на квадраты их расстояний ( 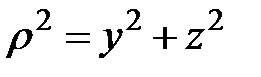) до этой точки, взятая по всей площади сечения А.

Моменты сопротивления

Осевой момент сопротивления относительно рассматриваемой оси – величина равная моменту инерции относительно той же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки

; .

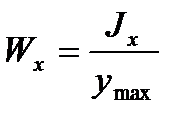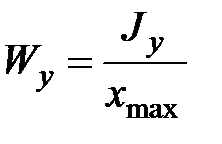Полярный момент сопротивления

Вычисление геометрических характеристик простых фигур

Прямоугольное сечение.

Определим осевой момент инерции прямоугольника относительно оси х.

Разобьем площадь прямоугольника на элементарные площадки с размерами b (ширина) и dy (высота) (рис.2). Тогда площадь такого элементарного прямоугольника (заштрихована) равна . Подставляя значение dA в формулу для определения осевого момента инерции, получим:

Рис.2

По аналогии запишем

.

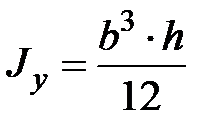d

z

y

D

Рис.3

Круглое сечение

Вначале целесообразно найти полярный момент инерции. Затем, учитывая, что для круг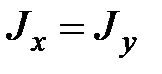а , а 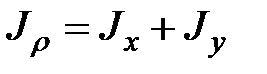, найдем .

Разобьем круг на бесконечно малые кольца толщиной d и радиусом ; площадь такого кольца 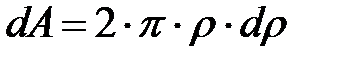. Подставляя выражение для площади кольца в выражение для 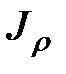и интегрируя, получим: 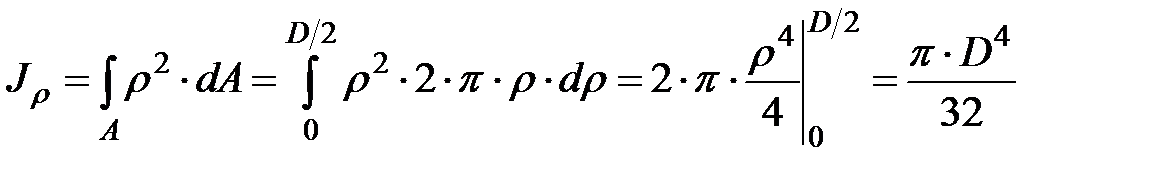Тогда .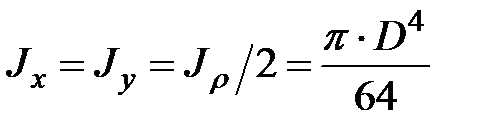

Преобразование геометрических характеристик.

Преобразование характеристик при параллельном переносе осей. Преобразование центробежного и осевых моментов инерции при вращении центральных осей. Главные центральные оси. Главные осевые моменты инерции сечения.