Математические модели микроуровня

Модели микроуровня используют дифференциальные уравнения в частных производных. Пример – уравнение нестационарной теплопроводности:

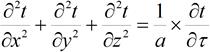
Их точное решение возможно только в редких случаях, при простых граничных условиях (граничные условия – значения искомой функции на границах тела). Поэтому точное решение для объекта в целом заменяют приближенным для его дискретной модели. Деталь (ее геометрическая форма) представляется в виде набора конечного числа элементарных объемов (элементов). Все элементы имеют простую форму. Совокупность граней элементов образует сетку. Сетка является дискретной моделью области определения искомой функции (например, механических напряжений или температуры).

Такой подход к решению задачи называется методом сеток. Применение метода сеток позволяет свести дифференциальную краевую задачу к системе алгебраических уравнений. Алгоритм метода сеток состоит из следующих основных этапов:

- построение сетки в заданной области – дискретизация задачи;

- получение системы алгебраических уравнений относительно узловых значений – алгебраизация задачи;

- решение полученной системы алгебраических уравнений.

Существует три основных способа использования метода сеток:

- метод конечных разностей;

- метод конечных элементов;

- методов граничных элементов.

Метод конечных разностей

Метод конечных разностей – самый старый метод решения краевых задач. Производная функции заменяется отношением разности ее значений при малом изменении аргумента к изменению аргумента. Например, для функции y(x) на отрезке (одномерная задача), пользуясь разложением по формуле Тейлора, можно записать:

,

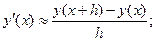
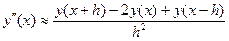где h – малое изменение аргумента, в данном случае x. Проще всего понять суть метода на примере. Пусть требуется найти решение уравнения (значение функции j при заданном X):

,

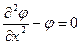удовлетворяющего следующим граничным условиям (ГУ) или значениям на границах исследуемой области (0 £ X £ 1):

j_(х=0) = 0;

j_(x=1) = 1.

Разбиваем область определения от 0 до 1 на 3 элемента. Иными словами, шаг сетки h равен h=1/3.

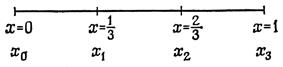
Заменяя вторую производную в дифференциальном уравнении ее аппроксимацией по формуле Тейлора, для i-го узла получаем:

¯

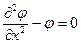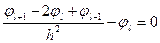или, после приведения подобных

.

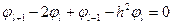Используя это уравнение, для узлов i=1 и i=2 можно записать систему линейных алгебраических уравнений:

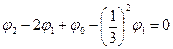(i=1)

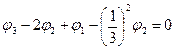(i=2)

Подставляя значения граничных условий: j₀=0 и j₃=1, получаем итоговую систему алгебраических уравнений:

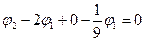	à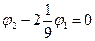
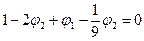	à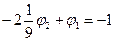

Ее решение: j₁=0.2893 и j₂=0.6107. Точное решение: j₁=0.2889 и j₂=0.6102.

Аналогичным образом можно решать задачи и в 2-, 3-мерных областях. Например, для двухмерной задачи отдельно аппроксимируются производные по X и Y. Для этого используются следующие «шаблоны»:

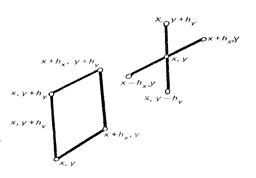
К преимуществам метода конечных разностей можно отнести возможность относительно просто (для профессионала) решать сколь угодно сложные задачи. К недостаткам – сложность задания неравномерной сетки в исследуемой области и проблемы задания ГУ на границах, непараллельных осям координат.

Метод граничных элементов

Основан на замене исходного дифференциального уравнения системой интегральных уравнений. Искомое решение ищется как сумма решений задачи для множества фиктивных источников, мощность которых подобрана так, что их суммарное воздействие обеспечивает заданные граничные условия. В простейшем случае границу объекта заменяют многоугольником, на каждой стороне которого действует фиктивный источник неизвестной мощности.

Например, для 4-угольника граничные условия – температура на гранях. Подбираются фиктивные источники тепла, которые в сумме обеспечивают заданную температуру на каждой грани. Зная мощность источников, легко рассчитать температуру в любой точке внутри 4-угольника.

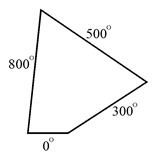
(+) Часто обеспечивает большую точность и резко уменьшает объем исходных данных, необходимых для решения. (–) МГЭ используется только для линейных задач. Он сложнее в реализации чем, например, метод конечных элементов.

Метод конечных элементов

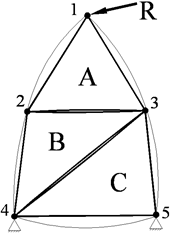
Рассмотрим использование метода конечных элементов на примере прочностного расчета пластины (рисунок 1, а). Пластина (показана тонкими линиями) нагружена силой R и жестко закреплена за основание. Аппроксимируем пластину тремя треугольными конечными элементами (КЭ) – A, B, C. Каждый КЭ соединяется с соседним только в своих вершинах – узлах. Для того чтобы это подчеркнуть, на рисунке *1 стороны некоторых треугольников искусственно отнесены друг от друга. Некоторые узлы принадлежат только одному КЭ (узлы 1 и 5), некоторые – сразу нескольким КЭ. Например, узел 2 принадлежит сразу и элементу А и элементу В; узел 3 принадлежит всем трем элементам, узел 4 – элементам В и С.

а)	б)

Рисунок 1 – Пример разбиения пластины на конечные элементы

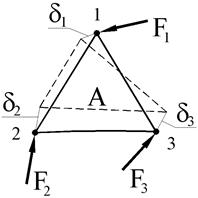
Предварительно рассмотрим какой-нибудь отдельный конечный элемент, например, А (рисунок 1, б). Со стороны остальных элементов и, в общем случае, со стороны внешней среды, на него действуют силы F₁, F₂, F₃. Под действием этих сил треугольник деформируется (показано штриховыми линиями). В результате деформации вершины треугольника переместятся на малые величины, соответственно, d₁, d₂, d₃.

Очевидно, существует связь между величинами сил и соответствующих им перемещений вершин элемента. Традиционно эта связь записывается в матричном виде:

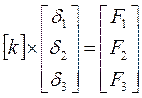(1)

где k – т.н. матрица жесткости конечного элемента. Порядок ее получения для упругой треугольной пластины подробно рассматривается ниже. Пока же отметим, что компоненты матрицы жесткости зависят от координат вершин треугольника, толщины пластины и механических свойств материала (модуля упругости E и коэффициента Пуассона m).

Далее уравнения вида (1) для всех конечных элементов объединяют в общие матрицы – отдельно матрицу сил и отдельно в глобальную матрицу жесткости. Для этого достаточно сложить все элементы матриц конечных элементов, относящихся к одному узлу. Такой процесс называется ассемблированием.

При составлении матрицы сил силы, приложенные в одном и том же узле, но действующие от разных элементов, обозначим по имени элемента с индексом узла. Например, сила, с которой элемент В действует на 2-ой узел, равна В₂, а сила, с которой элемент А действует на тот же узел, равна А₂ и т.д. Заметим, что силы, с которыми элементы действуют друг на друга, по третьему закону Ньютона равны по величине, но противоположны по направлению. Например, можно записать: A₂ + B₂ = 0, A₃+B₃+C₃=0, B₄+C₄=0. Поэтому при формировании глобальной матрицы сил существует следующее правило: если узлы (в примере 2 и 3) свободны от воздействия внешних сил и закреплений, то соответствующие этим узлам элементы глобальной матрицы сил равны нулю.

В итоге система уравнений (в матричном виде), описывающая равновесие тела под действием заданных сил и закреплений, имеет вид:

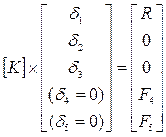(3)

где К – глобальная матрица жесткости, полученная объединением локальных матриц жесткости каждого отдельного конечного элемента; R – внешняя сила, действующая на тело; F₄, F₅ – силы, действующие в закреплениях.

Запрет на перемещения в узлах 4 и 5 формально можно записать, как d₄=0 и d₅=0. Таким образом, в итоговой системе пяти уравнений (3) остается пять неизвестных, что позволяет найти ее решение – значения перемещений d_i в каждом узле. Зная перемещения вершин (узлов), по формуле (1) рассчитываются силы, действующие на каждый элемент. По значениям действующих сил нетрудно рассчитать вызванные ими напряжения в каждом элементе.