Некоторые методы распознавания графических образов

Для оптического распознавания образов можно применить метод перебора вида объекта под различными углами, масштабами, смещениями и т. д. Для букв нужно перебирать шрифт, свойства шрифта и т. д.

Второй подход — найти контур объекта и исследовать его свойства (связность, наличие углов и т. д.)

Ещё один подход — использовать искусственные нейронные сети. Этот метод требует либо большого количества примеров задачи распознавания (с правильными ответами), либо специальной структуры нейронной сети, учитывающей специфику данной задачи.

(Статья https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D1%80%D0%B0%D1%81%D0%BF%D0%BE%D0%B7%D0%BD%D0%B0%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F_%D0%BE%D0%B1%D1%80%D0%B0%D0%B7%D0%BE%D0%B2)

Задача классификации

Классификация является наиболее простой и одновременно наиболее часто решаемой задачей Data Mining. Ввиду распространенности задач классификации необходимо четкое понимания сути этого понятия.

Приведем несколько определений.

Классификация - системное распределение изучаемых предметов, явлений, процессов по родам, видам, типам, по каким-либо существенным признакам для удобства их исследования; группировка исходных понятий и расположение их в определенном порядке, отражающем степень этого сходства.

Классификация - упорядоченное по некоторому принципу множество объектов, которые имеют сходные классификационные признаки (одно или несколько свойств), выбранных для определения сходства или различия между этими объектами.

Классификация требует соблюдения следующих правил:

• в каждом акте деления необходимо применять только одно основание;
• деление должно быть соразмерным, т.е. общий объем видовых понятий должен равняться объему делимого родового понятия;
• члены деления должны взаимно исключать друг друга, их объемы не должны перекрещиваться;
• деление должно быть последовательным.

Различают:

• вспомогательную (искусственную) классификацию, которая производится по внешнему признаку и служит для придания множеству предметов (процессов, явлений) нужного порядка;
• естественную классификацию, которая производится по существенным признакам, характеризующим внутреннюю общность предметов и явлений. Она является результатом и важным средством научного исследования, т.к. предполагает и закрепляет результаты изучения закономерностей классифицируемых объектов.

В зависимости от выбранных признаков, их сочетания и процедуры деления понятий классификация может быть:

• простой - деление родового понятия только по признаку и только один раз до раскрытия всех видов. Примером такой классификации является дихотомия, при которой членами деления бывают только два понятия, каждое из которых является противоречащим другому (т.е. соблюдается принцип: "А и не А");
• сложной - применяется для деления одного понятия по разным основаниям и синтеза таких простых делений в единое целое. Примером такой классификации является периодическая система химических элементов.

Под классификацией будем понимать отнесение объектов (наблюдений, событий) к одному из заранее известных классов.

Классификация - это закономерность, позволяющая делать вывод относительно определения характеристик конкретной группы. Таким образом, для проведения классификации должны присутствовать признаки, характеризующие группу, к которой принадлежит то или иное событие или объект (обычно при этом на основании анализа уже классифицированных событий формулируются некие правила).

Классификация относится к стратегии обучения с учителем (supervised learning), которое также именуют контролируемым или управляемым обучением.

Задачей классификации часто называют предсказание категориальной зависимой переменной (т.е. зависимой переменной, являющейся категорией) на основе выборки непрерывных и/или категориальных переменных.

Например, можно предсказать, кто из клиентов фирмы является потенциальным покупателем определенного товара, а кто - нет, кто воспользуется услугой фирмы, а кто - нет, и т.д. Этот тип задач относится к задачам бинарной классификации, в них зависимая переменная может принимать только два значения (например, да или нет, 0 или 1).

Другой вариант классификации возникает, если зависимая переменная может принимать значения из некоторого множества предопределенных классов. Например, когда необходимо предсказать, какую марку автомобиля захочет купить клиент. В этих случаях рассматривается множество классов для зависимой переменной.

Классификация может быть одномерной (по одному признаку) и многомерной (по двум и более признакам).

Многомерная классификация была разработана биологами при решении проблем дискриминации для классифицирования организмов. Одной из первых работ, посвященных этому направлению, считают работу Р. Фишера (1930 г.), в которой организмы разделялись на подвиды в зависимости от результатов измерений их физических параметров. Биология была и остается наиболее востребованной и удобной средой для разработки многомерных методов классификации.

Процесс классификации

Цель процесса классификации состоит в том, чтобы построить модель, которая использует прогнозирующие атрибуты в качестве входных параметров и получает значение зависимого атрибута. Процесс классификации заключается в разбиении множества объектов на классы по определенному критерию.

Задача кластеризации

Только что мы изучили задачу классификации, относящуюся к стратегии "обучение с учителем".

В этой части лекции мы введем понятия кластеризации, кластера, кратко рассмотрим классы методов, с помощью которых решается задача кластеризации, некоторые моменты процесса кластеризации, а также разберем примеры применения кластерного анализа.

Задача кластеризации сходна с задачей классификации, является ее логическим продолжением, но ее отличие в том, что классы изучаемого набора данных заранее не предопределены.

Синонимами термина " кластеризация " являются "автоматическая классификация ", "обучение без учителя" и "таксономия".

Кластеризация предназначена для разбиения совокупности объектов на однородные группы ( кластеры или классы). Если данные выборки представить как точки в признаковом пространстве, то задача кластеризации сводится к определению "сгущений точек".

Цель кластеризации - поиск существующих структур.

Кластеризация является описательной процедурой, она не делает никаких статистических выводов, но дает возможность провести разведочный анализ и изучить "структуру данных".

Само понятие " кластер " определено неоднозначно: в каждом исследовании свои " кластеры ". Переводится понятие кластер (cluster) как "скопление", "гроздь".

Кластер можно охарактеризовать как группу объектов, имеющих общие свойства.

Характеристиками кластера можно назвать два признака:

• внутренняя однородность;
• внешняя изолированность.

Вопрос, задаваемый аналитиками при решении многих задач, состоит в том, как организовать данные в наглядные структуры, т.е. развернуть таксономии.

Наибольшее применение кластеризация первоначально получила в таких науках как биология, антропология, психология. Для решения экономических задач кластеризация длительное время мало использовалась из-за специфики экономических данных и явлений.

В таблице 5.2 приведено сравнение некоторых параметров задач классификации и кластеризации.

Таблица 5.2. Сравнение классификации и кластерзации
Характеристика	Классификация	Кластеризация
Контролируемость обучения	Контролируемое обучение	Неконтролируемое обучение
Стратегия	Обучение с учителем	Обучение без учителя
Наличие метки класса	Обучающее множество сопровождается меткой, указывающей класс, к которому относится наблюдение	Метки класса обучающего множества неизвестны
Основание для классификации	Новые данные классифицируются на основании обучающего множества	Дано множество данных с целью установления существования классов или кластеров данных

На рис. 5.7 схематически представлены задачи классификации и кластеризации.

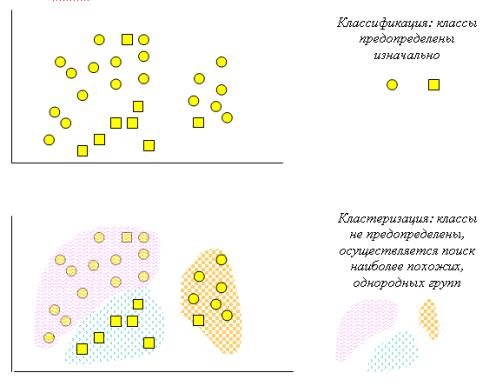
Рис. 5.7.Сравнение задач классификации и кластеризации

6 Способы определения классов объектов: перечисление, задание общих свойств. Примеры.

Разбиение рассматриваемого множества объектов на классы Ω_i может быть задано следующими способами:

1. Перечисление.Каждый класс задаётся путём прямого указания его членов.Такойподход используется в том случае, если доступна полная априорная информация о всех возможных объектах распознавания. Предъявляемые системе образы сравниваются с заданными описаниями представителей классов и относятся к тому классу, которому принадлежат наиболее сходные с ними образцы. Такой подход называют методом сравнения

с эталоном.Его недостатком является слабая устойчивость к шумам и искажениям враспознаваемых образах.

Пример.Распознавание машинопечатного шрифта.Все символы имеют чёткозаданное шрифтом начертание. Следовательно, необходимо обучить систему путём прямого указания изображений всех распознаваемых символов (т.е. путём задания эталонов):

АБ В ..... а б в ... 1 2 3 ....

Необходимо отметить, что если предполагается распознавание курсивного, полужирного или иного начертания символов шрифта, то при таком подходе будет необходимо представить каждый вариант начертания каждого символа. Это связано с характером процесса распознавания : каждый распознаваемый объект попиксельно сравнивается поочерёдно со всеми известными системе эталонами. Кроме того, способность распознавания линейных трансформаций данных эталонов требует определённых усилий на этапе предобработки.

2. Задание общих свойств.Класс задаётся указанием некоторых признаков,присущихвсем его членам. Распознаваемый объект в таком случае не сравнивается напрямую с группой эталонных объектов. В его первичном описании выделяются значения определённого набора признаков, которые затем сравниваются с заданными признаками классов. При этом для каждого признака может задаваться требование либо к его наличию/отсутствию, либо к нахождению его числового значения в установленных пределах. Такой подход называется сопоставлением по признакам . Он экономичнее метода сравнения с эталоном в вопросе количества памяти, необходимой для хранения описаний классов. Кроме того, он допускает некоторую вариативность распознаваемых образов. Однако, главной сложностью является определение полного набора признаков, точно отличающих членов одного класса от членов всех остальных.

Пример.Распознавание цифр почтовых индексов[17].Рассматривается следующий наборраспознаваемых символов (рис. 2):

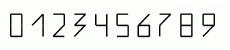
Рисунок 2: Цифры почтовых индексов

Каждый из показанных символов представляет класс распознаваемых объектов — одну из цифр. Все эти изображения построены по одному принципу — с помощью комбинирования вертикальных, горизонтальных и диагональных сегментов в определённых позициях знакомест. Для описания классов предлагаются следующие признаки:

x₁ —количество вертикальных линий минимального размера; x₂ —количество горизонтальных линий; x₃ —количество наклонных линий;

x₄ —количество горизонтальных линий снизу объекта.

С помощью этих признаков можно следующим образом задать классы цифр:

	x1	x2	x3	x4

Заметим, что набор выбранных признаков не является единственно возможным. Качество распознавания во многом зависит от того, насколько удачно разработчиком системы выбран набор признаков [8].

Дополнение к вопросу:

Перечисление

– Каждый класс задаётся путём прямого указания его членов;

– Используется, если доступна полная априорная информация о всех возможных объектах распознавания;

– Предъявляемые системе образы сравниваются с заданными описаниями представителей классов и относятся к тому классу, которому принадлежат наиболее сходные с ними образцы – метод сравнения с эталоном;

– Применим, к примеру, при распознавании машинопечатных символов определённого шрифта;

– Недостаток – слабая устойчивость к шумам и искажениям в распознаваемых образах.

Задание общих свойств:

– Класс задаётся указанием некоторых признаков, присущих всем его членам;

– В его первичном описании распознаваемого объекта выделяются значения определённого набора признаков, которые затем сравниваются с заданными признаками классов - сопоставление по признакам.

– Такой метод экономичнее метода сравнения с эталоном в вопросе количества памяти, необходимой для хранения описаний классов.

– Допускает некоторую вариативность распознаваемых образов.

– Недостаток – сложность определения полного набора признаков, точно отличающих членов одного класса от членов всех остальных.

7. Непараметрические методы распознавания образов. Алгоритм распознавания по образцу. Проблема выбора метрики.

Распознавание образов (объектов, сигналов, ситуаций, явлений или процессов) - задача идентификации объекта или определения каких-либо его свойств по его изображению (оптическое распознавание) или аудиозаписи (акустическое распознавание) и другим характеристикам.

Одним из базовых является не имеющее конкретной формулировки понятие множества. В компьютере множество представляется набором неповторяющихся однотипных элементов. Слово "неповторяющихся" означает, что какой-то элемент в множестве либо есть, либо его там нет. Универсальное множество включает все возможные для решаемой задачи элементы, пустое не содержит ни одного.

Образ - классификационная группировка в системе классификации, объединяющая (выделяющая) определенную группу объектов по некоторому признаку. Образы обладают характерным свойством, проявляющимся в том, что ознакомление с конечным числом явлений из одного и того же множества дает возможность узнавать сколь угодно большое число его представителей. Образы обладают характерными объективными свойствами в том смысле, что разные люди, обучающиеся на различном материале наблюдений, большей частью одинаково и независимо друг от друга классифицируют одни и те же объекты. В классической постановке задачи распознавания универсальное множество разбивается на части-образы. Каждое отображение какого-либо объекта на воспринимающие органы распознающей системы, независимо от его положения относительно этих органов, принято называть изображением объекта, а множества таких изображений, объединенные какими-либо общими свойствами, представляют собой образы (более подробно можно ознакомиться на сайте http://www.codenet.ru).

Методика отнесения элемента к какому-либо образу называется решающим правилом. Еще одно важное понятие - метрика, способ определения расстояния между элементами универсального множества. Чем меньше это расстояние, тем более похожими являются объекты (символы, звуки и др.) - то, что мы распознаем. Обычно элементы задаются в виде набора чисел, а метрика - в виде функции. От выбора представления образов и реализации метрики зависит эффективность программы, один алгоритм распознавания с разными метриками будет ошибаться с разной частотой.

Обучением обычно называют процесс выработки в некоторой системе той или иной реакции на группы внешних идентичных сигналов путем многократного воздействия на систему внешней корректировки. Такую внешнюю корректировку в обучении принято называть "поощрениями" и "наказаниями". Механизм генерации этой корректировки практически полностью определяет алгоритм обучения. Самообучение отличается от обучения тем, что здесь дополнительная информация о верности реакции системе не сообщается.

Адаптация - это процесс изменения параметров и структуры системы, а возможно - и управляющих воздействий, на основе текущей информации с целью достижения определенного состояния системы при начальной неопределенности и изменяющихся условиях работы.

Обучение - это процесс, в результате которого система постепенно приобретает способность отвечать нужными реакциями на определенные совокупности внешних воздействий, а адаптация - это подстройка параметров и структуры системы с целью достижения требуемого качества управления в условиях непрерывных изменений внешних условий.

Примеры задач распознавания образов:
- Распознавание букв;
- Распознавание штрих-кодов;
- Распознавание автомобильных номеров;
- Распознавание лиц и других биометрических данных;
- Распознавание речи.

8. Статистический подход в задаче распознавания образов. Использование правила Байеса.