Стационарные режимы САУ. Передаточные функции статических и астатических систем

Режим, в котором находится САУ после завершения переходного процесса, вызванного внешними воздействиями или изменением параметров системы, называется стационарным (установившимся). Различают два вида стационарного режима САУ: статический и динамический.

Стационарный статический режим (статика) – это режим, при котором система находится в состоянии покоя. Если же система находится в установившемся вынужденном движении, обусловленном соответствующим внешним воздействием, то такой ее стационарный режим называется динамическим.

Как уже отмечалось, САУ подразделяются на статические и астатические. Установим, какими особенностями должны обладать передаточные функции таких систем.

Передаточная функция замкнутой системы с единичной отрицательной обратной связью (рис. 5.1) равна:

,

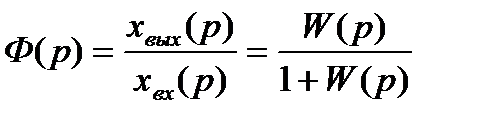где 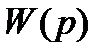– передаточная функция разомкнутой системы.

_

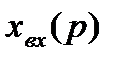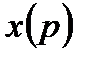Рис. 5.1. Структура САУ

Сигнал 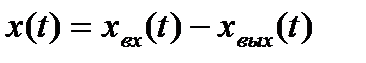– ошибка регулирования.

Передаточная функция такой системы по ошибке:

.

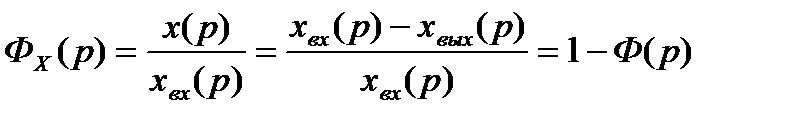
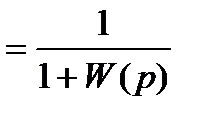Установившееся значение ошибки регулирования, определенное по теореме о конечном значении, равно:

.

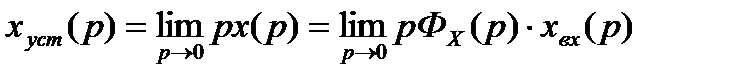Если на вход системы подан единичный ступенчатый сигнал x_вх(t) = 1(t), изображение по Лапласу которого:

,

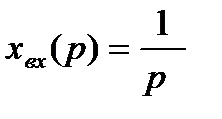то

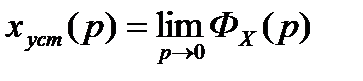. (5.1.)

Из выражения (5.1.) следует, что статическая ошиб­ка равна нулю, если передаточная функция по ошибке со­держит в числителе сомножитель p^υ, в про­тивном случае статическая ошибка не равна нулю. Указанное требования к нулям передаточной функции по ошибке 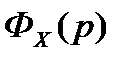равносильно тому, что передаточная функция разомкнутой системы 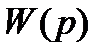должна иметь нулевой полюс кратности υ. Величина υ определяет порядок астатизма системы.

Рассмотрим статическую систему, передаточную функцию которой в разомкнутом состоянии запишем в виде:

,

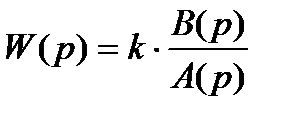где ; .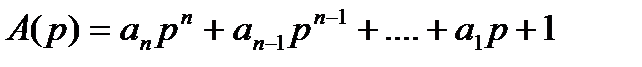

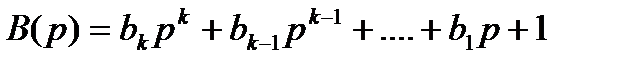Тогда передаточная функция по ошибке:

.

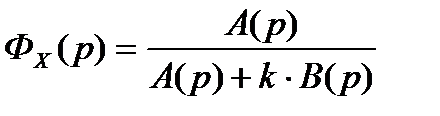В случае единичного ступенчатого входного сигнала величина установившейся ошибки (такая ошибка называется ошибкой по положению), в соответствии с выражением (5.1) будет равна:

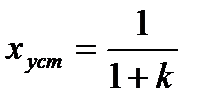. (5.2)

Передаточная функция разомкнутой системы с астатизмом первого порядка:

.

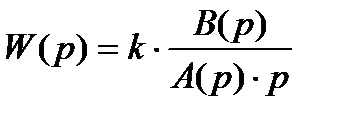Передаточная функция по ошибке для такой системы будет иметь вид:

.

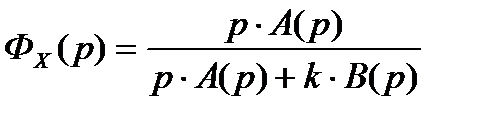Если при этом на вход системы подается единичный ступенчатый сигнал, то, в соответствии с выражением (5.1), ошибка по положению будет равна нулю (рис. 5.2, а).

Пусть на вход этой же системы подается линейно-нарастающий сигнал x_вх(t) = at, изображение по Лапласу которого:

.

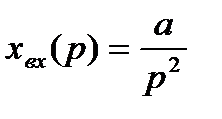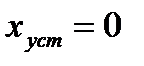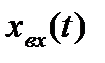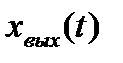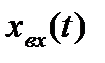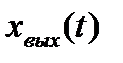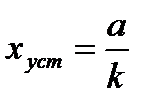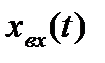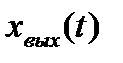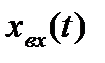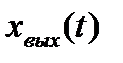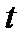а)

б)

Рис. 5.2. Реакции систем с астатизмом первого порядка на входной сигнал: а - ступенчатый; б - линейно-нарастающий

Тогда величина установившейся ошибки (такая ошибка называется ошибкой по скорости), будет равна (рис. 5.2, б):

.

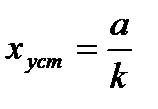Нетрудно показать, что установившаяся ошибка астатической системы с астатизмом второго порядка на линейно-нарастающий входной сигнал будет равна нулю.

Из изложенного следует, что для повышения точности САУ необходимо увеличивать коэффициент усиления системы и повышать порядок ее астатизма. Очевидно, что и тот, и другой подход сопряжен с понижением запаса устойчивости системы.

Коэффициенты ошибки системы

Разложим передаточную функцию по ошибке в ряд по возрастающим степеням p:

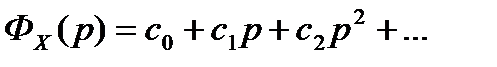
Тогда 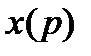– изображение ошибки может быть записано в виде:

,

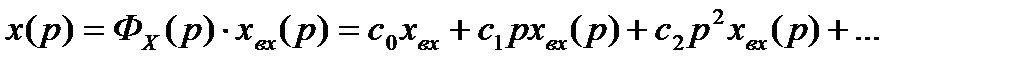следовательно,

.

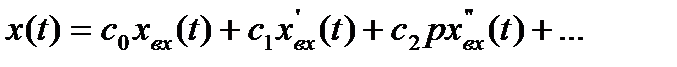Коэффициенты 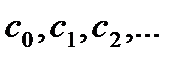называются коэффициентами ошибки: 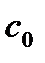- коэффициент ошибки по положению; 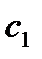- коэффициент ошибки по скорости; 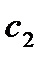- коэффициент ошибки по ускорению.

Если с достаточной точностью входной сигнал 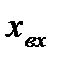(t) можно представить в виде:

,

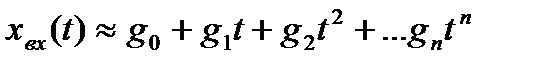то в разложении передаточной функции 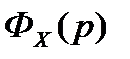следует ограничиться конечным числом членов.

Значения коэффициентов ошибки можно вычислить различными способами, например, используя следующие выражения:

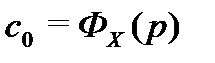| _{p = 0;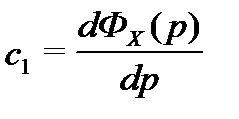} | _{p = 0;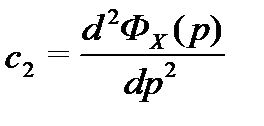} | _{p = 0} и т.д.

В статической системе 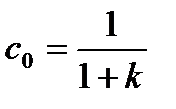; в астатической системе с астатизмом первого порядка 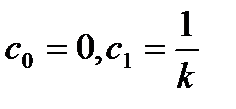; в астатической системе с астатизмом второго порядка .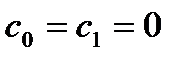