Построение модели каустики для плоскости, заданной в параметрическом виде.
Построение каустик в пространстве производиться подобно двумерному случаю.
Алгоритм
1. Строим геометрические фигуры, с определенными ограничениями.
2. Задаем плоскость, которая будет выступать в роли источника света.
3. Задаем точку на плоскости, из которой будет исходить луч света
4. Задаем направление вектора при помощи второй точки.
5. Через начальную точку, и направление вектора находим точку пересечения луча с плоскостью.
6. Строим отрезок соединяющий точку на прямой и точку пересечения.
7. Находим нормаль.
8. Строим направление отраженного от плоскости луча.
9. Строим прямую, определяющую направление отраженного луча.
3.3.Написание программных процедур СКМ Maple
Двумерный случай
Для начала задаем параметрическое уравнение кривой второго порядка:
r:=[t^2/(2*3),t]:
Далее вводим координаты начальной точки:
x[0]:=10;
y[0]:=5;
Задаем направляющий вектор:
x_dir[0]:=-1;
y_dir[0]:=.3;
Выводим уравнение прямой , с учетом того вектор направления может быть равен нулю:
if x_dir[0]=0 then
a:=[x[0],y_dir[0]*k+y[0]];
else
a:=[x_dir[0]*k+x[0],y_dir[0]*k+y[0]]:
end if:
Описываем уравнение наше кривой и ограничения на которых она будет строиться:
plt[01]:=plot([op(r),t=-20..20],scaling=constrained):
Описываем точку,при помощи которой будем задавать направление
луча:
plt[02]:=point([x[0],y[0]]):
Описываем точку, которая будет задавать направления луча света
выводим все значения, которые мы записали:
plt[03]:=point([x[0]+x_dir[0],y[0]+y_dir[0]]):
Описываем уравнение нашей прямой и ограничения на которых она будет задаваться:
plt[04]:=plot([op(a),k=-20..20],scaling=constrained):
Выводим все значения, которые мы получили (Рис.3.4):
display([plt[01],plt[02],plt[03],plt[04]],scaling=constrained,axes=none);

Рисунок 3.4-Построение кривой, начальной точки, и вектора направления
Следующим шагом записываем систему уравнений, для нахождения точки падения луча:
tmp1:=solve(eq,{t,k});
Находим точки пересечения прямой и кривой:
y[1]:=rhs(tmp1[1][2]):
x[1]:=subs(t=rhs(tmp1[1][2]),r[1]):
y[2]:=rhs(tmp1[2][2]):
x[2]:=subs(t=rhs(tmp1[2][2]),r[1]):
Рассчитываем расстояние между корнями получившихся уравнений и начальной точкой:
per1:=sqrt((x[1]-x[0])^2+(y[1]-y[0])^2):
per2:=sqrt((x[2]-x[0])^2+(y[2]-y[0])^2):
Выбираем подходящую нам точку при помощи задания условия:
if evalf(sqrt((x[1]-x[0])^2+(y[1]-y[0])^2))<(sqrt((x[2]-x[0])^2+(y[2]-y[0])^2)) then
x[11]:=x[1]
else x[11]:=x[2]
end if;
if evalf(sqrt((x[1]-x[0])^2+(y[1]-y[0])^2))<(sqrt((x[2]-x[0])^2+(y[2]-y[0])^2)) then
y[11]:=y[1]
else y[11]:=y[2]
end if;
Для вычисления касательной находим производную:
dr:=diff(r,t);
Находим касательную:
kas:=evalf(subs(t=y[11],dr));
Задаем условие для вывода нормали и выводим нормаль:
norm1:=[kas[2],-kas[1]];
if norm1[1]*(x[0]-x[11])+norm1[2]*(y[0]-y[11])<0
then norm1:=[-kas[2],kas[1]];
end if;
Описываем точку определяющую вектор нормали:
plt[07]:=point([x[11]+norm1[1],y[11]+norm1[2]]):
Выводим все значения, которые мы получили (Рис.3.5):
display([plt[01],plt[02],plt[04],plt[07]],scaling=constrained,axes=none);

Рисунок 3.5-Построение кривой, начальной точки, точки пересечения и направления нормали
По ранее выведенным формулам находим поэтапно вектор отражения.
Первым этапом находим отношение скалярного произведения вектора направления и вектору нормали к скалярному произведению вектора нормали самого на себя:
n1:=(x_dir[0]*norm1[1]+y_dir[0]*norm1[2])/(norm1[1]*norm1[1]+norm1[2]*norm1[2]):
Затем находим удвоенное произведение вектора нормали на получившуюся константу n1:
n2:=[norm1[1]*2*n1,norm1[2]*2*n1]:
Вычитаем из вектора направления вектор n2:
l:=[x_dir[0]-n2[1],y_dir[0]-n2[2]]:
Получившийся вектор l и будет вектором отражения. Запишем уравнение отражённой прямой:
lk:=solve((x-x[11])/l[1]=(y-y[11])/l[2],y);
Описываем уравнение отраженной прямой:
plt[08]:=plot(lk,x=x[11]-5..x[11],scaling=constrained):
Выводим все значения которые мы получили (Рис.3.6):
display([plt[01],plt[02],plt[04],plt[05],plt[08]],scaling=constrained,axes=none);

Рисунок 3.6-Построение кривой, начальной точки, и вектора направления
Далее пишем процедуру для некоторого количества лучей.
Для начала зададим входные параметры : кривую в параметрическом виде и ограничения для нее:
r1:=[t^2/(2*60),t]:
t1:=-10:
t2:=10:
1)Затем перейдем к первой процедуре. Первая процедура будет заполнять заданный нами массив определенными значениями. В данной процедуре будут заполняться только две точки, первая из которых является начальной, а вторая характеризует вектор направления:
prbRefLines:=proc(L,h,d1,d2,N)
global Line_, r1;
local dh,dir,i;
dir:=[d1,d2]:
dh:=(h/N):
for i from 1 to N do
Line_[i]:=[[L,-h/2+(i-1)*dh],dir,[0,0],[0,0]];
end do:
end proc:
2)Вторая процедура будет считать точку пересечения и точку характеризующую вектор направления луча отражения:
prbRefArray:=proc(L,N)
global Line_, r1:
local dir_,x,y,a_,tmp1,kas,per1,per2,norm,l,n1,n2,k,i,dr;
# вектор направления
for i from 1 to N do
# расчет пересечения:
a_:=[k*Line_[i][2][1]+Line_[i][1][1],k*Line_[i][2][2]+Line_[i][1][2]]:
if Line_[i][2][1]=0 then
a_:=x=Line_[i][1][1]:
else
a_:=[k*Line_[i][2][1]+Line_[i][1][1],k*Line_[i][2][2]+Line_[i][1][2]]:
end if:
solve({r1[1]=a_[1],r1[2]=a_[2]},{t,k}):
tmp1:=solve({r1[1]=a_[1],r1[2]=a_[2]},{t,k}):
y[1]:=rhs(tmp1[1][2]):
x[1]:=subs(t=rhs(tmp1[1][2]),r1[1]):
y[2]:=rhs(tmp1[2][2]):
x[2]:=subs(t=rhs(tmp1[2][2]),r1[1]):
per1:=evalf(sqrt((x[1]-Line_[i][1][1])^2+(y[1]-Line_[i][1][2])^2)):
per2:=evalf(sqrt((x[2]-Line_[i][1][1])^2+(y[2]-Line_[i][1][2])^2)):
if evalf(sqrt((x[1]-Line_[i][1][1])^2+(y[1]-Line_[i][1][2])^2))<evalf(sqrt((x[2]-Line_[i][1][1])^2+(y[2]-Line_[i][1][2])^2)) then
Line_[i][3][1]:=x[1]
else Line_[i][3][1]:=x[2]
end if:
if evalf(sqrt((x[1]-Line_[i][1][1])^2+(y[1]-Line_[i][1][2])^2))<evalf(sqrt((x[2]-Line_[i][1][1])^2+(y[2]-Line_[i][1][2])^2)) then
Line_[i][3][2]:=y[1]
else Line_[i][3][2]:=y[2]
end if:
# Нормаль в новой точке
dr:=diff(r1,t):
kas:=evalf(subs(t=Line_[i][3][2],dr)):
norm:=[kas[2],-kas[1]]:
if evalf(norm[1]*(Line_[i][1][1]-Line_[i][2][1])+norm[2]*(Line_[i][1][2]-Line_[i][2][2]))<0 then norm:=[-kas[2],kas[1]]:
end if:
#Вектор направления отражения
n1:=(Line_[i][2][1]*norm[1]+Line_[i][2][2]*norm[2])/(norm[1]*norm[1]+norm[2]*norm[2]):
n2:=[norm[1]*2*n1,norm[2]*2*n1]:
l:=[Line_[i][2][1]-n2[1],Line_[i][2][2]-n2[2]]:
#точка отраженная
Line_[i][4][1]:=l[1]:
Line_[i][4][2]:=l[2]:
end do:
end proc:
3) Третья процедура будет демонстрировать лучи падения и лучи отражения:
pprbLines:=proc(L,h,N)
global r1,t1,t2:
local pltprb,pltLines,pltLines1;
print(r1);
pltprb:=plot([op(r1),t=t1..t2],scaling=constrained,
color=black,
thickness=3):
pltLines:=display(
seq(
line(
Line_[i][1],
Line_[i][3],
color=red),
i=1..N),
insequence=false,
scaling=constrained
);
pltLines1:=display(
seq(
line(
Line_[i][3],
Line_[i][4],
color=green),
i=1..N),
insequence=false,
scaling=constrained
);
display([pltLines,pltprb,pltLines1],scaling=constrained,axes=none);
end proc:
И самая главная процедура которая будет включать три предыдущие и
выводить наши отражения:
Mainproc:=proc(L,h,d1,d2,N)
global r1,t1,t2:
prbRefLines(L,h,d1,d2,N):
prbRefArray(L,N):
pprbLines(L,h,N):
end proc:
Mainproc(20,20,-10,-.1,10);
eval(Line_):
В результате получим следующую картинку (Рис.3.7).

Рисунок 3.7-Каустика, при отражении лучей от параболы (параллельно падающие)
Аналогично записывается написание процедур для пучка света с поправками начальные условия. Процедуру будем задавать в более удобной для нас форме. Процедура будет включать в себя три под процедуры, у каждой из которых будет своя функция (рис.3.8).


Рисунок 3.8-Каустика, при отражении лучей от параболы(пучок)
Трехмерный случай
Отражение на плоскости будем рассматривать на примере параболоида.
Задаем начальные условия для прямой:
x[0]:=0:
y[0]:=0:
z[0]:=0:
ax:=1:
ay:=-.3:
az:=10:
Задаем уравнение плоскости и уравнения прямой:
a:=x^2+y^2-z;
b:=x-x[0]/ax=y-y[0]/ay;
c:=y-y[0]/ay=(z-z[0])/az;
Рисуем прямую и параболоид:
pl_b:=spacecurve([ax*t+x[0],ay*t+y[0],az*t+z[0]],t=-10..10):
pl_a:=implicitplot3d(a,x=-10..10,y=-10..10,z=-10..10,numpoints=5000):
Находим точку пересечения прямой и плоскости:
sol:=evalf(solve({a,b,c},{x,y,z}));
x_:=evalf(subs(sol,x));
y_:=evalf(subs(sol,y));
z_:=evalf(subs(sol,z));
pl_b:=spacecurve([ax*t+x[0],ay*t+y[0],az*t+z[0]],t=-1..1):
pl_a:=implicitplot3d(a,x=-10..10,y=-10..10,z=-10..10,numpoints=5000):
pl_c:=pointplot3d([x_,y_,z_],color=red);
Находим производные в точках :
x1:=subs({x=x_,y=y_,z=z_},diff(a,x)):
y1:=subs({x=x_,y=y_,z=z_},diff(a,y)):
z1:=subs({x=x_,y=y_,z=z_},diff(a,z)):
Вектор прямой задается следующим образом:
l:=[ax,ay,az];
Вектор нормали задается следующим образом:
n1:=[x1,y1,z1];4
Уравнение нормали и вывод:
pl_e:=spacecurve([x1*t+x_,y1*t+y_,z1*t+z_],t=-8..4,color=green):
Аналогично двумерному случаю находим вектор отражения при помощи вектора падения луча и вектора нормали:
k:=dotprod(l,n1)/dotprod(n1,n1);
p:=[2*k*n1[1],2*k*n1[2],2*k*n1[3]];
r:=l-p;
Вектор l будет вектором отражения.
Задаем уравнение отраженного луча, и обозначаем его:
b1:=(x-x_)/r[1]=(y-y_)/r[2];
c1:=(y-y_)/r[2]=(z-z_)/r[3];
pl_d:=spacecurve([r[1]*t+x_,r[2]*t+y_,r[3]*t+z_],t=-1..1,color=yellow):
Выводим луч падения (фиолетовый), нормаль (зеленая), отраженный луч (желтый) (Рис.3.8).
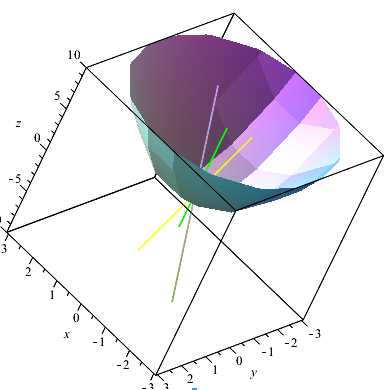
Рисунок 3.8-Отражение луча от плоскости.
Заключение
В ходе данной работы был рассмотрен теоретический материал по теме каустик и были изучены их свойства .Также в ходе магистерской диссертации была изучена среда СКМ Maple. Была создана процедура для моделирования каустик для кривых второго порядка.
Таким образом, цели, поставленные в квалификационной работе, выполнены.
Список использованной литературы
1. Burridge, R. Asymptotic evaluation of integrals related to time-domain fields near caustics, SIAM J. Appl. Math., 55:2, 1995.
2. Андреев, А.Н. Каустики на плоскости/ А.Н. Андреев, А.А. Панов «Квант» -2010. -№3.
3. Арнольд, В. И. Особенности каустик и волновых фронтов, В.И. Арнольд - М.: Фазис, 1996.
4. Арнольд, В. И. Теория катастроф / Арнольд В. И. М.: Наука, 1990.
5. Баев, А. В. Математическое моделирование волн в слоистых средах вблизи каустики/ А. В. Баев// Матем. Моделирование-2013- 25:12-С.83-102
6. Гольдин, С.В. Сейсмическое волновое поле в близи каустик: анализ во временной области/ С.В. Гольдин, А.А. Дучков //Физика Земли. - 2002.- №7. С.56–66.
7. Дьяконов, В.П. Maple 9.5/10 в математике, физике и образовании/ В.П. Дьяконов- М.: СОЛОН-Пресс, 2006. - 720 с.
8. Кирсанов, М. Н. Задачи по теоретической механике с решениями в Maple 11. М.: Физматлит, 2010, 264с.
9. Кирсанов, М.Н. Maple и Maplet. Решения задач механики / Кирсанов М.Н.-М.: Лань, 2012. -512с.
10. Лонгейр, М. Крупномасштабная структура Вселенной/ Ред. М. Лонгейр, Я. Эйнасто. - М.: Мир, 1981.
11. Постон, Т. Теория катастроф и ее применения/ Постон Т., Стюарт И. - М.: Мир, 1980.
12. Яновская, Т.Б. Численный метод расчета поля поверхностной волны при наличии каустик / Яновская Т.Б., Гейгер М.А.//Физика Земли. - 2007.
Приложение А. Программные процедуры моделирования каустик
#Отражение от произвольной кривой(параллельное падение лучей)
> restart:
with(plots):
with(plottools):
> prbRefLines:=proc(L,h,d1,d2,N)
global Line_;
local dh,dir,i;
dir:=[d1,d2]:
dh:=(h/N):
for i from 1 to N do
Line_[i]:=[[L,-h/2+(i-1)*dh],dir,[0,0],[0,0]];
end do:
end proc:
> prbRefLines(5,10,-1,-.1,50);
eval(Line_):
> prbRefArray:=proc(p,L,N)
global Line_:
local dir_,x,y,a_,r1,tmp1,kas,per1,per2,norm,l,n1,n2,k,i,dr;
#print(Line_[1]);
# вектор направления
for i from 1 to N do
#print(Line_[i][2][1]):
Line_[i][2][2]:
# расчет пересечения:
a_:=[k*Line_[i][2][1]+Line_[i][1][1],k*Line_[i][2][2]+Line_[i][1][2]]:
if Line_[i][2][1]=0 then
a_:=x=Line_[i][1][1]:
else
a_:=[k*Line_[i][2][1]+Line_[i][1][1],k*Line_[i][2][2]+Line_[i][1][2]]:
end if:
#print(a_);
r1:=[t^2/(2*p),t]:
solve({r1[1]=a_[1],r1[2]=a_[2]},{t,k}):
tmp1:=solve({r1[1]=a_[1],r1[2]=a_[2]},{t,k});
y[1]:=rhs(tmp1[1][2]):
x[1]:=subs(t=rhs(tmp1[1][2]),r1[1]):
y[2]:=rhs(tmp1[2][2]):
x[2]:=subs(t=rhs(tmp1[2][2]),r1[1]):
per1:=sqrt((x[1]-Line_[i][1][1])^2+(y[1]-Line_[i][1][2])^2):
per2:=sqrt((x[2]-Line_[i][1][1])^2+(y[2]-Line_[i][1][2])^2):
#print([per1,per2]):
if evalf(sqrt((x[1]-Line_[i][1][1])^2+(y[1]-Line_[i][1][2])^2))<evalf(sqrt((x[2]-Line_[i][1][1])^2+(y[2]-Line_[i][1][2])^2)) then
Line_[i][3][1]:=x[1]
else Line_[i][3][1]:=x[2]
end if:
if evalf(sqrt((x[1]-Line_[i][1][1])^2+(y[1]-Line_[i][1][2])^2))<evalf(sqrt((x[2]-Line_[i][1][1])^2+(y[2]-Line_[i][1][2])^2)) then
Line_[i][3][2]:=y[1]
else Line_[i][3][2]:=y[2]
end if:
# Нормаль в новой точке
dr:=diff(r1,t):
kas:=evalf(subs(t=Line_[i][3][2],dr)):
norm:=[kas[2],-kas[1]]:
if evalf(norm[1]*(Line_[i][1][1]-Line_[i][2][1])+norm[2]*(Line_[i][1][2]-Line_[i][2][2]))<0 then norm:=[-kas[2],kas[1]]:
end if;
#norm1:
#Вектор направления отражения
n1:=(Line_[i][2][1]*norm[1]+Line_[i][2][2]*norm[2])/(norm[1]*norm[1]+norm[2]*norm[2]):
n2:=[norm[1]*2*n1,norm[2]*2*n1]:
l:=[Line_[i][2][1]-n2[1],Line_[i][2][2]-n2[2]]:
#точка отраженная
Line_[i][4][1]:=l[1]:
Line_[i][4][2]:=l[2]:
end do:
end proc:
> prbRefArray(60,10,50):
> pprbLines:=proc(p,L,h,N)
local pltprb,pltLines,pltLines1,r1;
#
r1:=[t^2/(2*p),t]:
print(r1);
pltprb:=plot([op(r1),t=-10..10],scaling=constrained,
color=black,
thickness=3):
#
pltLines:=display(
seq(
line(
Line_[i][1],
Line_[i][3],
color=red),
i=1..N),
insequence=false,
scaling=constrained
);
pltLines1:=display(
seq(
line(
Line_[i][3],
Line_[i][4],
color=red),
i=1..N),
insequence=false,
scaling=constrained
);
display([pltLines,pltprb,pltLines1],scaling=constrained,axes=none);
end proc:
> pprbLines(60,200,10,10);
#Отражение от произвольной кривой(пучок лучей)
> restart:
with(plots):
with(plottools):
> r1:=[t^2/(200),t]:
t1:=-20:
t2:=20:
> prbRefLines:=proc(L,h,N)
global Line_, r1;
local dh,dir,i,dL;
dL:=L/2;
dh:=(h/N):
for i from 1 to N do
Line_[i]:=[[L,0],[L-dL-L,-h/2+(i-1)*dh],[0,0],[0,0]];
end do:
end proc:
> prbRefLines(5,10,5);
> prbRefArray:=proc(L,N)
global Line_, r1:
local dir_,x,y,a_,tmp1,kas,per1,per2,norm,l,n1,n2,k,i,dr;
# вектор направления
for i from 1 to N do
# расчет пересечения:
a_:=[k*Line_[i][2][1]+Line_[i][1][1],k*Line_[i][2][2]+Line_[i][1][2]]:
if Line_[i][2][1]=0 then
a_:=x=Line_[i][1][1]:
else
a_:=[k*Line_[i][2][1]+Line_[i][1][1],k*Line_[i][2][2]+Line_[i][1][2]]:
end if:
solve({r1[1]=a_[1],r1[2]=a_[2]},{t,k}):
tmp1:=evalf(solve({r1[1]=a_[1],r1[2]=a_[2]},{t,k})):
Line_[i][3][1]:=subs(k=rhs(tmp1[1]),a_[1]):
Line_[i][3][2]:=subs(k=rhs(tmp1[1]),a_[2]):
dr:=diff(r1,t):
kas:=evalf(subs(t=Line_[i][3][2],dr)):
norm:=[kas[2],-kas[1]]:
if evalf(norm[1]*(Line_[i][1][1]-Line_[i][2][1])+norm[2]*(Line_[i][1][2]-Line_[i][2][2]))<0 then norm:=[-kas[2],kas[1]]:
end if:
#Вектор направления отражения
n1:=(Line_[i][2][1]*norm[1]+Line_[i][2][2]*norm[2])/(norm[1]*norm[1]+norm[2]*norm[2]):
n2:=[norm[1]*2*n1,norm[2]*2*n1]:
l:=[Line_[i][2][1]-n2[1],Line_[i][2][2]-n2[2]]:
#точка отраженная
Line_[i][4][1]:=l[1]:
Line_[i][4][2]:=l[2]:
end do:
end proc:
> prbRefArray(10,5):
> pprbLines:=proc(L,h,N)
global r1,t1,t2:
local pltprb,pltLines,pltLines1;
pltprb:=plot([op(r1),t=t1..t2],scaling=constrained,
color=black,
thickness=3):
pltLines:=display(
seq(
line(
Line_[i][1],
Line_[i][3],
color=red),
i=1..N),
insequence=false,
scaling=constrained
);
pltLines1:=display(
seq(
line(
Line_[i][3],
2*Line_[i][4],
color=green),
i=1..N),
insequence=false,
scaling=constrained
);
display([pltLines,pltprb,pltLines1],scaling=constrained,axes=none);
end proc:
> pprbLines(1,20,1);
> pprbLines(200,.5,2):
> Mainproc:=proc(L,h,N)
global r1,t1,t2:
prbRefLines(L,h,N):
prbRefArray(L,N):
pprbLines(L,h,N):
end proc:
> Mainproc(100,20,10);
#Отражение от параметрически заданной плоскости
restart:
with(plots):
with(plottools):
with(linalg):
x[0]:=0:
y[0]:=0:
z[0]:=0:
ax:=1:
ay:=-.3:
az:=10:
a:=x^2+y^2-z;
b:=x-x[0]/ax=y-y[0]/ay;
c:=y-y[0]/ay=(z-z[0])/az;
diff(a,y);
pl_b:=spacecurve([ax*t+x[0],ay*t+y[0],az*t+z[0]],t=-10..10,color=black):
pl_a:=implicitplot3d(a,x=-10..10,y=-10..10,z=-10..10,numpoints=5000):
display([pl_a,pl_b]);
sol:=evalf(solve({a,b,c},{x,y,z}));
x_:=evalf(subs(sol,x));
y_:=evalf(subs(sol,y));
z_:=evalf(subs(sol,z));
pl_b:=spacecurve([ax*t+x[0],ay*t+y[0],az*t+z[0]],t=-1..1):
pl_a:=implicitplot3d(a,x=-10..10,y=-10..10,z=-10..10,numpoints=5000):
pl_c:=pointplot3d([x_,y_,z_],color=red);
display([pl_a,pl_b,pl_c]);
x1:=subs({x=x_,y=y_,z=z_},diff(a,x)):
y1:=subs({x=x_,y=y_,z=z_},diff(a,y)):
z1:=subs({x=x_,y=y_,z=z_},diff(a,z)):
l:=[ax,ay,az];
n1:=[x1,y1,z1];
pl_e:=spacecurve([x1*t+x_,y1*t+y_,z1*t+z_],t=-8..4,color=green):
n1[1];
k:=dotprod(l,n1)/dotprod(n1,n1);
p:=[2*k*n1[1],2*k*n1[2],2*k*n1[3]];
r:=l-p;
b1:=(x-x_)/r[1]=(y-y_)/r[2];
c1:=(y-y_)/r[2]=(z-z_)/r[3];
pl_d:=spacecurve([r[1]*t+x_,r[2]*t+y_,r[3]*t+z_],t=-1..1,color=yellow):
display([pl_a,pl_b,pl_d,pl_e]);
#Частные случаи изображения каустики
> restart:
with(plots):
with(plottools):
> r:=[u,u^2];
r[2];
> pl_a:=plot([op(r),u=-4..4],scaling=constrained);
> cx:=r[1]-(diff(r[2],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));
cy:=r[2]+(diff(r[1],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));
> cx:=r[1]-(diff(r[2],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));
cy:=r[2]+(diff(r[1],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));
> l:=[cx,cy];
> pl_b:=plot([op(l),u=-0.7..0.7],scaling=constrained,color=blue);
> display([pl_a,pl_b]);
> restart:
with(plots):
with(plottools):
> a:=2;
b:=3;
> r:=[a*cos(u),b*sin(u)];
r[2];
> pl_a:=plot([op(r),u=1/2*Pi..3/2*Pi],scaling=constrained);
plot([op(r),u=1/2*Pi..3/2*Pi],scaling=constrained);
> cx:=r[1]-(diff(r[2],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));
cy:=r[2]+(diff(r[1],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));
> l:=[cx,cy];
> pl_b:=plot([op(l),u=-4..4],scaling=constrained,color=blue);
> display([pl_a,pl_b]);
> restart:
with(plots):
with(plottools):
> a:=6;
b:=20;
> r:=[a*cosh(u),b*sinh(u)];
r[2];
> pl_a:=plot([op(r),u=-2*Pi..2*Pi],scaling=constrained);
plot([op(r),u=-2*Pi..2*Pi],scaling=constrained);
> cx:=r[1]-(diff(r[2],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));
cy:=r[2]+(diff(r[1],u))*((diff(r[1],u))^2+(diff(r[2],u))^2)/((diff(r[1],u))*(diff(r[2],u$2))-(diff(r[2],u))*(diff(r[1],u$2)));
> l:=[cx,cy];
> pl_b:=plot([op(l),u=-2..2],scaling=constrained,color=blue);
> display([pl_a,pl_b]);
