Построение модели каустики для кривой второго порядка, заданной в параметрическом виде.

В данной работе рассматривается два случая :

1)Когда источником света выступают точки находящиеся на заданном расстоянии друг от друга на заданной прямой

2)Когда источником света выступает пучок света.

Для каждого из этих случаев рассматриваются следующие модели, состоящие из:

1.Источника света (Пучок или параллельные лучи)

2.Отражающей поверхности (кривая) заданной в параметрическом виде.

3.Лучей света, описываемых законами геометрической оптики.

Модель источников света

Для начала рассмотрим случай, когда источником света выступает прямая на которой расположены точки, на прямой параллельной Oy (x=const) и отдалённой от вершины заданной кривой на расстоянии L.

Источники света равномерно располагаются на заданной прямой с шагом h.

Все источники на заданной прямой излучают свет в одинаковом направлении, и под определенным углом к оси абсцисс.

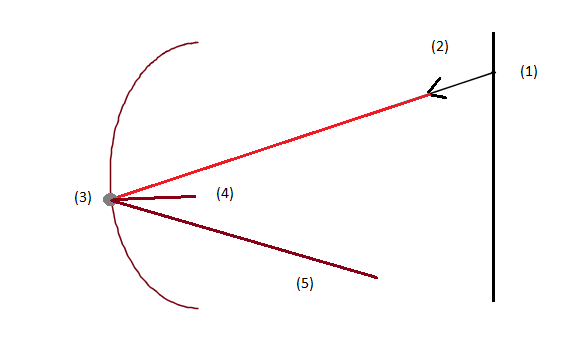
Рисунок 3.1-Построение отражения луча

В качестве источника света (рис.3.1) возьмем прямую (1), из которой будут выходить лучи света, заданные через направляющий вектор (2). В работе я буду рассматривать различные вариации направления вектора и начальных данных прямой . Исследую и рассмотрю различные прямые и различные источники света , а также различное количество лучей падающий на заданную кривую.

Геометрическая оптика

Геометрическая оптика - это раздел оптики, рассматривающий законы излучения света в различных средах и отражения света от различного вида поверхностей.

Закон отражения света

Луч света в определенной среде прямолинеен до того момента, пока он не достигнет границы данной среды с другой средой. На границе этих сред луч света изменяет свое направление. Часть света (а в ряде случаев и весь свет) возвращается в первую среду. Это явление называется отражением света. Одновременно свет частично проходит во вторую среду, меняя при этом направление своего распространения -преломляется.

Вычисление отражённого луча

Если использовать вектора, то решение находиться в более простом виде (рис.3.2):

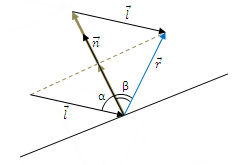
Рисунок 3.2-Геометрическое представление отражения луча

Для того чтобы найти вектор отражения нам нужно из вектора направления света вычесть удвоенное произведение вектора нормали на отношение скалярного произведения вектора направления света и нормали к скалярному произведению вектора нормали самого на себя:

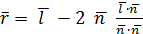(3.1)

Делит на скалярное произведение нормали самой на себя не нужно ,если данная нормаль уже нормирована.
Если прямая задана точкой ( 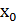, 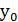) и вектором направления ( 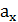, 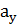), то вектор нормали (ненормированный). В некоторых случаях нужно знать знак нормали , чтобы знать, какая сторона прямой «внешняя».

Алгоритм построения для первого источника света(параллельные лучи)(Рис.3.3):

1. Построение кривой .Кривая должна быть задана в параметрическом виде.

2. Задаем прямую на которой будут располагаться источники света.

3. Задаем точку на данной прямой из которой будет исходить луч света.

4.Задаем направление вектора источника света .

5. При помощи точки и направляющего вектора вычисляем уравнение прямой.

6. Строим отрезок соединяющий точку на прямой и точку пересечения.

7. Находим нормаль.

8.Строим направление отраженной от кривой луча.
9.Строим прямую, определяющую направление отраженного луча.

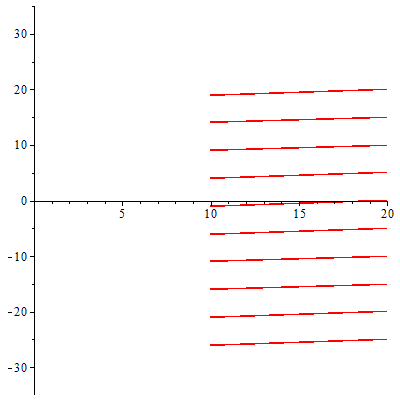
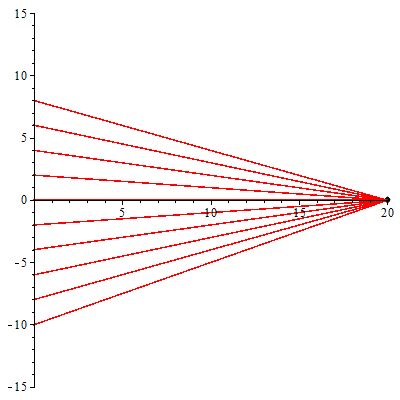
Рисунок 3.3-Параллельно направленные Рисунок 3.4-Пучок света

лучи

Алгоритм построения для второго источника света(Пучок)(Рис.3.4):

1. Построение кривой .Кривая должна быть задана в параметрическом виде.

2. Задаем точку источники света.

3. Задаем прямую на которой будут располагаться координаты направляющих векторов.

4.Задаем направление вектора источника света .

5. При помощи точки и направляющего вектора вычисляем уравнение прямой.

6. Строим отрезок соединяющий точку на прямой и точку пересечения.

7. Находим нормаль.

8.Строим направление отраженной от кривой луча
9.Строим прямую, определяющую направление отраженного луча

В данном примере будем рассматривать в качестве произвольной кривой кривую второго порядка параболу.

Ее уравнение в параметрическом виде будет выглядеть следующим образом:

,

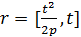(3.2)

где t-параметр.

Уравнение прямой будет выведено при помощи начальной точки и вектора направления:

,

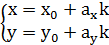(3.3)

где k-параметр , 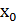- координата начальной точки на оси Ox, 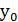-координата начальной точки на оси Oy , 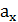-координата направления вектора на оси Ox, 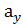-координата направления вектора на оси Oy.

Для нахождения точек пересечение запишем наше уравнение в векторном виде:

,

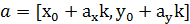(3.4)

Затем нужно найти точки пересечения, точки пересечение получим приравняв по координатам части пар метрически заданных функций:

, ,

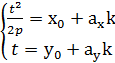(3.5)

При решении данной системы получим коэффициенты 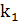, , 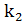, 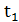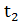. Далее нам нужно выбрать подходящие нам. Выбирать будем при помощи вычисления расстояния от точки на прямой источников света до каждой из полученных пары решений.