Амплитудно-частотная характеристика связанных контуров
Поскольку выходной величиной связанных контуров является ток вторичного контура, или пропорциональное ему напряжение, то в качестве АЧХ связанных контуров рассмотрим зависимость модуля нормированного тока вторичного контура от частоты.
С этой целью проанализируем ток вторичного контура связанных контуров с индуктивной трансформаторной связью (рис. 13.1, а), при которой сопротивление связи 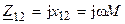 , где
, где 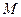 — взаимная индуктивность.
— взаимная индуктивность.
Рассмотрим наиболее простой случай, когда контура имеют одинаковые параметры элементов 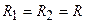 ,
, 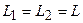 и
и 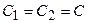 . Тогда резонансные частоты, характеристические сопротивления и добротности контуров будут также одинаковыми:
. Тогда резонансные частоты, характеристические сопротивления и добротности контуров будут также одинаковыми: 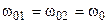 ,
, 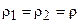 ,
, 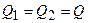 .
.
Используя выражение (14.2) проанализируем ток вторичного контура
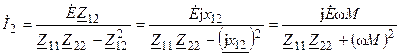 .
.
Если выразить комплексные сопротивления контуров через их сопротивления потерь и обобщённые расстройки 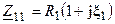 и
и 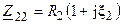 , то с учётом равенства параметров контуров получим
, то с учётом равенства параметров контуров получим 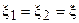 и
и 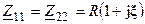 .
.
Поставляя полученное выражение в предыдущую формулу, находим
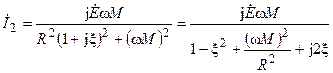 .
.
Определим максимальное значение тока вторичного контура, при полный резонансе, при котором обобщенная расстройка равна нулю 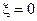 , и сопротивление связи равно оптимальному значению
, и сопротивление связи равно оптимальному значению 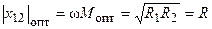 ,
,
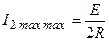 .
.
При индуктивной трансформаторной связи между контурами вблизи резонанса 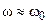 отношение сопротивления связи к сопротивлению потерь контура можно представить следующим приближённым выражением
отношение сопротивления связи к сопротивлению потерь контура можно представить следующим приближённым выражением
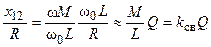 .
.
где 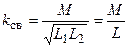 — коэффициент связи между индуктивностями контуров.
— коэффициент связи между индуктивностями контуров.
Определим нормированную АЧХ связанных контуров, используя в качестве нормирующего значения максимальное значение тока вторичного контура при полном резонансе,
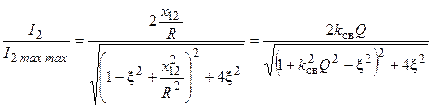 . (13.3)
. (13.3)
Максимумы AЧХ (13.3) имеют место при минимальных значениях знаменателя этой функции. Для определения значений расстройки, соответствующих минимумам знаменателя необходимо решить следующее уравнение
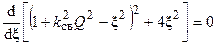
Вычислив первую производную, получим кубическое уравнение:
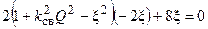 ;
;
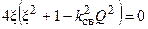 ,
,
которое имеет три корня:
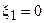 ;
; 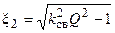 ;
; 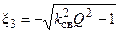 .
.
Корень 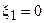 соответствует резонансу на частоте
соответствует резонансу на частоте 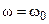 . Два остальных корня имеют физический смысл только при выполнении условия
. Два остальных корня имеют физический смысл только при выполнении условия 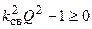 , которое можно записать в виде
, которое можно записать в виде
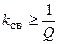 .
.
Значение коэффициента связи, при котором данное неравенство превращается в равенство, называют критическим коэффициентом связи 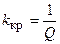 .
.
Частотные характеристики связанных колебательных контуров при различных коэффициентах связи показаны на рис. 13.3.
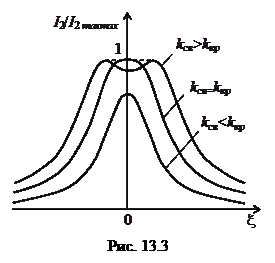 При коэффициенте связи меньше критического
При коэффициенте связи меньше критического 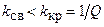 (слабая связь) АЧХ связанных контуров имеет вид одногорбой кривой, максимумом которой имеет место при
(слабая связь) АЧХ связанных контуров имеет вид одногорбой кривой, максимумом которой имеет место при 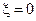 , то есть на резонансной частоте
, то есть на резонансной частоте 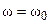 (), и равен
(), и равен
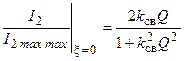 .
.
Поскольку произведение 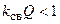 , то максимум нормированной АЧХ при слабой связи меньше единицы.
, то максимум нормированной АЧХ при слабой связи меньше единицы.
При коэффициенте связи, равном критическому 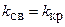 (критическая связь) произведение
(критическая связь) произведение 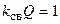 . При этом АЧХ также одногорбая с максимальным значение, равным единице.
. При этом АЧХ также одногорбая с максимальным значение, равным единице.
При коэффициенте связи больше критического 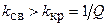 (сильная связь) АЧХ связанных контуров становится двугорбой кривой, имеющей два максимума и один минимум. Максимумы АЧХ соответствуют значениям обобщённой расстройки
(сильная связь) АЧХ связанных контуров становится двугорбой кривой, имеющей два максимума и один минимум. Максимумы АЧХ соответствуют значениям обобщённой расстройки 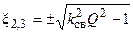 , то есть частотам, одна из которых больше резонансной частоты
, то есть частотам, одна из которых больше резонансной частоты 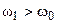 , а другая меньше
, а другая меньше 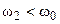 . Минимум АЧХ соответствует нулевой обобщённой расстройке
. Минимум АЧХ соответствует нулевой обобщённой расстройке 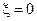 , то есть непосредственно резонансной частоте
, то есть непосредственно резонансной частоте 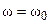 , и его значение уменьшается при увеличении коэффициента связи, поскольку произведение
, и его значение уменьшается при увеличении коэффициента связи, поскольку произведение 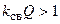 .
.
С физической точки зрения наличие при сильной связи двух максимумов АЧХ на частотах, отличающихся от резонансной, объясняется тем, что каждый из связанных контуров вносит в другой контур сопротивление реактивного характера, что вызывает взаимную расстройку контуров. Поскольку вносимые сопротивления пропорциональны коэффициенту связи, то его увеличение вызывает увеличение этих сопротивлений и, следовательно, увеличение взаимной расстройки контуров.
По сравнению с одиночными колебательными контурами, связанные контуры имеют нормированную АЧХ с большей крутизной склонов, что обеспечивает лучшую частотную избирательность. Кроме того, изменения коэффициента связи между контурами можно изменять их полосу пропускания, не изменяя средней частоты настройки. Поэтому связанные контура находят широкое применение в различных радиотехнических устройствах.
Определим полосу пропускания связанных контуров на уровне 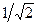 , с учётом которого составим уравнение, используя выражение для нормированной АЧХ (13.3),
, с учётом которого составим уравнение, используя выражение для нормированной АЧХ (13.3),
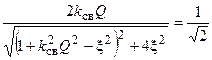 . (13.4)
. (13.4)
Преобразуем уравнение (14.4):
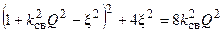 ;
;
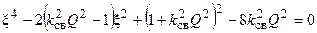 .
.
Делая замену переменной 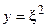 , получаем квадратное уравнение
, получаем квадратное уравнение
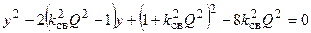 ,
,
решая которое, находим
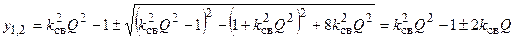 ,
,
которое имеет физический смысл, если только представляет собой положительное вещественное число. Такому условию удовлетворяет решение 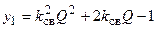 , учитывая которое, находим
, учитывая которое, находим
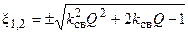 .
.
При критической связи 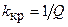 получаем значения обобщённой расстройки, соответствующие границам полосы пропускания
получаем значения обобщённой расстройки, соответствующие границам полосы пропускания 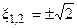 , которые в 1,41 раза больше аналогичных значений одиночного контура.
, которые в 1,41 раза больше аналогичных значений одиночного контура.
Заключение
Не смотря на то, что теория электрических цепей достаточно хорошо разработана, не исключена возможность появления новых методов анализа, синтеза и принципов построения цепей.
Наглядным подтверждением этому является быстрое развитие аналоговых активных фильтров на основе операционных усилителей, фильтров с переключаемыми конденсаторами цифровых фильтров и пр.
В настоящее время разработан ряд пакетов прикладных программ, которые позволяют по заданным типу фильтра (ФНЧ, ФВЧ, ПФ, ЗФ и т.п.), виду аппроксимации его АЧХ, порядку передаточной функции и требованиям к АЧХ синтезировать фильтр и моделировать его работу в частотной и временной областях. К таким программам относятся: Microwave Office, MicroCap, Filter Solutions, FilterPro и др. Поэтому расчет и оптимизацию фильтров выполняют, как правило, путем их моделирования на ЭВМ.
Широкое распространение в настоящее время получили цифровые фильтры, возможности которых практически зависят только от используемого программного обеспечения и быстродействия компьютера, которые постоянно прогрессируют. Например, с помощью цифровых фильтров можно получить практически полное подавление нежелательных частотных составляющих спектра обрабатываемого сигнала, что невозможно выполнить с помощью аналоговых фильтров. Кроме того, цифровые фильтры не вызывают фазовых сдвигов составляющих спектра обрабатываемого сигнала и не добавляют шум в выходной сигнал.
Однако история развития техники показывает, что во многих применениях простота и высокое быстродействие аналоговых устройств весьма эффективно дополняют универсальность и широкие функциональные возможности цифровых устройств.
Следует иметь в виду, что теория линейных электрических цепей, по существу, является частью общей теории линейных систем, которая в своем развитии использовала методы и принципы теоретической механики, теории автоматического регулирования и других наук. Поэтому рассмотренные выше методы анализа линейных цепей применимы для анализа линейных неэлектрических устройств и систем.
Что касается теории анализа и синтеза нелинейных электрических цепей, то это задача и методы ее решения находятся в стадии развития. Еще в большей степени это относится к теории нелинейных систем.
