Характеристики параллельного контура второго вида
Конструктивной особенностью параллельного контура второго вида является использование катушки индуктивности с отводом от части витков (рис. 12.8). При этом одна ветвь контура образована частью катушки с индуктивностью  , а другая ветвь — частью катушки с индуктивностью
, а другая ветвь — частью катушки с индуктивностью  вместе с конденсатором
вместе с конденсатором 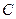 .
.
 Для такой цепи вводится понятие коэффициента включения индуктивности в виде отношение модуля комплексного сопротивления части индуктивности
Для такой цепи вводится понятие коэффициента включения индуктивности в виде отношение модуля комплексного сопротивления части индуктивности  к модулю комплексного сопротивления всей индуктивности
к модулю комплексного сопротивления всей индуктивности 
 .
.
Коэффициент включения может изменяться в пределах  . При
. При  параллельный контур второго вида вырождается в параллельный контур первого вида, а при
параллельный контур второго вида вырождается в параллельный контур первого вида, а при  — в последовательный контур.
— в последовательный контур.
С учётом коэффициента включения определим реактивные составляющие ветвей контура:
 ;
;
 .
.
Используя найденное ранее уравнение  , соответствующее условию резонанса токов, получаем
, соответствующее условию резонанса токов, получаем
 .
.
Решая уравнение, находим резонансную частоту параллельного контура второго вида  .
.
Видно, что частота резонансов токов не зависит от коэффициента включения индуктивности и совпадает с резонансной частотой контура первого вида, построенного из тех же элементов, что и рассматриваемый контур.
Поскольку полная индуктивность и сопротивления потерь контура не зависит от коэффициента включения, то максимальная энергия  , запасаемая в каждом из реактивных элементов, и энергия потерь
, запасаемая в каждом из реактивных элементов, и энергия потерь  в сопротивлении потерь за один период колебаний у контура второго вида будут такими же, как у контура первого вида. Следовательно, добротности этих контуров
в сопротивлении потерь за один период колебаний у контура второго вида будут такими же, как у контура первого вида. Следовательно, добротности этих контуров  с энергетической точки зрения будут также одинаковыми.
с энергетической точки зрения будут также одинаковыми.
Используя приближенную формулу для резонансной проводимости обобщённого параллельного контура  , определим резонансное сопротивление контура второго вида
, определим резонансное сопротивление контура второго вида
 ,
,
где  — эквивалентное сопротивление потерь контура.
— эквивалентное сопротивление потерь контура.
Таким образом, резонансное сопротивление контура с неполным включением индуктивности зависит от коэффициента включения  и значение этого сопротивления меньше резонансного сопротивления контура первого вида
и значение этого сопротивления меньше резонансного сопротивления контура первого вида  .
.
Зависимость резонансного сопротивления контура второго вида от коэффициента включения может быть использовано для согласования контура как с источником входного тока, так и с нагрузкой. Если источник тока и нагрузка имеют разные сопротивления, что обычно случается на практике, то каждого из них выбирают свой коэффициент включения, обеспечивающий согласованный режим работы по мощности.
В связи с тем, что одна из ветвей контура второго вида (рис. 12.8) представляет собой паразитный последовательный колебательный контур, состоящий из элементов  , то в параллельном контуре второго вида наряду с резонансом токов на частоте
, то в параллельном контуре второго вида наряду с резонансом токов на частоте  будет иметь место паразитный резонанс напряжений, условием которого является уравнение
будет иметь место паразитный резонанс напряжений, условием которого является уравнение  , решая которое находим вторую резонансную частоту
, решая которое находим вторую резонансную частоту
 ,
,
Частота паразитного резонанс больше частоты основного резонанса  . Поскольку на частоте паразитного резонанса сопротивление ветви контура, содержащей последовательный контур, равно сопротивлению
. Поскольку на частоте паразитного резонанса сопротивление ветви контура, содержащей последовательный контур, равно сопротивлению  , то очевидно, что модуль комплексного сопротивления контура на этой частоте будет меньше сопротивления
, то очевидно, что модуль комплексного сопротивления контура на этой частоте будет меньше сопротивления  , то есть
, то есть  .Так как
.Так как  , то следовательно
, то следовательно  .
.
 На рис. 12.9 показаны частотные зависимости модуля (рис. 12.9, а) и аргумента (рис. 12.9, б) комплексного сопротивления контура второго вида.
На рис. 12.9 показаны частотные зависимости модуля (рис. 12.9, а) и аргумента (рис. 12.9, б) комплексного сопротивления контура второго вида.
На частоте резонанса токов  сопротивление контура достигает максимального значения
сопротивление контура достигает максимального значения  и имеет резистивный характер. Из частотной зависимости аргумента комплексного сопротивления контура следует, что в диапазоне частот
и имеет резистивный характер. Из частотной зависимости аргумента комплексного сопротивления контура следует, что в диапазоне частот  сопротивление контура имеет резистивно-ёмкостной характер, а вне этого диапазона, то есть на частотах
сопротивление контура имеет резистивно-ёмкостной характер, а вне этого диапазона, то есть на частотах  и
и  , — резистивно-индуктивный характер.
, — резистивно-индуктивный характер.
Минимум модуля сопротивления контура имеет место на частоте паразитного резонанса  . Этот резонанс может быть использован для подавления составляющих входного тока контура, частота которых близких к частоте основного резонанса
. Этот резонанс может быть использован для подавления составляющих входного тока контура, частота которых близких к частоте основного резонанса  рассматриваемого контура.
рассматриваемого контура.
Приближенный анализ показывает, что нормированные АЧХ и ФЧХ контура второго вида совпадают с частотными зависимостями нормированного модуля и аргумента комплексного сопротивления этого контура.
