Линейный трансформатор без сердечника и его характеристики
Трансформатором называется устройство для передачи энергии из одной части электрической цепи в другую, действие которого основано на использовании явления взаимоиндукции.
Трансформатор как электрическое устройство относится к классу электрических машин и применяется для повышения или понижения амплитудных значений переменных напряжений и токов. С этой точки зрения различают повышающие и понижающие трансформаторы.
Конструктивно трансформатор состоит из двух или более индуктивно связанных катушек, называемых обмотками. Обмотки трансформатора обычно наматываются изолированным медным проводом на общем каркасе или безкаркасно одна на другую и разделяются диэлектрическими прокладками. После чего в каркас вставляется замкнутый ферромагнитный сердечник, что позволяет существенно уменьшить магнитный поток рассеяния трансформатора. Поскольку магнитная проницаемость ферромагнитных материалов зависит от напряженности магнитного поля, создаваемого в нём токами обмоток трансформатора, то в общем случае такой трансформатор является нелинейным устройством, и процессы в нём описываются нелинейным дифференциальным уравнением. К одной из обмоток трансформатора, которая называется первичной обмоткой, подключается источник переменного напряжения или тока. К остальным обмоткам, называемым вторичными обмотками, подключаются нагрузки.
Трансформатор без ферромагнитного сердечника является линейным, и процессы в нём описываются линейны дифференциальным уравнением.  Рассмотрим линейный трансформатор, который состоит из двух обмоток (рис. 9.6), включённых встречно, к первичной обмотке которого приложено гармоническое напряжение
Рассмотрим линейный трансформатор, который состоит из двух обмоток (рис. 9.6), включённых встречно, к первичной обмотке которого приложено гармоническое напряжение  . Это напряжение вызывает в первичной обмотке ток
. Это напряжение вызывает в первичной обмотке ток  . Часть потокосцепления, обусловленного током
. Часть потокосцепления, обусловленного током  , возбуждает во вторичной обмотке трансформатора э.д.с. взаимоиндукции
, возбуждает во вторичной обмотке трансформатора э.д.с. взаимоиндукции  . Если к вторичной обмотке подключенная нагрузка, то под действие э.д.с.
. Если к вторичной обмотке подключенная нагрузка, то под действие э.д.с.  в ней пойдет ток
в ней пойдет ток  . Последний вызывает своё потокосцепление, часть которого возбуждает в первичной обмотке э.д.с. взаимоиндукции
. Последний вызывает своё потокосцепление, часть которого возбуждает в первичной обмотке э.д.с. взаимоиндукции  .
.
Тогда уравнения трансформатора, составленные в комплексной форме по второму закону Кирхгофа, будет иметь вид:

где  ,
,  — индуктивности обмоток трансформатора;
— индуктивности обмоток трансформатора;  и
и  — сопротивления, учитывающие потери энергии в обмотках трансформатора.
— сопротивления, учитывающие потери энергии в обмотках трансформатора.
Полученные уравнения равносильны следующим:

Если токи  и
и  рассматривать как контурные токи контуров, образованных обмотками трансформатора и подключёнными к ним элементами, то в соответствии с уравнениями можно составить эквивалентную схему замещения трансформатора, в которой обмотки трансформатора связаны не индуктивно, а электрически (кондуктивно) (рис. 9.7).
рассматривать как контурные токи контуров, образованных обмотками трансформатора и подключёнными к ним элементами, то в соответствии с уравнениями можно составить эквивалентную схему замещения трансформатора, в которой обмотки трансформатора связаны не индуктивно, а электрически (кондуктивно) (рис. 9.7).
В режим холостого хода, то есть при отсутствии нагрузки, ток вторичной обмотки трансформатора равен нулю  . При этом ток первичной обмотки трансформатора будет равен
. При этом ток первичной обмотки трансформатора будет равен
 .
.

Рис. 9.7
Найденное значение тока называется током намагничивания или током холостого хода, трансформатора.
Если первичная обмотка подключена источнику напряжения, близкому к идеальному, то действующие значения напряжения на обмотках трансформатора практически остаются такими же, какими они были в режиме холостого хода. Возникновение тока вторичной обмотки трансформатора вызывает увеличение тока первичной обмотке, что приводи к увеличению мощности, потребляемой трансформатором от источника напряжения. Изменение тока вторичной обмотки приводит к пропорциональному изменению тока первичной обмотки, а также мощности, потребляемой от источника напряжения.
Определим входное сопротивление трансформатора, вторичная обмотка которого нагружена комплексным сопротивление  . Поскольку напряжение на нагрузке
. Поскольку напряжение на нагрузке  , то уравнения трансформатора можно записать в виде:
, то уравнения трансформатора можно записать в виде:

Решая второе уравнение относительно тока вторичной обмотки

и подставляя найденное выражение в первое уравнение, находим входное сопротивление трансформатора

где  — вносимым сопротивление из цепи вторичной обмотки в цепь первичной обмотки.
— вносимым сопротивление из цепи вторичной обмотки в цепь первичной обмотки.
Трансформатор, у которого ток намагничивания равен нулю, что возможно только при условии  , называется идеальным трансформатором, и его уравнения имеют вид:
, называется идеальным трансформатором, и его уравнения имеют вид:
 ;
;
 ,
,
где  — коэффициент трансформации, равный отношению числа витков обмоток.
— коэффициент трансформации, равный отношению числа витков обмоток.
Трансформатор, у которого  (
(  ) и, называется повышающим, а трансформатор, у которого
) и, называется повышающим, а трансформатор, у которого  (
(  ) — понижающим.
) — понижающим.
Поскольку коэффициент трансформации 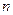 является действительным числом, то напряжение и ток вторичной обмотки идеального трансформатора имеют такие же начальные и мгновенные фазы, как соответствующие напряжения и ток первичной обмотки и отличаются от них только по амплитуде. Коэффициент полезного действия такого трансформатора равен единице.
является действительным числом, то напряжение и ток вторичной обмотки идеального трансформатора имеют такие же начальные и мгновенные фазы, как соответствующие напряжения и ток первичной обмотки и отличаются от них только по амплитуде. Коэффициент полезного действия такого трансформатора равен единице.
Если потери мощности непосредственно в трансформаторе достаточно малы, то можно приближенно его рассматривать как идеальный. В этом случае мощности в первичной и вторичной обмотках трансформатора одинаковы  и можно считать, что действующие значения токов в обмотках трансформатора приблизительно обратно пропорциональны действующим значениям напряжениям
и можно считать, что действующие значения токов в обмотках трансформатора приблизительно обратно пропорциональны действующим значениям напряжениям
 .
.
Если к выводам вторичной обмотки идеального трансформатора подключить сопротивление нагрузки  , то входное сопротивление идеального трансформатора со стороны первичной обмотки будет равно
, то входное сопротивление идеального трансформатора со стороны первичной обмотки будет равно
 .
.
Отсюда следует, что входное сопротивление идеального трансформатора имеет такой же характер, как и сопротивление нагрузки и отличается от него только по модулю в  раз.
раз.
Если первичная обмотка подключена источнику напряжения, близкому к идеальному, то действующие значения напряжений на обмотках трансформатора практически остаются неизменными при различных токах этих обмоток. При подключении ко вторичной обмотке трансформатора сопротивления нагрузки в этой обмотке возникает ток, который увеличивается при уменьшении сопротивления нагрузки, приводит к пропорциональному увеличению мощности, потребляемой нагрузкой. При этом ток первичной обмотки трансформатора также увеличивается пропорционально току нагрузки, что приводит к увеличению мощности, потребляемой трансформатором от источника напряжения.
В реальном трансформаторе, в отличие от идеального, имеют место потери энергии, а также запасание энергии в электрическом поле паразитных емкостей. Кроме того, индуктивность обмоток реального трансформатора имеет конечное значение, а потокосцепления рассеяния не равны нулю. Поэтому при разработке конструкции трансформатора принимаются меры, направленные на приближение его свойств к свойствам идеального трансформатора.
Несмотря на то, что реальный трансформатор по своим свойствам отличается от идеального, аналитические выражения, полученные для идеального трансформатора, широко используются при расчете реальных трансформаторов.
