Коэффициент связи между катушками индуктивности
Коэффициент связи между катушками индуктивности определяется как среднее геометрическое отношений, которые показывают, какая часть магнитного потока самоиндукции одной катушки проходит через витки другой катушки,
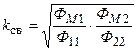 .
.
Отсюда следует, что значение коэффициента связи удовлетворяет условию
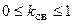 .
.
При 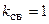 поток самоиндукции одной из катушек полностью проходит через витки другой катушки, что обеспечивает максимальную магнитную связь между катушками. При
поток самоиндукции одной из катушек полностью проходит через витки другой катушки, что обеспечивает максимальную магнитную связь между катушками. При 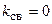 магнитная связь между катушками отсутствует.
магнитная связь между катушками отсутствует.
Зависимость составляющих потокосцепления индуктивно связанных катушек с токами, числом витков, собственными и взаимными индуктивностями выражается следующими уравнениями:
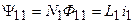 ;
;
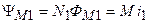 ;
;
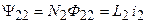 ;
;
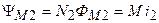 .
.
Решив эти уравнения относительно магнитных потоков и подставив их в выражение для коэффициента связи, получим
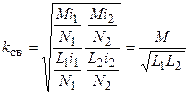 ,
,
Откуда
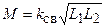 .
.
С учётом возможных значений коэффициента связи определяем пределы изменения взаимной индуктивности
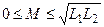 .
.
Очевидно, что максимальное значение взаимной индуктивности катушек не может превышать среднего геометрического значения их собственных индуктивностей.
9.4. Эквивалентное преобразование участков цепи, содержащих индуктивно
связанные катушки
Рассмотрим цепи, состоящей из последовательно соединённых индуктивно связанных катушек (рис. 9.4).
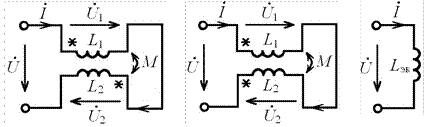
а) б) в)
Рис. 9.4
Полагая ток цепи равным 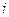 , определим в комплексной форме напряжение цепи при согласном включении катушек (рис. 9.4, а)
, определим в комплексной форме напряжение цепи при согласном включении катушек (рис. 9.4, а)
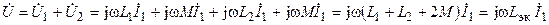
и при встречном включении катушек (рис. 9.4, б)
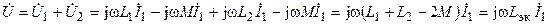 .
.
Из полученных соотношений следует, что эквивалентная индуктивность цепи определяется по формуле
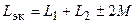 .
.
где знак «плюс» соответствует согласному включению катушек, а знак «минус» – встречному.
Тогда рассматриваемая цепь может быть заменена эквивалентной схемой, показанной на рис. 9.4, в).
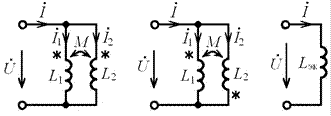
Рассмотрим цепи, состоящей из параллельно соединённых индуктивно связанных катушек (рис. 9.5).
а) б) в)
Рис. 9.5
При согласном включении катушек (рис. 9.5, а) напряжение, приложенное к цепи, может быть выражено через токи катушек в следующем виде:
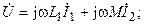
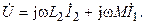
Решая втрое уравнение относительно тока второй катушки
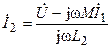 .
.
и подставляя полученное выражение в первое уравнение
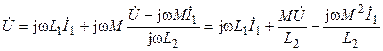 .
.
решая которое, находим
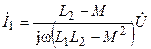 .
.
Аналогичным образом определяется ток второй катушки
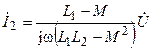 .
.
Определим входной ток цепи
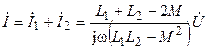 .
.
Тогда эквивалентное комплексное сопротивление цепи будет равно
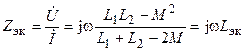 .
.
Аналогичным образом можно определить эквивалентное комплексное сопротивление цепи при встречном включении катушек (рис. 9.5, б)
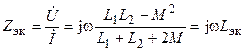 .
.
Из полученных соотношений следует, что эквивалентная индуктивность цепи (рис. 9.5, в) определяется по формуле
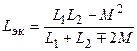 ,
,
в которой знак минус соответствует согласному, а знак плюс — встречному включению катушек.
Лекция № 11
