Комплексные схемы замещения источников напряжения и тока

Ранее были рассмотрены последовательные схемы замещения реальных источников постоянного тока и напряжения и получены соотношения для их взаимного преобразования.

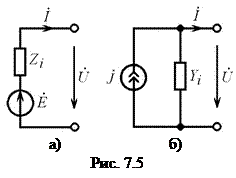Аналогичные соотношения справедливы и для реальных источников гармонического напряжения и тока. При этом комплексная схема замещения реального источника гармонического напряжения будет состоять из последовательно включённых идеального источника напряжения 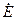и комплексного внутреннего сопротивления 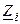(рис. 7.5, а), а комплексная схема замещения реального источника тока — из параллельно включённых идеального источника тока 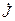и комплексной внутренней проводимости 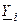(рис. 7.5, б). Обе схемы замещения эквивалентны друг другу при выполнении следующих условий:

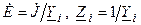
или

.

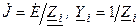Если анализируемая цепь содержит идеальный источник напряжения, последовательно с которым включён любой пассивный элемент, то, принимая комплексное сопротивление этого элемента за внутреннее сопротивлением источника напряжения (рис. 7.5, а) и используя приведенные выше формулы, можно преобразовать источник напряжения в эквивалентный ему источник тока.

Аналогично, если анализируемая цепь содержит идеальным источником тока, параллельно которому включен любой пассивный элемент, то, принимая комплексную проводимость этого элемента за внутреннюю проводимость источника тока (рис. 7.5, б) и используя приведенные выше формулы, можно преобразовать источник тока в эквивалентный ему источник напряжения.

Тема 8. Методы расчёта сложных электрических цепей

Метод контурных токов

Метод контурных токов основан на том, что вместо токов ветвей электрической цепи определяются так называемые контурные токи, которые замыкаются в независимых контурах анализируемой цепи. Используя контурные токи, составляются уравнения равновесия цепи на основании второго закона Кирхгофа, которые называются контурными уравнениями. Решая эти уравнения, определяются контурные токи и затем рассчитываются токи и напряжения ветвей и элементов цепи.

Ранее было установлено, что число независимых контуров электрической цепи определяется числом 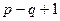главных ветвей цепи. Следовательно, для определения контурных токов достаточно составить систему из 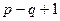уравнений, используя второй закон Кирхгофа. Направления контурных токов могут быть выбраны произвольно. Однако направление обхода каждого контура обычно выбирают, совпадающим с направлением контурного тока этого контура.

Рассмотрим методику составления контурных уравнений на примере цепи, показанной на рис. 8.1, а, которая содержит шесть ветвей 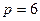и четыре узла .

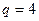На рис. 8.1, б изображен граф цепи, дерево которого, состоит из ветвей 4, 5 и 6, выделенных жирными линиями. Из структуры дерева видно, что главными ветвями графа являются ветви 1, 2 и 3. Следовательно, цепь содержит три независимых контура.

Условимся сумму сопротивлений ветвей, входящих в рассматриваемый контур называть собственным сопротивлениемэтогоконтура, а сумму сопротивлений, общих для данного контура и смежного с ним контура взаимным сопротивлениемконтуров.

Для рассматриваемой цепи собственное сопротивление первого контура равно 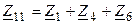, второго контура — 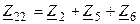и третьего — 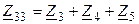. Соответственно взаимным сопротивлением первого и второго контуров равно 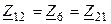, первого и третьего контуров — 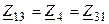и второго и третьего контуров — .

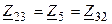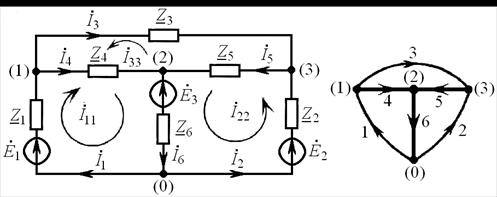
а) б)

Рис. 8.1

При составлении контурного уравнения по второму закону Кирхгофа падение напряжения на собственном сопротивлении контура, обусловленное контурным током данного контура, записываются в левой части уравнения со знаком «плюс». Падение напряжения на взаимном сопротивлении, обусловленное током смежного контура, записывается также в левой части уравнения со знаком «плюс», если контурные токи смежных контуров направлены во взаимном сопротивлении одинаково, и со знаком «минус», если эти тока направлены встречно.

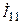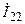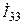Выбираем направления контурных токи , и , пути протекания которых обозначена закруглённой стрелкой (рис. 8.1, а). Поскольку каждый контурный ток замыкаются в контуре, образованным одной из главных ветвей и ветвями дерева (рис. 8.1, б), то эти токи являются токами главных ветвей 1, 2 и 3, то есть 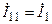, 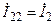и .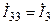

Если рассматриваемый контур содержит идеализированные источники напряжения, то э.д.с. каждого такого источника записывают в правой части контурного уравнения со знаком «плюс», если её направление совпадает с направлением контурного тока, и со знаком «минус», если её направление противоположно направлению контурного тока. В результате, правая часть контурного уравнения представляет собой алгебраическую сумму э.д.с. идеализированных источников напряжения, входящих в контур. Такая сумма называетсяконтурной э.д.с. Если контур не содержит источников напряжения, то его контурная э.д.с. равна нулю.

Для цепи (рис. 8.1) контурная э.д.с. первого контура равна 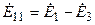, второго контура — 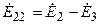и третьего контура — .

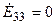На основании выше изложенного можно сформулировать следующее правило составления контурного уравнения: левая часть контурного уравнения составляется в виде алгебраической суммы произведения контурного тока на собственное сопротивление контура и произведений контурных токов смежных контуров на их взаимные сопротивления с данным контуром, а его правая часть — в виде контурной э.д.с.

Используя указанное правило, составляем систему контурных уравнений цепи (рис. 8.1, а):

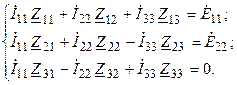
Решая систему уравнений, находят контурные токи, зная которые рассчитывают токи и напряжения ветвей и элементов цепи. Например, ток четвёртой ветви будет равен 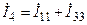и т.д.

Обобщая полученную ранее систему контурных уравнений на случай, когда электрическая цепь имеет 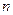независимых контуров, получаем:

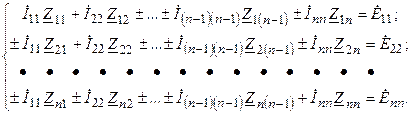
Решение системы уравнений относительно k-го контурного тока может быть найдено с помощью определителей

,

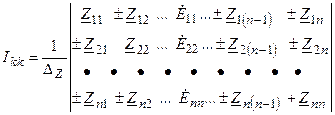где

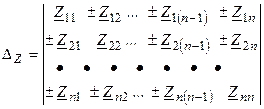
— определитель системы с индексом «Z», который означает, что членами определителя являются комплексные сопротивления.

Дальнейшее преобразование k-го контурного тока осуществляется согласно правилу разложения определителя по элементам k-го столбца.

Если в состав цепи входят ветви, содержащие источник тока, то дерево графа целесообразно выбирать так, чтобы такие ветви являлись главными ветвями графа, а, значит входили в состав независимых контуров. Поскольку контурный ток контура, содержащего ветвь с источником тока, будет равен току этого источник, то такой контурный ток становится известной величиной. 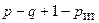В результате, число необходимых контурных уравнений уменьшается до значения , где 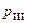— число главных ветвей содержащих источник тока.

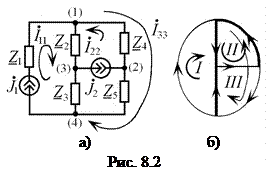
В качестве примера рассмотрим цепь, изображенную на рис. 8.2, а. С учётом указанных выше рекомендациями построим граф цепи (рис. 8.2, б), две главные ветви которого содержащие источники тока 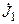и .

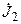В результате, контурные токи первого и второго независимых контуров (рис.8.2, б) являются известными величинам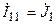и: и 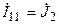. Тогда для определения третьего контурного тока 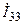достаточно составить только одно уравнение

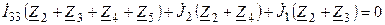
Решая уравнения, находим неизвестный контурный ток, и затем рассчитываем токи и напряжения ветвей и элементов цепи.

Лекция № 9

Метод узловых напряжений

Метод узловых напряжений основан на определении напряжений узлов цепи относительно некоторого базисного узла. Искомые напряжения узлов называются узловыми напряжениями, используя которые составляются уравнения по первому закону Кирхгофа, называемые узловыми уравнениями. Решая систему узловых уравнений, находят узловые напряжения, и затем рассчитать напряжения и токи ветвей и элементов электрической ветви.

Базисный узел часто называют нулевым узлом, поскольку его потенциал условно может быть принят равным нулю. Тогда напряжение между рассматриваемым узлом и базисным будут равны потенциалу рассматриваемого узла. Поэтому данный метод называют также методом узловых потенциалов. В качестве базисного узла целесообразно выбирать узел, в котором сходится наибольшее число ветвей.

За положительное направление узлового напряжения узла принимают направление от рассматриваемого узла к базисному узлу. Число узловых уравнений определяется числом независимых узлов цепи .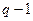

Рассмотрим метод составления узловых уравнений на примере цепи, показанной на рис. 8.3. В качестве базисного выбираем узел, в котором сходится 5 ветвей. Тогда узловое напряжение первого узла равно 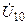, второго — 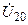и третьего — .

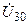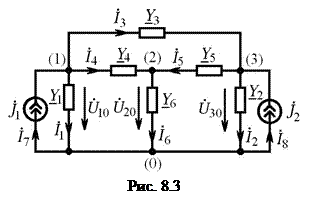Поскольку общее число узлов цепи (рис. 8.3) 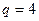, то для её расчета по методу узловых напряжений необходимо составить 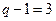узловых уравнения по первому закону Кирхгофа.

Условимся сумму проводимостей ветвей, подключенных к рассматриваемому узлу, называть собственной проводимостьюузла, а сумму проводимости ветвей, включенных непосредственно между двумя смежными узлами —взаимной проводимостью между узлами. Для цепи (рис. 8.3) собственная проводимость первого узла равна 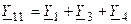, второго узла — 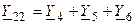и третьего узла — 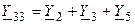. Соответственно взаимная проводимость между первым и вторым узлом равна 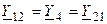, между первым и третьим — 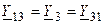и между вторым и третьим — .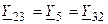

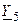При составлении узловых уравнений по первому закону Кирхгофа электрический тока, вызываемый в собственной проводимости узла его узловым напряжением, записывается в левой части уравнения со знаком «плюс», а электрический ток, вызываемый во взаимной проводимости узловым напряжением смежного узла, записывается в той же части уравнения, но со знаком «минус».

Если ветвь, подключённая к рассматриваемому узлу, содержит источник тока, то ток этого источника записывается в правой части узлового уравнения со знаком «плюс», если он направлен к узлу, и со знаком «минус», если он направлен от узла. В результате, правая часть узлового уравнения представляет собой алгебраическую сумма токов источников тока, входящих в состав ветвей, подключенных к данному узлу. Такая сумма называетсяузловым током. Если ветви, подключенные к данному узлу, не содержит источников тока, то узловой ток этого узхла равен нулю.

Для цепи (рис. 8.3) узловой ток первого узла равен 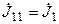, второго — 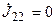, третьего — .

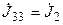На основании выше изложенного можно сформулировать следующее правило составления узлового уравнения: левая часть узлового уравнения должна представлять собой сумму произведения узлового напряжения на собственную проводимость узла и произведений узловых напряжений соседних узлов на соответствующие им взаимные проводимости, взятых со знаком «минус», а его правая часть должна представлять собой узловой ток.

Используя указанное правило, составляем систему узловых уравнений электрической цепи (рис. 8.3):

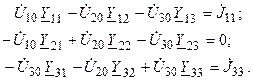
Решая систему уравнения, находят узловые напряжения, и затем рассчитывают напряжения и токи ветвей и элементов цепи. Например, напряжения на проводимостях 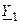, 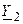и 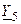соответственно равны узловым напряжениям 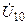, 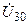и 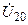, напряжение на проводимости 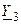равно 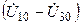, на проводимости 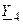— 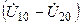и на проводимости — .

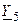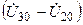Обобщая полученную ранее систему узловых уравнений на случай, когда электрическая цепь имеет 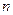независимых узлов, получаем:

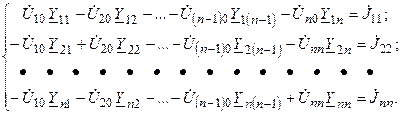
Решение системы уравнений относительно k-го узлового напряжения может быть найдено с помощью определителей

,

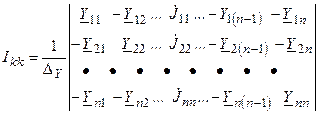где

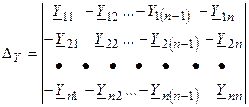
— определитель системы с индексом «Y», который означает, что членами определителя являются комплексные проводимости.

Дальнейшее преобразование k-го узлового напряжения осуществляется согласно правилу разложения определителя по элементам k-го столбца.

Если между двумя какими-либо узлами цепи включен идеальный источник напряжения, то один из таких узлов целесообразно принять за базисный (нулевой) узел. Тогда напряжение другого узла, к которому подключён идеального источника напряжения, будет равно э.д.с. источника, то есть станет известной величиной. В результате, число составляемых уравнений, уменьшается до значения 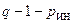, где 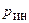— число идеальных источников напряжения, включённых между базисным узлом и другими узлами цепи.

Если цепь содержит неидеальные источники напряжения, то перед составлением уравнений рекомендуется преобразовать их в эквивалентные источники тока по известным правилам (см. п. 7.4).

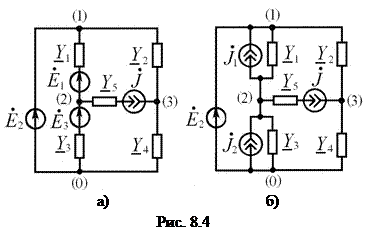
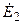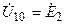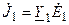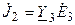Рассмотрим цепь (рис. 8.4, а), содержащую один идеальный источники напряжения , включенный между узлами 0 и 1. Если узел 0 принять за базисный узел, то узловое напряжение первого узла будет равно , то есть является известной величиной. Ветви, содержащие неидеальные источники напряжения, заменяем эквивалентными источниками тока . И . В результате, получаем эквивалентную схему замещения (8.4, б), для расчёта которой достаточно составить только два узловых уравнения:

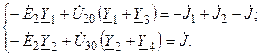
Решая систему уравнений, находят узловые напряжения 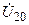и 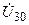, и затем рассчитывают напряжения и токи ветвей и элементов цепи.

Метод наложения

Метод наложения основан на принципе суперпозиции, согласно которому реакция линейной электрической цепей на сложное внешнее воздействие, которое может быть представлено в виде суммы более простых воздействий, равна сумме реакций, вызванных каждым из простых воздействий, действующих по отдельности.

В соответствии с методом наложения ток любой ветви электрической цепи может быть найден следующим образом.

1. Составляются эквивалентные схемы цепи, содержащие только один источник энергии, путем исключения всех остальных источников. При исключении идеального источника напряжения точки подключения этого источника замыкают накоротко. При исключении идеального источника тока ветвь, в которую он был включен, разрывают, то есть такая ветвь может быть исключена из эквивалентной схемы. При исключении источника напряжения или тока, имеющего конечное внутреннее сопротивление, последнее оставляют в эквивалентной схеме.

2. Для каждой эквивалентной схемы определяют ток интересующей нас ветви, создаваемый оставленным источником энергии. Такой ток называют частичным.

3. Находят полный ток интересующей нас ветви в виде алгебраической суммы частичных токов с учетом их направления, определяющего знак тока.

В качестве примера рассмотрим цепь (рис. 8.5, а), содержащую два источника электрической энергии.

а) б) в)

Рис. 8.5

Определим методом наложения ток 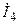, протекающий в ветви с сопротивлением 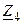. Составляем эквивалентные схемы исходной цепи, каждая из которых содержит только один источник электрической энергии (рис. 8.5, б, рис.8.5, в).

Используя эквивалентную схему (рис. 8.5, б), определяем частичный ток сопротивления 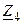, создаваемый источником напряжения ,

.

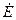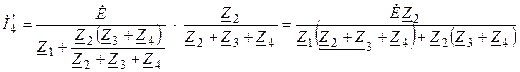Используя эквивалентную схему (рис. 8.5, в), определяем частичный ток сопротивления 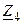, создаваемый источником тока ,

.

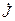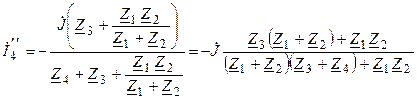Тогда полный ток 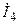, протекающий в сопротивлении 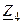при одновременном воздействии двух источников электрической энергии, определяется как алгебраическая сумма частичных токов

.
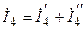