Расчет параметров цифрового частотного дискриминатора
Основной особенностью цифрового частотного дискриминатора (ЦЧД), реализующего обработку бинарно-квантованных сигналов в режиме работы «скользящее» окно, является возможность достаточно простого управления крутизной дискриминационной характеристики (ДХ) [1].
На рис. 18 представлен пример ДХ ЦЧД.
 |
| Рис. 18. Идеальная (прямая) и реальная (ступенчатая) дискриминационные характеристики |
Расчет параметров цифрового частотного дискриминатора (ЦЧД), осуществляется по следующим выражениям.
Крутизна дискриминационной характеристики (ДХ)  (В/Гц) определяется из следующего выражения
(В/Гц) определяется из следующего выражения
 (3.1)
(3.1)
где  (В/Гц) – коэффициент, характеризующий крутизну ДХ;
(В/Гц) – коэффициент, характеризующий крутизну ДХ;  (В) – величина напряжения, приходящаяся на один разряд;
(В) – величина напряжения, приходящаяся на один разряд;  (Гц) – вес одного разряда;
(Гц) – вес одного разряда;  (Гц) – половина ширины раскрыва ДХ ЦЧД, определяемая емкостью реверсивного счетчика;
(Гц) – половина ширины раскрыва ДХ ЦЧД, определяемая емкостью реверсивного счетчика;  (Гц) – разность частот между частотой входного сигнала
(Гц) – разность частот между частотой входного сигнала 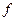 и опорной частотой;
и опорной частотой;  – величина, определяющая количество состояний реверсивного счетчика;
– величина, определяющая количество состояний реверсивного счетчика; 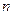 – величина, определяющая количество разрядов реверсивного счетчика.
– величина, определяющая количество разрядов реверсивного счетчика.
Максимальное напряжение  (В) на выходе ДХ ЦЧД определяется в соответствии с выражением
(В) на выходе ДХ ЦЧД определяется в соответствии с выражением
 (В),
(В),
откуда
 (В). (3.2)
(В). (3.2)
Как известно, точное значение той или иной частоты соответствует середине интервала  (Гц). Очевидно, что нахождение частоты в любой точке частотной оси, соответствующей весу того или иного разряда, равновероятно. Отсюда, выражение для плотности распределения вероятностей ошибки определения частоты внутри одного разряда, будет
(Гц). Очевидно, что нахождение частоты в любой точке частотной оси, соответствующей весу того или иного разряда, равновероятно. Отсюда, выражение для плотности распределения вероятностей ошибки определения частоты внутри одного разряда, будет
 .
.
Учитывая то обстоятельство, что математическое ожидание равно нулю, а критерием точности является среднеквадратическая величина
 (Гц),
(Гц),
где  – дисперсия частоты, то имеем
– дисперсия частоты, то имеем
 (Гц). (3.3)
(Гц). (3.3)
Относительная погрешность измерения
 . (3.4)
. (3.4)
Относительная погрешность  (%) будет минимальна при
(%) будет минимальна при  (Гц) и будет увеличивается по мере приближения входной частоты к опорной.
(Гц) и будет увеличивается по мере приближения входной частоты к опорной.
Абсолютное значение погрешности измерения  (Гц) зависит от диапазона анализа
(Гц) зависит от диапазона анализа  (Гц) и числа разрядов
(Гц) и числа разрядов 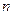 .
.
Максимальная величина диапазона (раскрыва ДХ) будет
 (Гц),
(Гц),
откуда
 (Гц). (3.5)
(Гц). (3.5)
Пример 11. Рассчитать крутизну ДХ  (В/Гц) ЦЧД, определить вес одного разряда
(В/Гц) ЦЧД, определить вес одного разряда  (Гц), среднеквадратическую погрешность
(Гц), среднеквадратическую погрешность  (Гц), и относительную погрешность
(Гц), и относительную погрешность  (%) для двух значений максимальной частоты линейного участка ДХ
(%) для двух значений максимальной частоты линейного участка ДХ  (Гц) и
(Гц) и  (Гц). Полагаем, что число разрядов реверсивного счетчика
(Гц). Полагаем, что число разрядов реверсивного счетчика  , а максимальное выходное напряжение
, а максимальное выходное напряжение  (В).
(В).
Определим количество состояний реверсивного счетчика
 .
.
Определим, используя (3.2), величину
 .
.
Определим, используя (3.5), величины веса одного разряда  и
и 
 (Гц);
(Гц);
 (Гц).
(Гц).
Крутизна ДХ 
 с учетом (3.1) будет
с учетом (3.1) будет
 (В/Гц)=199,885(мкВ/Гц);
(В/Гц)=199,885(мкВ/Гц);
 (В/Гц)=333,151(мкВ/Гц).
(В/Гц)=333,151(мкВ/Гц).
С учетом (3.3), величины среднеквадратической погреш-ности  будут
будут


Относительная  погрешность, с учетом (3.4), будет
погрешность, с учетом (3.4), будет
 ;
;
 .
.
Аналогичным образом решаются все задачи в п.10.1.9. в [2].
ЦИФРОАНАЛОГОВОЕ ПРЕОБРАЗОВАНИЕ СИГНАЛОВ
После цифровой обработки сигналов в соответствии с тем или иным алгоритмом, как правило, полученный результат преобразуют в аналоговую форму для дальнейшего использования. При этом на выходе устройства, осуществляющего подобные преобразования и называемого цифроаналоговым преобразователем (ЦАП), если не предпринимать каких-либо действий, будет последовательность ступенчатых отсчетов.
Известно, что одиночный сигнал прямоугольной формы длительности 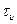 имеет спектральную плотность, огибающая которой описывается функцией вида
имеет спектральную плотность, огибающая которой описывается функцией вида 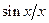 вдоль частотной оси. Эта функция обращается в нуль на оси абсцисс в точках
вдоль частотной оси. Эта функция обращается в нуль на оси абсцисс в точках  или
или  , где
, где  Между этими точками располагаются боковые лепестки (БЛ). При этом уровень первого БЛ нормированной по амплитуде спектральной плотности равен 0,2122 от максимального значения, равного единице, и располагается на частоте
Между этими точками располагаются боковые лепестки (БЛ). При этом уровень первого БЛ нормированной по амплитуде спектральной плотности равен 0,2122 от максимального значения, равного единице, и располагается на частоте 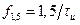 или
или  , т.е. в середине между точками
, т.е. в середине между точками 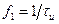 или
или  и
и 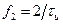 или
или 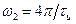 на частотной оси. Уровень второго БЛ равен 0,1273, т.е. примерно в 2 раза меньше чем первый БЛ и располагается на частоте
на частотной оси. Уровень второго БЛ равен 0,1273, т.е. примерно в 2 раза меньше чем первый БЛ и располагается на частоте  или
или  , т.е. в середине между точками
, т.е. в середине между точками  или
или  и
и 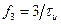 или
или  на частотной оси. Уровень каждого следующего БЛ уменьшается примерно в 2 раза при увеличении номера БЛ на единицу.
на частотной оси. Уровень каждого следующего БЛ уменьшается примерно в 2 раза при увеличении номера БЛ на единицу.
Известно, что сигнал, поступающий на цифровую обработку, подвергается дискретизации перед квантованием. При этом моменты времени появления сигнала, как и его окончания, в интервалах между выборками случайны. Они могут находиться в любой точке на временной оси между выборками. Следовательно, плотности распределения вероятностей момента времени появления и момента времени окончания сигнала между выборками могут быть приняты равновероятными. В этом случае математическое ожидание момента времени начала сигнала и момента времени его окончания равно середине временного интервала между выборками.
Отсюда следует, что если задано количество отсчетов 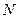 сигнала, взятых с периодом повторения
сигнала, взятых с периодом повторения 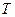 , то длительность аналогового сигнала
, то длительность аналогового сигнала 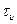 будет определяться соотношением
будет определяться соотношением
 (с). (4.1)
(с). (4.1)
При этом предполагается, что сигнал имеет прямоугольную форму огибающей во времени.
